Что такое «магические числа» в компьютерном программировании?
когда люди говорят об использовании «магических чисел» в компьютерном программировании, что они имеют в виду?
11 ответов
магические числа-это любое число в вашем коде, которое не сразу очевидно для кого-то с очень небольшим знанием.
например, следующий фрагмент кода:
магическое число в нем и было бы гораздо лучше написать так:
однако, хотя я знаю есть 1440 минут в день, я бы, наверное еще использовать MINS_PER_DAY идентификатор, так как это делает поиск их намного проще. Чей сказать, что приращение емкости, упомянутое выше, также не будет 1440, и вы в конечном итоге измените неправильное значение? Это особенно верно для низких чисел: шанс двойного использования 37197 относительно низок, шанс использование 5 для нескольких вещей довольно высоко.
использование идентификатора означает, что вам не придется проходить через все ваши исходные файлы 700 и изменять 729 to 730 когда увеличение емкости изменилось. Вы можете просто изменить одну строку:
и перекомпилировать много.
сравните это с магическими константами, которые являются результатом наивных людей, думающих, что только потому, что они удаляют фактическое номера из их кода, они могут меняться:
это добавляет абсолютно ноль дополнительная информация к вашему коду и является полной тратой времени.
предполагая, что вы не знали, что в году 365 дней, вы найдете это утверждение бессмысленным. Таким образом, хорошей практикой является присвоение всех «магических» чисел (чисел, которые имеют какое-то значение в вашей программе) константе,
и с тех пор сравните с этим. Это легче читать, и если земля когда-нибудь выйдет из строя, и мы получим дополнительный день. вы может легко изменить его (другие номера могут быть более вероятно, чтобы изменить).
другой вид магического числа, однако, используется в форматах файлов. Это просто значение, включенное, как правило, в первую очередь в файл, который помогает определить формат файла, версия формата файла и / или конечность конкретного файла.
например, у вас может быть магическое число 0x12345678. Если вы видите это магическое число, это справедливое предположение, что вы видите файл правильного формата. Если вы видите, с другой стороны, 0x78563412, это справедливое предположение, что вы видите эндианскую версию того же формата файла.
большинство ответов до сих пор описывали магическое число как константу, которая не является самоописанием. Будучи немного» старомодным » программистом, еще в те дни мы описывали магические числа как любую константу, которой назначается какая-то особая цель, которая влияет на поведение кода. Например, число 999999 или MAX_INT или что-то еще совершенно произвольное.
большая проблема с магическими числами заключается в том, что их цель может быть легко забыто, или значение, используемое в другом совершенно разумном контексте.
в качестве грубого и ужасно надуманного примера:
тот факт, что константа используется или не называется, на самом деле не проблема. В случае моего ужасного примера ценность влияет на поведение, но что, если нам нужно изменить значение «я» во время цикла?
очевидно, в приведенном выше примере, вам не нужно магическое число для выхода из цикла. Вы можете заменить его инструкцией break, и это реальная проблема с магическими числами, что они являются ленивым подходом к кодированию и в обязательном порядке всегда могут быть заменены чем-то менее склонным к сбою или к потере смысла с течением времени.
все, что не имеет очевидного значения для кого-либо, кроме самого приложения.
магические числа-это специальное значение определенных переменных, которое заставляет программу вести себя особым образом.
например, библиотека связи может принимать параметр тайм-аута, и он может определить магическое число «-1» для указания бесконечного тайм-аута.
термин магическое число обычно используется для описания некоторой числовой константы в коде. Число появляется без какого-либо дальнейшего описания, и поэтому его значение эзотерическое.
использование магических чисел можно избежать, используя именованные константы.
использование чисел в вычислениях, отличных от 0 или 1, которые не определены каким-либо идентификатором или переменной (что не только упрощает изменение числа в нескольких местах, изменяя его в одном месте, но и дает читателю понять, для чего это число).
в простых и истинных словах магическое число-это трехзначное число, сумма квадратов первых двух цифр которого равна третьей. Ex-202, как, 2*2 + 0*0 = 2*2. Теперь WAP в java принимает целое число и печатает, является ли это магическим числом или нет.
Это может показаться немного банальным, но в каждом языке программирования есть по крайней мере одно реальное магическое число.
Я утверждаю, что это волшебная палочка, чтобы управлять ими всеми практически в колчане каждого программиста волшебных палочек.
NULL неизбежно равно 0 (указатель) И большинство компиляторов позволяют это, если их проверка типов не является совершенно бешеной.
0-базовый индекс элементов массива, за исключением языков, которые настолько устарели, что базовый индекс ‘1’. Затем можно удобно кодировать для(i = 0; i
0-это конец многих языках программирования строки. Значение» stop here».
0 также встроен в инструкции X86 для «эффективного перемещения строк». Сохранить много микросекунд.
0 часто используется программистами, чтобы указать, что «ничего не случилось» в исполнении рутины. Это значение кода «не является исключением». Можно использовать его, чтобы указать на отсутствие исключений.
0 это количество ошибок в программе, которую мы стремимся достичь. 0 исключений неучтенных, 0 циклов unterminated, 0 путей рекурсии, которые фактически не могут быть приняты. 0-это асимптота, которую мы пытаемся достичь в программировании труда, подружки (или друга) «проблем», паршивых ресторанных впечатлений и общих особенностей своего автомобиля.
да, 0 действительно магическое число. Гораздо больше магии, чем любой другой ценности. Ничего. ГМ, идет. закрывать.
Ты не пройдёшь: магические числа для начинающих фронтендеров
Выводим Гэндальфа на чистую воду: что такое магические числа и почему верстальщику надо гнать их взашей из своего проекта.
Преподаватель в «Хекслете», автор Telegram-канала LayoutCoder.
Магическими называют такие числа в коде, смысл которых понятен только написавшему их программисту. Например, иногда в интернет-магазинах цену товара автоматически умножают на 1,2, вместо того чтобы ввести понятную переменную для НДС. И без комментариев такие коэффициенты понять очень сложно. Магические числа встречаются в любом языке программирования: JavaScript, Python, Ruby. Они есть даже в CSS.
Чтобы избавиться от магического числа в коде, достаточно ввести для индекса 1,2 специальную переменную VAT — тогда любому разработчику, который читает и дополняет ваш код, будет понятен «физический» смысл числа.
Веб-вёрстка близка к программированию, и проблема магических чисел здесь очень актуальна. Я преподаю и, комментируя код студентов, часто вижу, как отступы, длина, ширина блоков берутся практически с потолка. Постоянно попадаются записи вроде «width = 47%» — из них совершенно непонятно, почему взято именно 47%. Я-то понимаю: если на вёрстке пишут «47% от ширины», это чаще всего означает, что 3% ушло на отступы между блоками. Однако всё равно писать код нужно так, чтобы это было понятно без гаданий.
Магические числа определяют, насколько быстро верстальщик или разработчик, которые будут поддерживать код, разберутся, почему введены такие константы. В общем, проект нужно делать так, чтобы его логику понял даже бэкенд-разработчик, который практически не знает веб-вёрстку. Для этого во время написания кода надо постоянно задавать себе вопрос: «А поймёт ли код другой программист?»
В вёрстке проблема магических чисел решается просто — через переменные CSS или в препроцессорах. Например, она красиво решается в фреймворке Bootstrap — в нём есть отдельный файл _variables.scss, где прописаны все используемые переменные: какие сделаны отступы и почему, какие цвета применяются.
Как избавиться от магических чисел: три способа
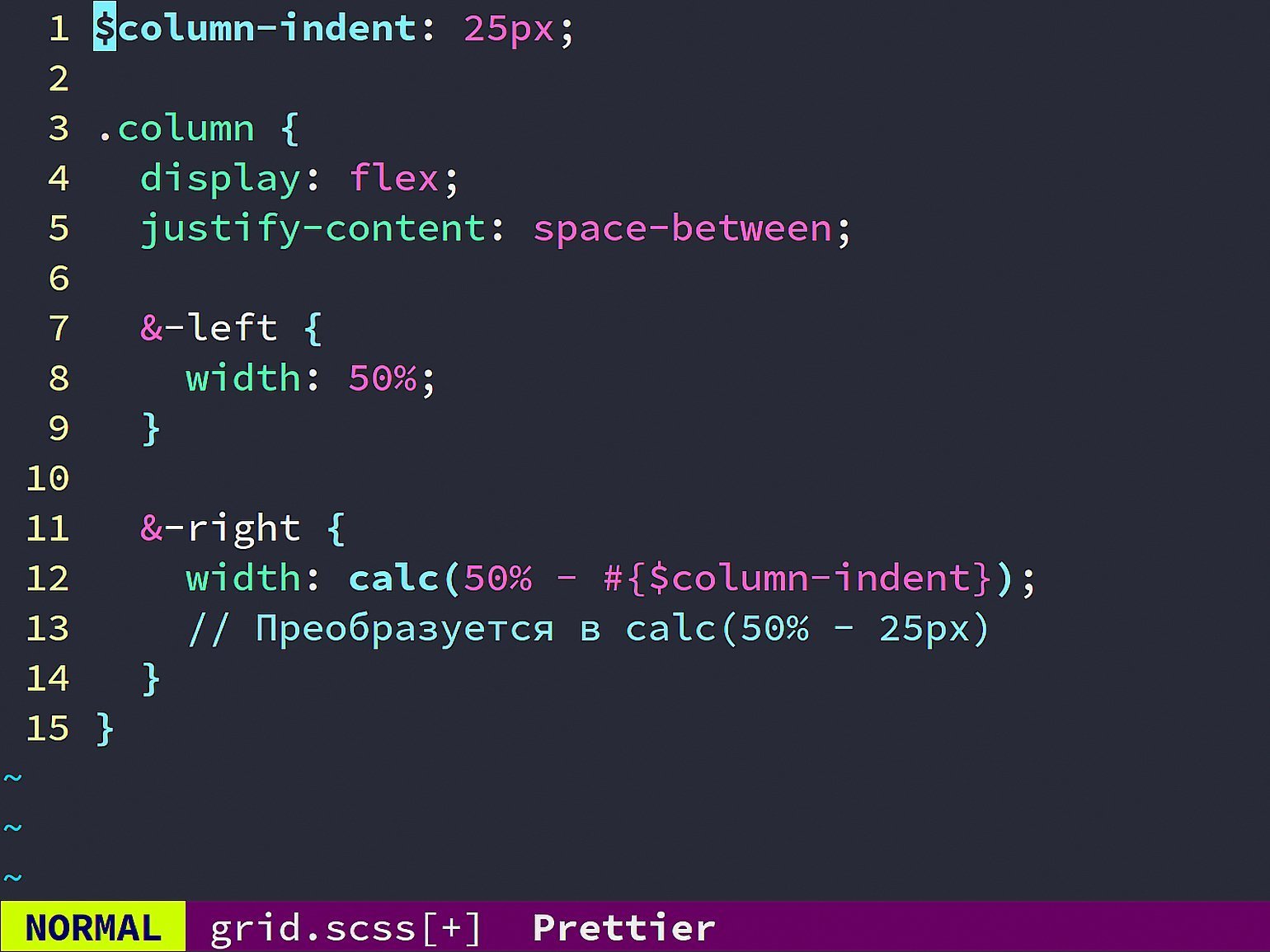
Разбивать проект на логические блоки и описывать его с точки зрения архитектуры: например, отступы между колонками, ширину бордеров и тому подобное выносить в переменные, чтобы назначение этих переменных было максимально очевидным. Например, если 3% уходит на отступы между блоками, стоит использовать встроенную в CSS функцию calc и передать в неё значение «50% минус размер отступа».
Не заигрываться с переменными — их не должно быть слишком много, иначе структура разрастётся и снова усложнится. Чаще всего переменные нужны на внутренних и внешних отступах и для цветов.
Стараться не подгонять макет с помощью мелких отступов. Например, если вы видите, что внешний отступ справа 43, а слева 32, то это тревожный звоночек — здесь что-то не так. Как правило, это попытка сделать что-то очень быстро и тут же выпустить в продакшн. Не надо так.
Магические числа — одна из самых распространённых проблем. Однако, чтобы её решить, не нужно алгоритмическое мышление или знание каких-то сложных систем и тайной науки. Если надо отрефакторить проект, однозначно придётся вычищать из него все магические числа. Правда, чаще всего они становятся едиными для всего проекта и используются повсюду, поэтому, чтобы их обнаружить, нужны опыт и насмотренность. А если удалось их найти — смело выводите в переменные и заменяйте.
Хотите научиться верстать сайты с нуля и делать уличную магию — записывайтесь на курс «Веб-вёрстка» в Skillbox.
обложка: olia danilevich / Ion Ceban / Matheus Bertelli / Skylar Kang / Pexels / Polina Vari для Skillbox
Антипаттерн №1 — Магическое число (Magic Number)
Из всего многообразия грехов разработки магическое число (magic number) — это, пожалуй, самый распространённый антипаттерн. Греховность его можно оценить как лёгкую, т.к., в целом, данный методологический изъян лёгок в обнаружении и устранении.
Магическое число — это оперирование явно указанными в коде коэффициентами (как правило целочисленными), значение и смысл которых знает только автор программы. Как правило, подобные волшебные числа встречаются в виде параметров, передаваемых при вызове методов\функций\процедур или же при присвоении каких-либо свойств\полей. Обязательно — без поясняющих комментариев. Изменение подобных коэффициентов порой несут абсолютно непредсказуемый характер и именно поэтому данный антипаттерн называется магическим числом 🙂 Возьмём канонический пример:
Пример с методом, который носит имя Draw на самом деле упрощён и даёт хоть какое-то поле для понимания кода: здесь однозначный нейминг и знакомые цифры 320×240 наталкивают на догадки. А вот что делать со следующим кодом:
Кроме очевидного затруднения чтения и понимания кода, магические числа служат источником инфраструктурных проблем и ошибок. При многократном использовании одного и того же числа во многих местах программы, когда в будущем появляется необходимость ввести изменения какого-либо коэффициента — нужно пройтись по всему исходному коду и везде заменить старое значение на новое. При этом массовая замена может разломать другие части программы, которые не требуется изменять. Особенно это касается, когда искомая фраза может быть вхождением в другие магические числа, которые менять не нужно. Одна подобная замена по всему проекту итого отнимет несколько часов на дебаг.
Как исправить? Вводить однозначные константы или же списки Enum (с ними нужно быть тоже очень осторожными, т.к. есть некоторые ньюансы при использовании в больших командах, при поддержании обратной связи и т.д.):
Или же пример с списком Enum :
По-меньше вам магических чисел в коде, братцы.
Магические константы в алгоритмах
Введение
В настоящее время широко известны такие принципы написания программного кода (coding standards), которые позволяют облегчить его поддержку и развитие. Эти принципы используются многими софтверными компаниями, а средства разработки и статического анализа кода предлагают для этого разнообразную автоматизацию. В то же время инженерные задачи в программировании явно требуют расширения понятия «хороший код». Мы попробуем выйти на обсуждение «хорошего» инженерного кода через, казалось бы, весьма частный пример — через практику использования в алгоритмах константных параметров.
Сразу хочется отметить, что эта статья ставит перед собой задачу повышения самоконтроля разработчика, особенно начинающего свою карьеру. Все приведенные далее примеры нужно рассматривать как модельные ситуации, вне привязки к какой-то конкретной вычислительной задаче или какому-то конкретному алгоритму. Можно сказать, что наша цель — сформулировать некоторые паттерны качественного инженерного/алгоритмического программирования.
Давайте подумаем, режет ли нам глаз такой код:
Лично мне режет очень сильно. Во-первых, совершенно непонятно, что такое 150.7?
Вполне возможно, что 150.7 — это сопротивление точного резистора, которое варьируется от одного экземпляра устройства к другому, и на самом деле должно быть считано из калибровочного файла. Что же такое 0.002? Похоже, что это некоторый экспериментальный порог, который может быть уточнен впоследствии, хотя об этом нет никакого специального комментария.
Первая кровь
Представим себе junior-программиста Алешу, которому предложили задачу по автоматизации контроля качества заклепок для космических кораблей компании Inhabited Galactic. По конвейеру поступают эти заклепки и их фотографирует цифровая камера. Алеше необходимо написать код, который анализирует фотографии этих заклепок и принимает решение о соответствии или несоответствии формы заклепки ее нормативу.
Предположим, что к удовольствию своих начальников Алеша быстро реализовал некоторый алгоритм оценки заклепок. Этот алгоритм отлично разделял изображения плохих и хороших заклепок из тестового набора, задача была решена и Алешу переключили на другой проект.
Затем произошло следующее. Заклепок пошло несколько больше, скорость конвейера возросла и инженер Боря немного укоротил выдержку камеры.
При этом поступающие с камеры изображения стали несколько темнее, хотя заклепки все еще были хорошо видны. В то же время Алешин алгоритм начал иногда ошибочно браковать качественные заклепки. Что же произошло?
Пусть это входное монохромное изображение размера
с координатами
и
. Алеша заметил, что пискели заклепки
во всех тренировочных изображениях можно было найти пороговой фильтрацией:
При этом качественную заклепку можно было найти по площади:
Итого, Алеша ввел 4 эмпирических константы ,
,
и
, по крайней мере одна из которых (
) потеряла актуальность после перенастройки камеры.
Немного набравшись опыта, Алеша мог бы сделать следующее: перенести значения необходимых констант в конфигурационный файл и дополнить проектную документацию методом их практического вычисления. Это было бы лучше, чем просто спрятать эти значения внутри своего кода, но возложило бы на Алешиных коллег дополнительную задачу по ручной настройке его алгоритма. Конечно, такое решение трудно назвать удовлетворительным, хотя в особенно трудных ситуациях и оно имеет право на существование.
Какое решение было бы более разумным? Параметры полосовых фильтров для яркости и площади можно было перевести в относительные величины к средней яркости и площади изображения. Например, можно было бы заменить на
, где
— тоже эмпирическое, но уже более инвариантное значение.
Давайте попробуем предположить, что произошло дальше на заводе космических кораблей.
Так как качество отбраковки заклепок было недостаточным, то главный технолог Виталий, далекий от тонкостей программирования, решил срочно поставить на оценочный стенд более дорогую камеру с высокой чувствительностью и вдвое большим разрешением. Закономерный результат такой командной работы — 100%-ая отбраковка, так как все заклепки стали вдвое больше по числу пикселей и ни одна из них не прошла полосовой фильтр. Возможно, что спасло бы грамотное управление проектом, но сейчас мы не об этом.
Нормализация входных данных
Многих проблем с подбором констант можно избежать приводя входные данные к единообразному виду. Изображения — к одной форме гистограммы, 3D модели — к одному разрешению, etc. Зачастую против нормализации выдвигают такой аргумент, что она приводит к потере части исходной информации. Это действительно так, но упрощение дальнейшей работы с параметрами алгоритмов зачастую перевешивают этот минус.
Сама постановка задачи о максимальной нормализации входных данных позволяет разработчику подумать о том, что будет, если изображения придут с поворотом на 90 градусов? А если размеры придут в дюймах? А если кто-то передаст на вход 3D-модель высокого разрешения, которая передает тонкую фактуру материала?
Отличный пример, когда нормализацию, тем не менее, делать не нужно — поиск засвеченных пикселей (бликов) на фотографиях. Пиксели с максимальной яркостью RGB(255, 255, 255) могут образовывать тонкие полоски, которые немного смазываются во время масштабирования картинки. При этом этого яркость засвеченных пискелей усредняется с соседними пикселями и их становится почти невозможно отличить от просто ярких точек изображения. Соответственно, не удастся точно выделить и вырезать блики из изображения.
Калибровочные константы
При обработке достаточно низкоуровневых данных возникает классическая задача калибровки. Это может быть и преобразование напряжения на каком-нибудь терморезисторе в температуру, и преобразование отклика радара в координаты наблюдаемого объекта. Все эти преобразования так или иначе определяются набором постоянных параметров, а процедура определения этих параметров и называется калибровкой.
Калибровочные параметры как правило поступают из внешних источников. Страшный грех — захардкодить эти параметры. Если такой код сразу не отсеять на code review, то он сможет долго портить поведение программного продукта в целом, оставаясь при этом вне подозрений. Система просто будет работать не совсем точно, но едва ли где-то выскочит сообщение об ошибке.
Для полноты картины, однако, необходимо отметить, что в некоторых задачах возможна автокалибровка, когда внутренние зависимости наблюдаемых величин позволяют вычислить также и калибровочные параметры. Смотрите, например, последние главы Multiple View Geometry или работы по Uncalibrated Structure from Motion, где калибровочные параметры камер определяются из набора перекрывающихся снимков с разными ракурсами.
Общие замечания
Давайте константам осмысленные имена и комментируйте их значения. Помните, что это очень хрупкая часть кода, которая не защищена типизацией языка или мудростью компилятора.
Группируйте параметры алгоритмов в структуры. Это обычно улучшает читаемость кода и позволяет не прозевать какой-нибудь важный параметр во время отладки.
Если вы знаете, что один какой-то параметр выражается через другие, обязательно отразите эту связь в коде. В противном случае кто-нибудь с самыми лучшими намерениями поменяет ваши неоптимальные, но консистентные параметры на неконсистентные. Например, вы ищете на изображении кружочки радиусом = 10 и площадью
= 314. Это плохо, так как на самом деле у вас один параметр — радиус
= 10, а
. Код с двумя параметрами может быть легко сломан программистом, забывшим школьную математику, а код с одним параметром выглядит гораздо надежнее.
Бывает так, что в алгоритм входит какая-то неэмпирическая константа. Например, нужно оценить хвост какого-нибудь распределения. Точность такой оценки определяется в большей степени математической подготовкой автора алгоритма.
Константы-оценки иногда можно улучшать, но такое улучшение обычно является изолированной задачей. Важно прокомментировать этот факт для других разработчиков.
Урок №36. Литералы и магические числа
Обновл. 11 Сен 2021 |
В языке C++ есть два вида констант: литеральные и символьные. На этом уроке мы рассмотрим литеральные константы.
Литеральные константы
Литеральные константы (или просто «литералы») — это значения, которые вставляются непосредственно в код. Поскольку они являются константами, то их значения изменить нельзя. Например:
С литералами типов bool и int всё понятно, а вот для литералов типа с плавающей точкой есть два способа определения:
Во втором способе определения, число после экспонента может быть и отрицательным:
Числовые литералы могут иметь суффиксы, которые определяют их типы. Эти суффиксы не являются обязательными, так как компилятор понимает из контекста, константу какого типа данных вы хотите использовать.
| Тип данных | Суффикс | Значение |
| int | u или U | unsigned int |
| int | l или L | long |
| int | ul, uL, Ul, UL, lu, lU, Lu или LU | unsigned long |
| int | ll или LL | long long |
| int | ull, uLL, Ull, ULL, llu, llU, LLu или LLU | unsigned long long |
| double | f или F | float |
| double | l или L | long double |
Суффиксы есть даже для целочисленных типов (но они почти не используются):
По умолчанию литеральные константы типа с плавающей точкой являются типа double. Для конвертации литеральных констант в тип float можно использовать суффикс f или F :
Язык C++ также поддерживает литералы типов string и char:
Литералы хорошо использовать в коде до тех пор, пока их значения понятны и однозначны. Это выполнение операций присваивания, математических операций или вывода текста в консоль.
Литералы в восьмеричной и шестнадцатеричной системах счисления
В повседневной жизни мы используем десятичную систему счисления, которая состоит из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. По умолчанию язык C++ использует десятичную систему счисления для чисел в программах:
В двоичной (бинарной) системе счисления всего 2 цифры: 0 и 1. Значения: 0, 1, 10, 11, 100, 101, 110, 111 и т.д.
Есть еще две другие системы счисления: восьмеричная и шестнадцатеричная.
Восьмеричная система счисления состоит из 8 цифр: 0, 1, 2, 3, 4, 5, 6 и 7. Значения: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12 и т.д.
Примечание: В восьмеричной системе счисления нет цифр 8 и 9, так что сразу перескакиваем от 7 к 10.
| Десятичная система счисления | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Восьмеричная система счисления | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 |
Для использования литерала из восьмеричной системы счисления, используйте префикс 0 (ноль):
Результат выполнения программы:
Почему 10 вместо 12? Потому что std::cout выводит числа в десятичной системе счисления, а 12 в восьмеричной системе = 10 в десятичной.
Восьмеричная система счисления используется крайне редко.
Шестнадцатеричная система счисления состоит из 16 символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F.
| Десятичная система | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| Шестнадцатеричная система | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 |
Для использования литерала из шестнадцатеричной системы счисления, используйте префикс 0x :
Результат выполнения программы:
Поскольку в этой системе 16 символов, то одна шестнадцатеричная цифра занимает 4 бита. Следовательно, две шестнадцатеричные цифры занимают 1 байт.
До C++14 использовать литерал из двоичной системы счисления было невозможно. Тем не менее, шестнадцатеричная система счисления может нам в этом помочь:
Бинарные литералы и разделитель цифр в C++14
В C++14 мы можем использовать бинарные (двоичные) литералы, добавляя префикс 0b :
Поскольку длинные литералы читать трудно, то в C++14 добавили возможность использовать одинарную кавычку ‘ в качестве разделителя цифр:
Если ваш компилятор не поддерживает C++14, то использовать бинарные литералы и разделитель цифр вы не сможете — компилятор выдаст ошибку.
Магические числа. Что с ними не так?
Рассмотрим следующий фрагмент кода:
В вышеприведенном примере число 30 является магическим числом. Магическое число — это хорошо закодированный литерал (обычно, число) в строке кода, который не имеет никакого контекста. Что это за 30, что оно означает/обозначает? Хотя из вышеприведенного примера можно догадаться, что число 30 обозначает максимальное количество учеников, находящихся в одном кабинете — в большинстве случаев, это не будет столь очевидным и понятным. В более сложных программах контекст подобных чисел разгадать намного сложнее (если только не будет соответствующих комментариев).
Использование магических чисел является плохой практикой, так как в дополнение к тому, что они не предоставляют никакого контекста (для чего и почему используются), они также могут создавать проблемы, если их значения необходимо будет изменить. Предположим, что школа закупила новые парты. Эта покупка, соответственно, увеличила максимально возможное количество учеников, находящихся в одном кабинете, с 30 до 36 — это нужно будет продумать и отобразить в нашей программе.
Рассмотрим следующий фрагмент кода:
Чтобы обновить число учеников в кабинете, нам нужно изменить значение константы с 30 на 36. Но что делать с вызовом функции setMax(30)? Аргумент 30 и константа 30 в коде, приведенном выше, являются одним и тем же, верно? Если да, то нам нужно будет обновить это значение. Если нет, то нам не следует вообще трогать этот вызов функции. Если же проводить автоматический глобальный поиск и замену числа 30, то можно ненароком изменить и аргумент функции setMax(), в то время, когда его вообще не следовало бы трогать. Поэтому вам придется просмотреть весь код «вручную», в поисках числа 30, а затем в каждом конкретном случае определить — изменить ли 30 на 36 или нет. Это может занять очень много времени, кроме того, вероятность возникновения новых ошибок повышается в разы.
К счастью, есть лучший вариант — использовать символьные константы. О них мы поговорим на следующем уроке.
Правило: Старайтесь свести к минимуму использование магических чисел в ваших программах.
Поделиться в социальных сетях:
Урок №35. Символьный тип данных char
Комментариев: 25
Подскажите пожалуйста что тогда не является литералом? Раз буквы, цифры и символы это литералы, тогда нелитерал этот только переменная
литерал по простому это значение переменной оно может быть любого типа кроме void
Ну 30 конечно никто не пишет. а пишут или именованную константу или макрос. Насчёт литералов. Да удобно. Но можно использовать и свои литералы. Последние версии С++ это позволяют. Хотя код становится малопонятным если вы туда понапихаете кучу своих литералов… В С кстати бинарный литерал тоже есть. Это не прерогатива С++. Насчёт групп ну мне не нравится. Я не люблю группированные числа… Особенно в виде строк, а не констатнт. С ними столько возни… Но это моё личное мнение.
Я всегда сравниваю С/С++ с фортраном. Как там? Там вообще задаётся размер типа… А функции универсальны… Если ваш комп не поддерживает этот размер вылетит ошибка… Я не пропагандирую фортран. Но концепция типов в С/С++ мягко говоря ущербна. Ибо там изначально заложили в названия типов их размен. В фортране такое тоже было. Но сейчас нет. И правильно. Я молу легко работать с любыми типами и они все работают. И там не надо выдумывать дурацкие названия. Просто пишешь типа real(16) и всё у вас тип _float128. Или integer(16) и вуаля у вас тип __int128. Никаких проблем. Да, фотран это вам не Си… Хотите его преобразовать в строку? Да пожалуйста! Там нет многочисленных функций преобразований как в Си. Всего 2 write и read, но онир делают всё и гораздо лучше где либо. И в любой системе счисления. Даже двоичной. Конечно есть библиотека gmp. Там можно использовать числа любого размера. главное чтобы в память поместилось… Но то библиотека. А это аппаратная поддержка! А функция скажем sin там всего одна, но на все случаи жизни. Да фортран не поддерживает беззнаковые числа. Ну и ладно… Но слышал, что компилятор ifort их поддерживает. но он платный… Поэтому если на С/С++ вам понадобятся эти типы данных, то ни одна библиотека не будет с ними работать. Но сами типы там есть… вам придётся все эти функции писать самим. Особенно если вам понадобится двоичный формат… Или подключите модуль на фортране, там это уже есть. В Qt кстати поддержка функций есть… Но нет преобразований в строки. Эта среда более продвинута, чем С/С++. Хотя это только если вы используете это Qt.
Немного мудрёные формулировки с магическими числами. Константы предполагаются как неизменяемые. Если есть вероятность, что константу придётся изменить, надо изначально создавать переменную, не придумывая названий для «изменяемой константы». Хотя можно написать десять программ для десяти разных чисел парт в классе, но программистами всё равно станут только адекватные люди.
Понятие переменной подразумевает изменение в течение одного запуска программы. Тогда как значение константы остается неизменным в течение одного запуска, но может быть изменено между запусками.
Пояснение для тех, кто, как и я, сначала не понял, как связаны следующие присваивания с комментариями:
Например, мы хотим понять, почему 0x80 — это 1000 0000.
80 в шестнадцатеричной системе переведём в привычную десятеричную, для этого каждая цифра справа налево умножается на степени 16, начиная от 0: 0х80=0*1+8*16=0+128=128
128 переводим в двоичную систему, 128 — это 2 в 7 степени, значит двоичная запись будет 1000 0000 (тут тоже степени двойки справа налево, начиная с 0). Подробные пояснения по переводу из одной системы в другую есть в 44 уроке.
Скорей всего, всё можно понять и проще, осознав чудо превращения сразу из 16-ричной системы в двоичную. Кто осознал, делитесь.
Хорошая демонстрация и объяснение, как быстро переводить числа из двоичной системы в шестнадцатеричную, есть здесь.
Есть гораздо более удобный способ конвертации чисел в двоичную систему и из неё. Достаточно выучить таблицу тетрад (а в ней же и триад(а в ней же диад)) чтобы на ходу переводить числа из четверичной/восьмеричной/шестнадцатеричной системы счисления.
Жаль, что пока не знаю как всё быстро и на ходу в десятеричную систему переводить, но пока поделюсь тем, что есть.
(exe.exe.exe, попыталась это всё расписать, но здесь нужно наглядное представление)
Пожалуй, лучшее объяснение есть у информатика бу. А вот и ссылка: https://www.youtube.com/watch?v=npB8lF-V4mc&list=PLgvtHXe0kJXaNH57H5yolkewq-p5hfpDR
Не надо переводить в десятичную и обратно. Всё просто, никакой магии:
Для кодирования 0,1 нужен1 бит.
То есть 4 бита можно выразить либо 16-ю двоичными комбинациями:
0000
0001
0010
.
1111
В книге Чарльза Петцольда «КОД. Тайный язык информатики» есть глава, где системы счисления ассоцируются с количеством пальцев на руках и остальных существ планеты. У человека 10 пальцев и поэтому он привык считать в десятичной системе счисления, то есть если вести счет 0,1,2,3,4,5,6,7,8,9 после девяти идет 11-ая цифра (0 это первая) и добавляется новый разряд числа — единица и счет продолжается с ним 10,11,12,13… и так далее. Но если бы мы были дельфинами, то счет бы был в двоичной системе, потому что «пальцев»(плавников) то два, то есть мы могли бы считать только до двух, а после добавлялся бы новый разряд единицы: то есть после счета чисел 0, 1 добавляется новый разряд числа и получаем 10, 11 дальше — третий разряд и получаем сразу 100, 101, 110, 111 что равносильно в нашей десятичной системе числам 5, 6, 7, 8.
Каждый разряд в двоичной системе можно сравнить с битом, где 1 бит может хранить два возможных значения это 0 и 1. 2 бит — 4 значения это 00, 01, 10 11. 3 бит — 8 значений это 000, 001, 010, 011, 100, 101, 110, 111. С каждым добавлением нового разряда количество возможных значений удваивается от крайнего значения предыдущего(младшего) разряда. 1 бит- 2 значения, 2 бит = (2)*2 значения, 3 бит = (2*2)*2 значений, 4 бит = (2*2*2)*2 возможных значений отсюда и формула [количества возможных значений] = 2^(количество бит(разрядов двоичного числа)).
Дальше шестнадцатеричная система счисления будет обозначаться как hex (сокр. от hexadecimal)
Одно шестнадцатеричное число занимает 4 бит, потому что для представления 16 значений 3 битов будет недостаточно, 2^3 = 8, 2^4 = 16. Соответственно первое число в hex (0) в двоичном представлении будет 0000, второе число (1) — 0001, восьмое число (7) — 0111, девятое (8) — 1000, десятое и одиннадцатое (9) и (A) — 1001 и 1010. В программе выше переменной присваивается литерал в виде двух чисел hex, каждое из которых занимает по 4 бит. Вот и каждому hex числу соответствует свой бинарный код.
Прошу строго не судить за ответ, я еще только начинаю осваивать базы, что то дается хорошо, что то не очень. Поправьте если нужно.
Мой препод по программированию приводил хороший пример. Программирование как занятия музыкой. Чтобы развиваться, нужно заниматься постоянно, часами и сутками. А вот мой пример. Чтобы начать играть на инструменте, надо выучить ноты. Базовый курс информатики помогает с пониманием систем счисления и прочих важных мелочей.
Спасибо, отличный перевод, все очень понятно.
Понятно почему вы не перевели слово statement (заявление? утверждение? высказывание? изложение?), но в этой статье (простите за придирку)
> число avogadro
число Авогадро оставили непереведенным, несмотря на то, что оно вполне себе имеет общепризнанный перевод.
Чтобы можно было применять цифровые разделители, т.е. записывать литералы в виде: