Монады за 15 минут
Вступление
На конференции YOW! 2013 один из разработчиков языка Haskell, проф. Филип Вадлер, показал, как монады позволяют чистым функциональным языкам осуществлять императивные по сути операции, такие, как ввод-вывод и обработку исключений. Неудивительно, что интерес аудитории к этой теме породил взрывной рост публикаций о монадах в Интернет. К сожалению, бо́льшая часть этих публикаций использует примеры, написанные на функциональных языках, подразумевая, что о монадах хотят узнать новички в функциональном программировании. Но монады не специфичны для Haskell или функциональных языков, и вполне могут быть проиллюстрированы примерами на императивных языках программирования. Это и является целью данного руководства.
Чем это руководство отличается от остальных? Мы попытаемся не более чем за 15 минут «открыть» монады, используя лишь интуицию и несколько элементарных примеров кода на Python. Мы поэтому не станем теоретизировать и углубляться в философию, рассуждая о буррито, космических скафандрах, письменных столах и эндофункторах.
Мотивационные примеры
Мы рассмотрим три проблемы, относящиеся к композиции функций. Мы решим их двумя способами: обычным императивным и при помощи монад. Затем мы сравним разные подходы.
1. Логгирование
Можно добиться нужного нам результата следующим способом:
Это решение неидеально, так как состоит из большого количества однообразного связующего кода. Если мы захотим добавить к нашей цепочке новую функцию, мы вынуждены будем повторить этот связующий код. Кроме того, манипуляции с переменными res и log ухудшают читаемость кода, мешая следить за основной логикой программы.
Теперь мы можем решить проблему следующим образом:
И никаких других изменений нам делать не понадобится.
2. Список промежуточных значений
Этот пример мы также начнём с простых унарных функций.
В отличие от предыдущего примера, наши функции компонуемы, то есть типы их входных параметров совпадают с типом результата. Поэтому простая цепочка f3(f2(f1(x))) вернёт нам конечный результат. Но в таком случае мы потеряем промежуточные значения.
Решим задачу «в лоб»:
Поэтому добавим две дополнительные функции, как и в предыдущем примере:
Теперь мы перепишем программу в виде цепочки вызовов:
3. Пустые значения
Попробуем привести более интересный пример, на этот раз с классами и объектами. Допустим, у нас есть класс Employee с двумя методами:
Каждый объект класса Employee имеет руководителя (другой объект класса Employee ) и зарплату, доступ к которым осуществляется через соответствующие методы. Оба метода могут также возвращать None (работник не имеет руководителя, зарплата неизвестна).
В идеале нам нужно написать что-то вроде
Очевидный способ учесть эту ситуацию может выглядеть так:
И теперь мы можем скомпоновать всё решение в одну строку.
Как вы, наверное, уже заметили, в этом случае нам не обязательно было писать функцию unit : она просто возвращает входной параметр. Но мы оставим её, чтобы нам легче было потом обобщить наш опыт.
Выводы
Зачастую этот подход неприменим. Типы входных значений и результатов функций могут различаться, как в первом примере. Либо же функции могут быть компонуемы, но мы хотим вставить дополнительную логику между вызовами, как в примерах 2 и 3 мы вставляли аггрегацию промежуточных значений и проверку на пустое значение соответственно.
1. Императивное решение
Во всех примерах мы вначале использовали самый прямолинейный подход, который можно отобразить следующей диаграммой:
2. Монады
Процесс вычисления можно представить диаграммой:
Наконец, рассмотрим, как можно улучшить код, написанный с использованием монад. Очевидно, повторяющиеся вызовы bind выглядят неэлегантно. Чтобы избежать этого, определим ещё одну внешнюю функцию:
мы можем использовать следующее сокращение:
Заключение
Монады − это простой и мощный шаблон проектирования, используемый для композиции функций. В декларативных языках программирования он помогает реализовать такие императивные механизмы, как логгирование или ввод/вывод. В императивных языках
он помогает обобщить и сократить код, связывающий серию вызовов однотипных функций.
Эта статья даёт только поверхностное, интуитивное понимание монад. Вы можете узнать больше, обратившись к следующим источникам:
Записки программиста
Собираемся с духом и перестаем бояться монад
Что такое монада?
В Haskell монада — это совершенно обычный класс типов:
Функции (>>=), (>>), return и fail
Давайте временно забудем о монадах вообще и подумаем об одной конкретной, всем хорошо знакомой, монаде IO. Если заменить в перечисленных ранее функциях «m» на «IO», получим:
Вспомним тип функции putStrLn:
Очень, очень хорошо! А что, если у нас есть чистая функция, возвращающая строку, и мы хотим вывести ее при помощи putStrLn? Мы не можем просто поместить функцию в цепочку, потому что после применения к своим аргументам она будет иметь тип String, а нам нужен IO String. Вот для этого и нужна функция return, которая «оборачивает» произвольный тип в монаду:
Наконец, функция fail нужна для обработки исключительных ситуаций. В контексте монады IO она бросает исключение IOError. Хотя, в зависимости от конкретной монады, она может делать и что-то более осмысленное.
do-нотация
Все это замечательно, но при работе с монадой IO мы же просто пишем:
Никаких стрелочек! Как же так? В действительности, приведенный выше код полностью аналогичен следующему:
Другими словами, do-нотация — это просто синтаксический сахар над стрелочками. Можно спокойно писать на Haskell без нее, просто код будет чуть менее понятен и придется вводить чуть больше символов.
Кстати, при работе в ghci мы на самом деле находимся внутри монады и используем do-нотацию.
Монадные законы
Когда вы работаете с монадами, предполагается, что выполняются следующие правила:
Компилятор не может проверить выполнение этих законов на этапе компиляции, поэтому ответственность за их соблюдение при объявлении новых монад ложиться на программиста. Если внимательно присмотреться, первые два правила напоминают свойство существования нейтрального элемента, а последнее — это что-то вроде ассоциативности. Давайте проверим на примерах, что эти правила выполняются для монады IO.
Разумеется, строго доказать, что все три закона всегда выполняются для некоторой монады, намного сложнее. Впрочем, как я понимаю, обычно в этом вопросе программисты полагаются либо на интуицию, либо на тесты.
Монада Maybe
В заметке Пишем простой RESTful сервис с использованием Scotty мы видели такую вот странную функцию:
Давайте разберемся, как это работает. Экземпляр класса Monad для типа Maybe определен следующим образом:
instance Monad Maybe where
( Just x ) >>= k = k x
Nothing >>= _ = Nothing
( Just _ ) >> k = k
Nothing >> _ = Nothing
return = Just
fail _ = Nothing
Если бы Maybe не был монадой, а нам нужно было бы извлечь из Map’а десяток значений, пришлось бы написать десяток вложенных case of. Кроме того, что монады в данном случае позволяют писать меньше кипятильно-тарелочного кода, также мы фактически получаем что-то вроде механизма исключений для чистых функций.
Благодаря do-нотации мы можем записать это выражение еще проще. А при помощи аппликативных функторов можно записать его вообще в одну строку. Однако об аппликативных функторах речь пойдет как-нибудь в другой раз.
Монада Either
В модуле Control.Monad.Error объявлен экземпляр класса Monad для типа Either:
Здесь все работает аналогично Maybe, только вместо того, чтобы в случае неудачи просто возвращать Nothing, мы можем как-то уточнить причину ошибки.
Монада State
Монада State бывает полезна, когда имеется некоторое состояние, которое мы постоянно изменяем. Например, если у нас есть Map, в который мы хотим поместить десять значений, возвращаемых разными функциями, нам придется ввести множество переменных m0, m1, m2, … m9. Благодаря монаде State мы можем создать изменяемое состояние, не потеряв при этом чистоты функций, и избежать тем самым описанной проблемы.
Работает это как-то так:
Здесь Int — это наше состояние, а String — как бы значение, возвращаемое функцией. Получить текущее состояние можно с помощью функции get, сохранить — при помощи put, а изменить — при помощи modify. Для выполнения функции и получения возвращаемого ею значения используйте evalState. Если же вы хотите получить конечное состояние, воспользуйтесь execState. Если вам нужно как возвращаемое значение, так и конечное состояние, скажите runState.
В do-нотации монада State, конечно, выглядит намного красивее.
Монада Reader
Это своего рода State, доступный только на чтение. Монада Reader удобна в случае, когда у нас есть множество функций, работающих в некотором неизменяемом окружении. Вместо того, чтобы передавать между этими функциями одни и те же параметры, мы можем завернуть их в монаду Reader.
С помощью функции local мы можем создать скоп с измененным окружением. Это намного удобнее, чем читать окружение и создавать на его основе новое. Функция ask возвращает текущее окружение. Функция asks применяет заданную функцию к текущему окружению и возвращает результат. Ее удобно использовать в сочетании с селекторами.
По понятным причинам функций execReader и evalReader не предусмотрено.
Монада Writer
Если Reader — это State, из которого можно только читать, то Writer — это State, в который можно только писать. Монада Writer часто применяется для логирования и трассировки без потери чистоты функций.
Функция tell производит запись в лог. Интересно, что лог при этом должен быть моноидом. В рамках данного поста будет достаточно сказать, что списки являются моноидами. Функция censor применяется для модификации записей в логе. Функция listen превращает Writer, который возвращает a и пишет w, во Writer, который возвращает (a, w) и пишет w. Функция listens позволяет делать с логом что угодно. Мы можем отфильтровать записи в нем, добавить новые, привести их к другому типу или сделать все это одновременно.
Монада [] (список)
Список тоже являются монадой. Вот классический пример:
— почему при игре в кости выгодно ставить на семь
Вызываем функцию main:
Можно сказать, что это другой способ записи генераторов списков.
Некоторые функции для работы с монадами
В модуле Control.Monad вы найдете множество обобщенных функций для работы с монадами. О назначении большинства из них несложно догадаться по названию и типу, поэтому я просто приведу список:
Поэкспериментируйте с ними на досуге в ghci с конкретными монадами, например, IO, Maybe и [], чтобы разобраться, как эти функции работают. Если хотите, можете считать это своим домашним заданием.
Заключение
Помимо перечисленных в данной заметке монад есть и другие. Например, уже знакомая нам монада STM, а также Indentity, монада цитирования Q, Error, ST, Cont, Eval, Par, ActionM и многие другие. В языке Scala много, так сказать, завуалированных монад, среди которых особый интерес представляет Future. Еще в Haskell есть моноиды, MonadPlus, функторы, аппликативные функторы, monad trasformer’ы и другие интересные вещи. Но эти вопросы выходят за рамки поста.
В качестве источников дополнительной информации я бы советовал:
Как видите, все прекрасно работает безо всяких там погружений в теории категорий и прочие матаны. Поначалу монады выглядят немного пугающе, потому что в мейнстримовых языках ничего подобного нет. Но если вы обладаете достаточным терпением, а также достаточной незамутненностью сознания, то скоро у вас начнет вызывать удивление, как вообще можно писать что-то серьезное без использования монад.
Дополнение: Вот отличный пример для медитации:
Попробуйте посмотреть на типы в REPL и понять, как это работает.
Монады с точки зрения программистов (и немного теории категорий)
Введение
Как узнать, что человек понял, что такое монады? Он сам вам об этом расскажет в первые 5 минут общения и обязательно попробует объяснить. А ещё напишет об этом текст и по возможности где-нибудь его опубликует, чтобы все остальные тоже поняли, что такое монады.
Среди функциональных программистов, особенно на Haskell, монады стали чем-то вроде локального мема. Их часто пытаются объяснить, отталкиваясь от частных случаев и сразу приводя примеры использования. Из-за этого слушатель может не уловить основную суть понятия, а монады так и останутся чёрной магией, ну или просто средством костылизации побочных эффектов в чисто функциональных языках.
Я сначала расскажу про базовые понятия теории категорий, а затем мы с практической точки зрения подойдём к определению монады и увидим, что на самом деле очень многие программисты пользуются этой мощной абстракцией в одном из её проявлений.
Моё изложение во многом основывается на книге Бартоша Милевски «Теория категорий для программистов», которая создавалась как серия блогпостов, доступна в PDF, а недавно вышла в бумаге.
Примеры приводятся на Haskell, предполагается, что читатель знаком с синтаксисом и основными понятиями языка. В упомянутой книге есть примеры и на С++, можете сравнить чистоту и понятность кода.
Категории
Определение
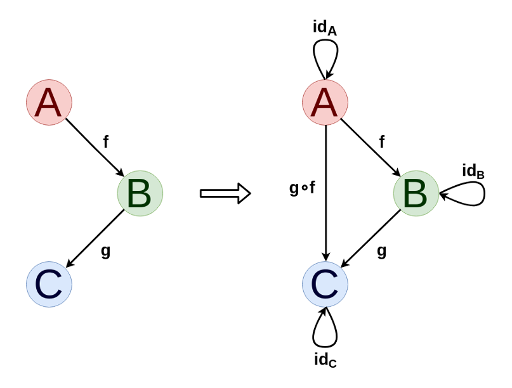
Категории сами по себе — очень простые конструкции. Категория — это набор объектов и морфизмов между ними. Морфизмы можно рассматривать как однонаправленные стрелки, соединяющие объекты. В общем случае про сущность самих объектов ничего не известно. Теория категорий работает не с объектами, а с морфизмами, точнее — с их композицией.
Используется следующая нотация:
В определении категории на морфизмы накладываются дополнительные ограничения:
Существуют два важных свойства, которым должна удовлетворять любая категория (аксиомы теории категорий):
Категории очень легко и естественно визуализируются как ориентированные графы. В принципе, любой ориентированный граф можно достроить до категории, добавив композиции морфизмов и тождественные морфизмы, если необходимо.
Объекты и морфизмы не обязательно образуют множества (в классическом смысле из теории множеств), поэтому в общем случае используется словосочетание «класс объектов». Категории, в которых классы объектов и морфизмов всё-таки являются множествами, называются малыми категориями. Далее мы будем работать только с ними.
Типы и функции
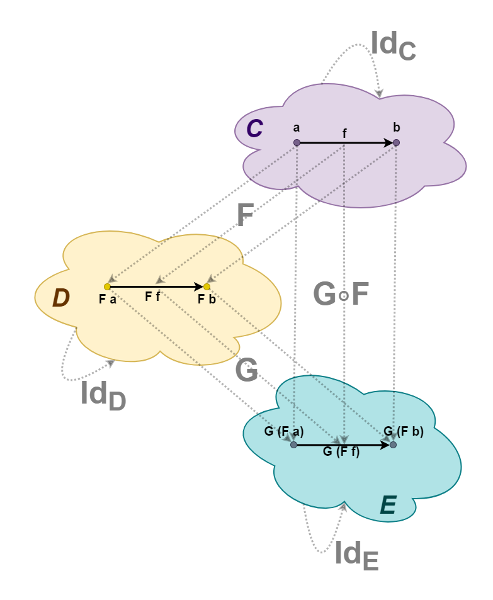
Композиция морфизмов — это композиция функций, причём синтаксис этой операции на Haskell почти идентичен математической нотации:
Рассмотрим несколько примеров типов с точки зрения теории категорий.
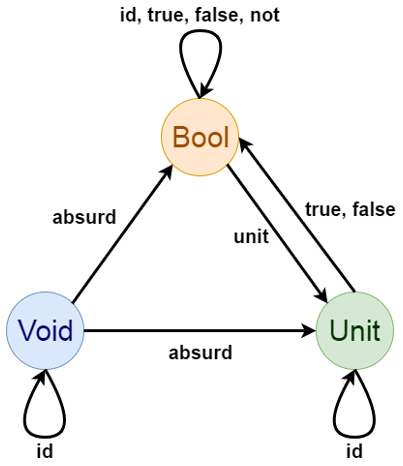
Множество из двух элементов — логический тип Bool :
Добавив тождественные морфизмы, получим следующую категорию:
В дальнейшем изложении будем использовать Haskell-подобную нотацию сигнатуры типов для обозначения морфизмов.
Функторы
Кроме того, должны выполняться «законы сохранения» композиции и тождественного морфизма:
Таким образом, функтор не «ломает» структуру категории: то, что было связано морфизмом в исходной категории, будет связано и в результирующей. Это верно и для крайних случаев, например, когда результирующая категория состоит из одного объекта. Тогда все морфизмы исходной категории отобразятся в тождественный морфизм для этого объекта, но упомянутые выше законы нарушены не будут.
Посмотрим на эту картинку сильно издалека, так, чтобы сами категории превратились в точки-объекты, а функторы — в стрелки между ними (морфизмы). Получим категорию малых категорий, которая называется Cat (название периодически порождает сложные мемы с кошками).
Вернёмся к категории типов языка Haskell и будем работать с эндофункторами в этой категории. Они преобразуют типы в другие типы и, кроме того, каким-то образом преобразуют функции, работающие с этими типами.
Конструктор типа Maybe является примером такого функтора, он преобразует тип a в тип Maybe a (сам по себе Maybe не является типом!):
Монады
Все функции, которые были рассмотрены до этого, были чистыми, т.е. предполагалось, что у них нет побочных эффектов. Это функции в математическом смысле: результат чистой функции зависит только от значения её аргумента, он не меняется из-за места или времени вызова.
Поставим перед собой задачу логгировать вызовы функций. На императивном языке проще всего было бы хранить лог как глобальное состояние, которое изменяется в теле каждой функции. Программирование на функциональных языках не располагает к использованию глобального состояния, поэтому будем решать поставленную задачу, оперируя имеющимися у нас чистыми функциями — морфизмами в категории типов языка Haskell.
Типы функций позволяют составить их композицию:
Чтобы не отвлекаться на сложности реализации, в качестве представления лога возьмём просто строку. Мы хотим, чтобы после применения функции processString в логе содержалась запись «upCase toWords».
Запись в лог — побочное действие функций, мало относящееся к их основному функционалу. Хотелось бы во-первых, добавить информацию на уровне типов о том, что будет выполняться логгирование, и во-вторых, минимизировать дополнительные действия, которые придётся проделать сторонним разработчикам для работы с этими функциями.
Создадим новый тип данных, который будет помимо самих значений типа a хранить ещё и строку, в которую каждая вызванная функция будет добавлять своё имя.
Заметим, что Writer — это функтор, мы легко можем описать для него функцию fmap :
Преобразуем функции upCase и toWords и сделаем так, чтобы они возвращали значение, «завёрнутое» в тип Writer :
Теперь мы больше не можем записать композицию этих функций так же, как раньше, из-за несоответствия типов. Определим специальную функцию для композиции, которая сначала получает значение типа b и первую строку, передаёт это значение второй функции, получает значение типа c и вторую строку и в качестве финального результата возвращает значение типа c и конкатенацию строк, полученных при вычислении:
Реализация функции processString принимает вид:
Для того, чтобы получить настоящую категорию с такими морфизмами, необходимо определить ассоциативную композицию морфизмов и тождественный морфизм для каждого объекта таким образом, чтобы соблюдались аксиомы теории категорий. Тогда полученная категория называется категорией Клейсли, а функтор m — монадой. На Haskell это определение выглядит так (везде далее используются типы из категории Hask):
Например, для типа Writer реализация будет следующей:
Мы пришли к третьему определению класса Monad :
Здесь присутствует явное требование на то, чтобы m был функтором. Это ограничение не было нужно для предыдущих определений, поскольку функция fmap реализуется через >>= :
Практическое применение монад
Приведём примеры практического применения монад для решения задач, которые традиционно решаются с использованием «нечистых» функций и побочных эффектов.
Недетерминированные вычисления
Абстракция недетерминированных вычислений (т.е. таких, у которых может быть несколько возможных результатов) реализуется с помощью списков.
Тогда оператор >>= можно записать так:
Резюмируем эти реализации в классическом определении класса Monad :
Конечно, список как результат функции не обязательно обозначает недетерминированность вычислений. Хорошим примером, когда это действительно так, является реализация искусственного интеллекта для игр. Список может представлять возможные результаты хода игрока, ответных ходов может быть тоже несколько — всё время приходится работать со списками, списками списков и т.д.
Исключения
Простейшая реализация обработки исключений в чистых функциях состоит в добавлении в тип возвращаемого значения специального варианта, обозначающего, что что-то пошло не так.
Определение методов класса Monad для Maybe :
Для классификации ошибок можно использовать перечислимый тип или любую другую структуру данных, подходящую для конкретной задачи. Мы в примерах продолжим использовать просто строку. Введём синоним типа для работы с исключениями:
Композиция функций описывается аналогично случаю с использованием Maybe :
Определение экземпляра класса Monad уже не должно вызывать трудностей:
Состояния
Объявим синоним типа для работы с состоянием:
Фиксируем тип состояния s и покажем, что State s является функтором. Нам понадобится вспомогательная функция runState :
Реализация класса Functor :
Конечно, в реализации Unit можно опустить. Здесь он добавлен для того, чтобы показать эту операцию с точки зрения теории категорий.
Тип IO — один из первых, о котором узнаёт начинающий пользователь Haskell, и наверняка сразу встречает пугающее слово «монада». Такой упрощённый взгляд на этот тип как на состояние для работы с внешним миром может помочь понять, почему это так. Кончено, это описание очень поверхностно, но полноценный рассказ о том, как на самом деле реализован ввод-вывод, зависит от компилятора и выходит далеко за рамки статьи.
Монады с точки зрения теории категорий
Мы начнём с простого введения в категории и функторы, затем дадим определение монады, приведём простые примеры монад в категориях и в конце приведём монадическую терминологию используемую в языках программирования.
Я уверен, что монады с точки зрения категорий почти элементарны.
Содержание
Категория
Категория состоит из объектов и морфизмов между ними. Термин «морфизм» не совсем корректен (он не обязан превращать что-то), по этому, часто, морфизм называют «стрелкой» для того, чтобы показать его абстрактную сущность.
Мы будем использовать термин «стрелка» во всех случаях, кроме того, когда стрелка обозначает некоторую функцию, тогда мы будем называть её «морфизм», но для меня он всё равно останется стрелкой.
Неважно, чем является объект или стрелка, важно только выполнение следующих свойств:
Замечание. В виду чрезвычайно абстрактной природы этой записи, мы не можем ожидать, что «все объекты» или «все стрелки из a к b» образуют множество. Категории, где они являются множествами называются «малые» или «локально малые».
Примеры категорий
Дополнительный материал
Образуют ли сами категории категорию? Да, но тогда нам следует дать определение стрелок между ними. Они являются стрелками второго порядка и называются функторами.
Функтор
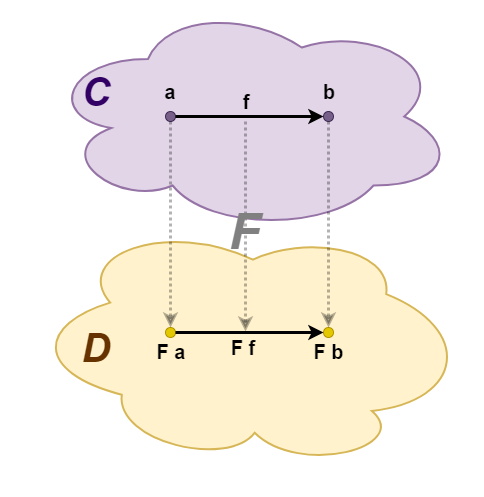
Функтор отображает одну категорию в другую. Для того, чтобы сделать это, нам нужно отобразить объекты из первой категории во вторую и стрелки (морфизмы) из первой категории в стрелки второй категории непротиворечивым образом.
Примеры функторов
Упражнение. Определите такое же расширение для частичных функций.
Естественное преобразование
По этому оно называется «естественным» — оно действует непротиворечиво с действиями функторов на стрелки.
Примеры естественных преобразований
Опять же, это определение можно записать следующим образом:
Монада
Примеры монад
Помните, что мы можем считать частично-упорядоченные множества и их функции, сохраняющие порядок, как категории и функторы?
Эти два условия являются ни чем иным, как аксиомами монад, применёнными к частично-упорядоченным множествам, считая, что монады в частично-упорядоченных множествах и есть замыкания. Также можно попытаться применить это к частично-упорядоченным множествам путей графа.
Монады исключения и состояния
Монада исключения
Монада состояния
Скучное упражнение. Докажите, что это действительно монада.
Монады в программировании
Преимущество такой модели состоит в том, что мы можем погрузить все наши высказывания относительно программ в очень стабильную теорию категорий; возможно менять сущность объектов и категорий, изменять логику лежащего в основе топоса и быть на 100% уверенными в том, о чем мы говорим. Например, вместо «нечёткой логики» можно использовать интуиционистскую логику или семнтику Крипке.
Кажется, что некоторые техники программирования не подходят для такой модели, например исключения или побочные эффекты.
А для функций имеющих состояние подойдёт, соответственно, монада состояния.
Монада IO в Haskell
В Haskell ввели монаду IO, чтобы избежать сложности с описанием того, каким образом функции могут иметь побочные эффекты.
Они использовали следующий трюк. Возьмите монаду состояния, как мы делали до этого. Вообразите, что A это множество состояний, представляющее внешний мир, а X это множество результатов функции.
Интересно, чего же конкретно они пытались этим добиться.