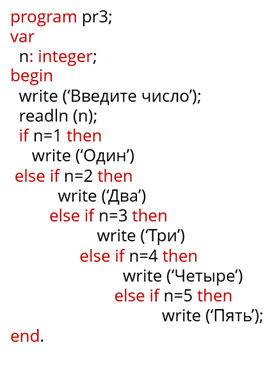Оператор ветвления
Оператор ветвления (условная инструкция, условный оператор) — оператор, конструкция языка программирования, обеспечивающая выполнение определённой команды (набора команд) только при условии истинности некоторого логического выражения, либо выполнение одной из нескольких команд (наборов команд) в зависимости от значения некоторого выражения.
Содержание
Общее описание
Оператор ветвления применяется в случаях, когда выполнение или невыполнение некоторого набора команд должно зависеть от выполнения или невыполнения некоторого условия. Ветвление — одна из трёх (наряду с последовательным исполнением команд и циклом) базовых конструкций структурного программирования.
Виды условных инструкций
Существует две основные формы условной инструкции, встречающиеся в реальных языках программирования: условный оператор (оператор if) и оператор многозначного выбора (переключатель, case, switch).
Условный оператор
Встречаются следующие формы условного оператора:
Условный оператор с одной ветвью
Реализация
Algol, Pascal
Algol-68, Ada, Modula-2
Необходимость условного оператора в Алголе и Паскале с момента появления была объектом критики. Критики говорили, что многочисленные составные операторы загромождают программу, мешают нормальной расстановке отступов и провоцируют ошибки (если в последней ветви оператора if забыть составной оператор там, где он необходим, то компилятор ничего не заметит, но при выполнении программы из группы операторов, которые должны выполняться в этой ветви, по условию будет выполняться только первый, все остальные — всегда). Следующие поколения языков — потомков Алгола попытались избавиться от этого недостатка. В их числе три широко известных языка: Алгол-68, Модула-2 и Ада. Конструкция оператора if в них практически одинакова, с точностью до отдельных ключевых слов:
Во всех случаях «командыX» — любое число операторов разделённых точкой с запятой. Во всех случаях все ветви условного оператора, кроме первой (ветви «then») необязательны и могут быть пропущены. Если ветвь «else» отсутствует и ни одно из условий не выполняется, то управление передаётся на команду, следующую за ключевым словом завершения условной конструкции (END, FI или END IF).
C, C++ и их потомки
C и C++ (а вслед за ними и Java, C#, PHP и множество других языков) имеют условный оператор, структурно аналогичный Паскалю. Отличие состоит в том, что условие должно быть записано в круглых скобках, а вместо ключевых слов begin и end используются фигурные скобки <> :
Nemerle
Forth
Здесь просто помещает значение на вершину стека, IF анализирует флаг, и если:
При отсутствии ELSE получается селектор с одной ветвью: выражения между IF и THEN выполняются только при ненулевом значении флага.
Fortran
Fortran изначально имел только арифметический IF, в котором в зависимости от знака выражения производился переход на одну из трёх меток. Например, часть кода подпрограммы решения квадратного уравнения:
Затем были добавлены логические (булевские) выражения и логический IF с одним оператором, вычисляемый GOTO, позже — структурный IF (с несколькими условиями), например:
Perl поддерживает структурный if с несколькими условиями, а также модификаторы оператора (statement modifiers), которые записываются после выполняемой части оператора. Например, два следующих примера идентичны по функциональности:
Вместо if можно писать unless, что приводит к инверсии значения условного выражения перед проверкой. То же самое действие через unless:
Для составного оператора (блока) допустима только структурная форма, но не модификатор. Например:
Завершающее ключевое слово не нужно, за счёт требования обязательного оформления операторов под условиями в блоки <…>.
Не существует аналога слова unless для веток elsif.
Erlang
Erlang использует два условных оператора — if и case. Оба имеют результирующее значение, которое равно значению последнего оператора в выполненной ветке и может быть использовано (назначено имени, передано в функцию…), поэтому в нём нет отдельного тернарного условного оператора. В операторе case выполняется Сопоставление с образцом, с возможностью дополнительных условий на значения в сравниваемом, а в операторе if — только проверка условий. В условиях (guard tests) допускается ограниченное множество операций и встроенных функций.
Пример на case (удаление записи о событии из дерева времён):
Переключатель
Конструкция переключателя имеет несколько (две или более) ветвей. Переключатель выполняет одну заданную ветвь в зависимости от значения вычисляемого ключевого выражения. Принципиальным отличием этой инструкции от условного оператора является то, что выражение, определяющее выбор исполняемой ветви, возвращает не логическое, а целое значение, либо значение, тип которого может быть приведён к целому. В некоторых языках допускается использовать в переключателе выражения некоторых типов, не приводимых к целому (например, текстовые строки).
Прототипом современной синтаксической конструкции была используемая в старых языках программирования команда перехода по вычисляемой метке. В этой команде указывалось выражение-селектор, возвращающее целое значение, и набор меток. При выполнении команды вычислялось выражение, а его значение использовалось как номер метки (в списке команды), на которую производился переход. Такие конструкции были, например, в языках программирования Фортран («вычисляемый GOTO») и Бейсик. Привлекательной стороной конструкции является её достаточно высокая эффективность: для определения нужной ветви (метки перехода) не требуется последовательно сравнивать результат выражения-селектора со многими занчениями, достаточно записать в память массив команд безусловного перехода с нужными адресами, чтобы при выполнении команды вычислять нужный элемент непосредственно из значения выражения. При этом скорость выполнения команды не зависит от количества меток. В современных языках реализация оператора-переключателя также часто выполняется в виде таблицы перехода, состоящей из команд безусловного перехода на соответствующие фрагменты кода. Вычисляемое выражение преобразовывается в значение сдвига по таблице перехода, определяющее выполняемую команду. В языках, где выражение-селектор может иметь нецелое значение, напрямую вычислить нужную ветвь конструкции переключателя можно далеко не всегда, поэтому в них используются другие методы оптимизации исполнения.
Например, в языке Си синтаксис команды следующий:
Синтаксис команды-переключателя Си унаследован множеством языков, но семантика его не всегда полностью аналогична Си. Например, в C# допускается использовать выражение-селектор строкового типа и соответствующие метки.
Особенности вычисления логических выражений
На порядок исполнения программы с условными операторами может существенно влиять принятая в языке логика вычисления условных выражений. Когда условие представляет собой сложное логическое выражение, к примеру «f(x) > 0 И g(y) > 0», существует две стратегии вычисления его результата:
Второй вариант является наиболее распространённым для промышленных языков (в частности, для Алгола, Фортрана, С++, С, Java, JavaScript, ECMAScript, JScript, C#, Python). В этих языках действует жёсткое правило: «Логическое выражение всегда вычисляется слева направо и его вычисление останавливается сразу же, как только результат всего выражения становится определённым». Это означает, что если выражение состоит из нескольких подусловий, объединённых оператором «И» (AND), то вычисление выражения прекратится, как только одно из подусловий окажется ложным (так как «ложь AND любое значение» в результате всегда даёт «ложь»), и, наоборот, если несколько подусловий объединены оператором «ИЛИ» (OR), вычисление прекратится после первого же истинного подусловия, поскольку в этом случае всё выражение истинно, независимо от дальнейших вычислений. А вот выражение, содержащее оператор «Исключающее ИЛИ» (XOR) неполному вычислению не поддаётся, поскольку в нём одно из значений не может определить результат вычисления всего выражения.
Языки Ада и Erlang используют разные ключевые слова для этих вариантов: слова and и or означают полное вычисление, а and then, or else (Ада), andalso, orelse (Erlang) — неполное. В Erlang andalso и orelse менее приоритетны, чем операции сравнения, что позволяет избежать скобок вокруг элементарных условий.
Фиксированный порядок вычисления подусловий (логическое выражение всегда вычисляется слева направо) вводится для того, чтобы иметь возможность управлять порядком вычисления выражения и помещать в него сначала те условия, которые должны вычисляться в первую очередь. Этим, кстати, логические выражения отличаются арифметических, для которых, в большинстве языков, порядок вычисления подвыражений (если только он не определён приоритетом и ассоциативностью операций) языком не задаётся и в разных случаях может быть различным.
Выбор именно такой логики исполнения связан с тем, что она позволяет упростить логические выражения, в которых используются зависимые элементы. Классический пример — линейный поиск в массиве:
Алгоритм, реализуемый программой, совершенно очевиден, но в реализации есть одна тонкость (см. строку, помеченную восклицательными знаками): условие цикла состоит из двух частей, связанных оператором AND. Первое подусловие проверяет, не вышел ли индекс i за пределы массива, второе — не равен ли текущий элемент массива искомому значению. Если массив не содержит искомого значения, то после проверки последнего элемента значение переменной i увеличится на единицу; на следующей итерации первое подусловие окажется ложным и цикл завершится без проверки второго подусловия. Если бы логические выражения вычислялись полностью, то при отсутствии искомого элемента в массиве после последней итерации происходила бы ошибка: попытка определить a[i] вызывала бы некорректное обращение к памяти.
Следует обратить внимание, что, кроме неполного вычисления значения выражения, здесь также играет существенную роль фиксированный порядок вычисления подусловий: поскольку проверка выхода за границу массива записана первой, она всегда будет выполняться раньше, чем проверка достижения искомого значения. Если бы порядок вычисления подвыражений был неопределённым, гарантировать правильность приведённого фрагмента программы было бы невозможно.
При полном вычислении логических выражений приведённый алгоритм пришлось бы записать примерно в следующем виде:
Как видим, пришлось искусственно задать порядок вычисления условий выхода и ввести дополнительную переменную. Именно для того, чтобы избежать подобных трюков, и введено неполное вычисление логических выражений.
Примечание: Код изложенный выше, является примером использования оператора IF но не более. Этот код нельзя использовать как правило для написания алгоритмов на языке Паскаль.
Ниже приведен оптимальный алгоритм для поиска числа в массиве:
Конструкция ветвления в C++ и операторы if/else: правильное применение
Любая компьютерная программа подразумевает ветвление. Это ситуация, когда нужно выбрать тот или иной вариант в зависимости от условий. Например, если некий результат вычислений меньше 100 — нужно вывести сообщение «Результат не дотягивает до сотни». Если больше — выводится «Результат превышает сотню и потрясающе выглядит».
Для этого в C++ есть так называемые операторы ветвления — особые команды, которые показывают компилятору, что можно выбирать из тех или иных вариантов. Сегодня мы поговорим о том, какие есть операторы ветвления в C++, как они функционируют, также приведем примеры их использования.
Конструкция ветвления в C++. Операторы условного ветвления if/else
Сфера применения операторов ветвления в C++ и других языках программирования крайне широка. С их помощью реализуется очень много задач, они позволяют изучить логику программирования и понять, как это все работает. Грубо говоря, эти операторы универсальны по своему значению и применяются везде.
Нажали одну кнопку — система выдала определенный результат на основании данных на входе. Нажали другую — система выдала иной результат на основании тех же входных данных. Не нажали, но прошло определенное время по таймеру — будет третий результат.
Само собой, это умозрительный пример ветвления, но, надеюсь, идею вы поняли. Давайте перейдем к практической стороне реализации.
Блок-схема простейшего варианта ветвления выглядит следующим образом:
Скриншот с bookflow.ru
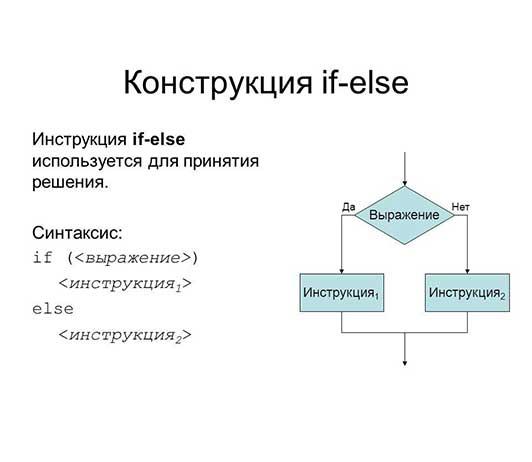
Здесь все просто и понятно: если выражение принимает положительное значение — выполняется одна инструкция. Отрицательное — другая. В качестве наглядного примера возьмем вот такую небольшую программу на С++. В ней надо ввести любое произвольное число, которое может быть меньше 100, или же больше/равно 100.
Здесь, как видим, реализован простейший вариант — проверка идет по принципу больше/меньше. Помимо этого, никаких проверок. Ниже мы рассмотрим вариант, когда программа будет различать более точные вводные данные — меньше, больше или равно.
Само собой, эта простейшая программа не включает проверку корректности символов — туда можно ввести любые данные — цифры, буквы, символы из ASCII и так далее. Однако корректные результаты получить можно будет только на цифрах.
Использование нескольких операций в ветвлениях if/else
Бывает так, что нужно выбрать не из двух, а из большего числа вариантов — трех и так далее. Давайте посмотрим, как это можно сделать:
Мы добавили новое условие, которое позволяет уточнить результат — число строго больше 100 или строго равно ему. Как видите, ничего сложного. Это также называется связыванием стейтментов.
Вложенные ветвления if/else
Еще один способ сломать себе мозг осуществить выбор в программе — вложенные ветвления. Суть понятна из названия — внутри одной пары if/else есть другая или другие пары. Выглядит это логически примерно так:
Скриншот с bookflow.ru
Строго говоря, это ничем не отличается от обычного ветвления, разве что только для выполнения внешнего условия сначала должно выполниться внутреннее (вложенное).
И вот здесь надо быть внимательным, поскольку количество if и else должно быть одинаковым — как и фигурных скобок. Иначе говоря, оператор else всегда относится только к последнему незакрытому оператору if в том же блоке.
Для улучшения читабельности кода желательно использовать те самые фигурные скобки, чтобы не запутаться. Они не окажут влияния на работу программы или компилятора, однако помогут визуально улучшить код сам по себе.
Неявное указание блоков if/else
Таким образом, блок кода…
…превращается в такую конструкцию:
С точки зрения компилятора ничего не поменялось — логика та же самая, только изменилось написание. Это можно сравнить с синонимами в естественном языке — допустимо, но не обязательно, и не влияет на восприятие в целом.
Нулевые стейтменты
Пример неправильного кода:
Здесь мы закрыли оператор if с помощью точки с запятой, то есть фактически дополнили его нулевым стейтментом. В этом случае программа будет выполняться неверно, поскольку проверка, равна ли переменная a нулю, уже не проводится. Тут переменная получит значение 1 в любом случае.
А вот правильный код:
Вывод
В статье мы рассмотрели самые простые варианты ветвления и только для одного языка, хотя алгоритм работает аналогично и в других — разница только в синтаксисе. Конечно, есть и другие операторы ветвления даже в самом C++ — тот же весьма мощный по своим возможностям оператор switch или «переключатель». Его работу можно увидеть в так называемых «радиокнопках» в интерфейсе многих программ. Его специфика: он удобен при обработке множества опций выбора, там можно выбрать только один вариант.
К слову, то же самое, что было в статье, но более подробно, есть в этом тематическом видео:
Что такое ветвление в программировании
Условный оператор. Формат условного оператора следующий:
if (выражение) оператор1; else оператор2;
Это полная форма оператора, программирующая структуру полного ветвления. Обычно выражение — это некоторое условие, содержащее операции отношения и логические операции. Значение выражения приводится к целому и интерпретируется в соответствии с правилом: равно нулю — ложь, не равно нулю — истина. Если выражение истинно, выполняется оператор 1, если ложно — оператор 2.
Необходимо обратить внимание на следующие особенности синтаксиса условного оператора:
• выражение записывается в круглых скобках;
• точка с запятой после оператора 1 ставится обязательно.
Возможно использование неполной формы условного оператора
if (выражение) оператор;
Вот пример использования полной формы условного оператора для нахождения большего значения из двух переменных а и b :
if(a>b) max=a; else max=b;
Та же самая задача может быть решена с использованием неполного ветвления следующим образом:
Пример 2. Алгоритм с неполным ветвлением:
Пример 3. Упорядочить по возрастанию значения в двух переменных а, b:
В данном примере использован составной оператор — последовательность операторов, заключенная в фигурные скобки. В С фигурные скобки выполняют роль операторных скобок по аналгии с Begin, End в Паскале.
Обратите внимание на то, что перед закрывающей фигурные скобкой точку с запятой надо ставить обязательно, а после скобки точка с запятой не ставится.
Программирование ветвлений
Урок 22. Информатика 10 класс (ФГОС)
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Программирование ветвлений»
На этом уроке мы с вами вспомним, как записывается условный оператор и оператор выбора на языке программирования Pascal, а также решим несколько задач с использованием этих структур.
В начале урока давайте вспомним, что такое ветвление.
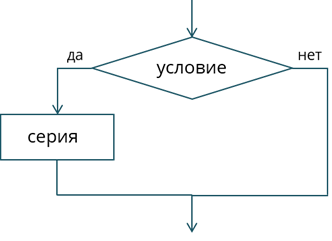
Ветвление – это алгоритмическая конструкция, при помощи которой происходит выбор одной из двух серий действий с выходом на общее продолжение. Давайте рассмотрим блок-схему полного ветвления.
Исходя из неё, мы видим, что, если условие является истинным, то выполняется серия 1, если же нет, то серия 2. Условие, в данном случае, это утверждение, которое может быть либо истинным, либо ложным. То есть условие – это логическое выражение. Теперь рассмотрим блок-схему неполного ветвления.
Если условие истинно, то выполняется серия, а если нет, то ничего не происходит.
В языке программирования Pascal такая структура записывается следующим образом:
В полной форме, если логическое выражение истинно, то выполняется оператор 1 (после then), в обратном случае – оператор 2 (после else).
В неполном ветвлении если логическое выражение истинно, то выполняется оператор, а если ложно, то программа переходит к следующей команде.
Обратите внимание, что при записи оператора ветвления в алгоритм, после «Если» используется условие, а вот при записи на языке программирование, будет записано логическое выражение, которое вычисляется в первую очередь.
В качестве оператора может быть, как одна команда, так и несколько. В случае, если команд несколько, стоит заключать их в операторные скобки begin…end.
А сейчас давайте напишем несколько программ.
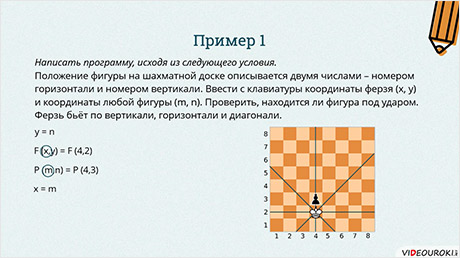
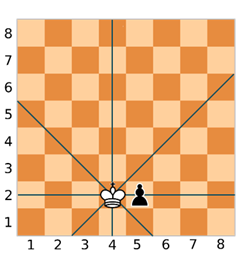
Пример 1. Написать программу, исходя из следующего условия: Положение фигуры на шахматной доске описывается двумя числами – номером горизонтали и номером вертикали. Ввести с клавиатуры координаты ферзя (x, y) и координаты любой фигуры (m, n). Проверить, находится ли фигура под ударом. Ферзь бьёт по вертикали, горизонтали и диагонали. Координаты ферзя и пешки не должны совпадать.
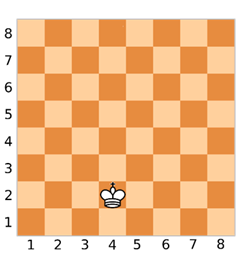
Прежде, чем составлять программу, давайте разберёмся при помощи рисунка.
Итак, у нас изображена шахматная доска. Пусть ферзь будет находится в клетке с координатами (4, 2).
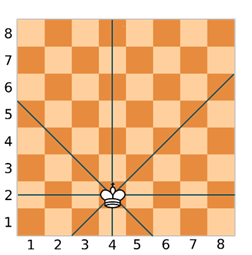
Нарисуем прямые линии, по которым может ходить ферзь. То есть нарисуем горизонтальную, вертикальную и две диагональных линии.
Давайте возьмём любую фигуру, например, пешку, и поставим её, например, в клетку, с координатами (5, 2).
Мы можем видеть, что наша фигура находится под ударом. Помимо этого, у ферзя и пешки совпадают вторые точки координат, то есть y = n. Это будет первым условием, когда фигура будет находиться под ударом ферзя по горизонтали.
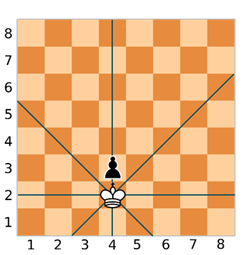
По вертикали фигура будет находится под ударом в том случае, если у ферзя и пешки будут совпадать первые точки координат, то есть если x = m. Давайте поставим пешку в клетку с координатами (4, 3).
Мы видим, что она находится под ударом. Это будет вторым условием.
Ферзь ещё может ходить по диагонали. Здесь также есть своя закономерность для того, чтобы узнать, находится ли фигура под ударом. Для этого нужно сравнить модули разности x–m и y–n. Если они равны, то фигура находится под ударом ферзя.
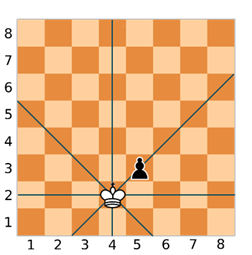
Давайте проверим. Поставим пешку в клетку с координатами (5, 3). Как мы помним, ферзь стоит в клетке с координатами (4, 2).
Вычислим |x–m|. Он будет равен 1. Также вычислим |y–n|. Он будет также равен 1. Соответственно модули разности равны, и фигура находится под ударом.
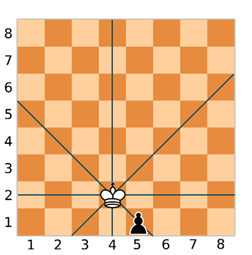
Теперь давайте проверим другую диагональ. Поставим фигуру в клетку с координатами (5, 1).
При вычислении модулей разности получим, что они равны 1. Соответственно фигура снова находится под ударом.
А сейчас давайте перейдём непосредственно к написанию программы.
Зададим имя программы z1, то есть задание 1. Далее объявим 4 переменных x, y, m, n целого типа integer.
После слова begin организуем диалог между пользователем и компьютером. Пишем Write, а в скобках и одинарных кавычках попросим ввести координаты для ферзя (x, y). Присвоим соответствующим переменным значения, введённые с клавиатуры при помощи операции Read.
Аналогично поступим и с вводом с клавиатуры координат для фигуры. Скопируем две функции Write и Read и изменим их для ввода данных новой фигуры. В операторе Read считаем значения переменным m и n.
Теперь нам нужно записать условие. Мы с вами помним, что у нас 3 логических выражения и, при выполнении хотя бы одного из них, наша фигура будет находится под ударом. Поэтому запишем их при помощи дизъюнкции, то есть будем использовать союз or.
Далее идёт служебное слово then В случае, если хотя бы одно из условий выполняется, наша фигура будет находится под ударом. Значит здесь мы должны вывести соответствующее сообщение:
Write (‘Фигура находится под ударом’)
Точку с запятой в конце не ставим, так как мы с вами будем использовать полную форму ветвления, а перед else точка с запятой не ставятся.
Write (‘Фигура не находится под ударом’)
Завершаем нашу программу.
Для проверки будем использовать координаты, которые мы с вами проверяли при помощи рисунка.
Итак, координаты ферзя – (4, 2). Координаты пешки – (5, 2).
Фигура находится под ударом.
Далее введём всё те же координаты для ферзя, а для пешки зададим координаты (5, 3).
И снова получаем верный результат.
А сейчас давайте возьмём координаты, при которых пешка не будет находится под ударом. Например, (6, 1).
И снова мы получили верный результат. Значит задача решена верно.
Рассмотрим ещё один пример. Составить блок-схему и написать программу для решения геометрической задачи. Определите, является ли треугольник со сторонами a, b, c равнобедренным. Если да, то укажите, что является основанием, а что – боковыми сторонами.
Прежде чем приступать к решению, давайте вспомним, что такое равнобедренный треугольник. Равнобедренный треугольник – это треугольник, в котором две стороны равны между собой. Таким образом, если наш треугольник равнобедренный, то a должно быть равно b, или же a равно c, или b равно c.
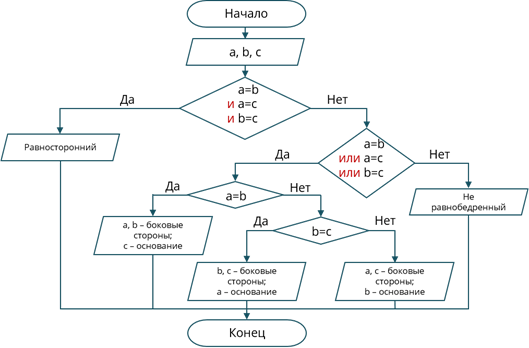
Давайте составим блок-схему.
Начало. Затем идёт ввод переменных a, b и c. Далее идёт блок условия, в котором мы будем проверять, равны ли все 3 стороны между собой. Если да, то треугольник является равносторонним и соответственно будет идти блок вывода на экран соответствующей информации. Если же 3 стороны не равны между собой, то будет снова идти блок условия, в котором будет проверятся, равны ли между собой хотя бы 2 из сторон. Если нет и все 3 стороны разные, то будет идти блок вывода информации, что треугольник не является равнобедренным. Если же условие будет выполняться, то снова будет идти блок условия, в котором будем проверять следующее: a = b. Если да, то будет идти блок вывода на экран со следующим сообщением: a и b – боковые стороны треугольника, c – основание. Если же условие a = b ложно, то будет идти очередной блок условия, в котором будет проверять следующее: b = с. Если условие истинно, то будет идти блок вывода информации со следующим текстом: b, c –боковые стороны треугольника, a – основание. Если условие b = c – ложно, то будет идти блок вывода информации: a, c – боковые стороны треугольника, b – основание.
В конце от всех блоков вывода информации будут идти линии к блоку конца программы.
А сейчас давайте напишем программу.
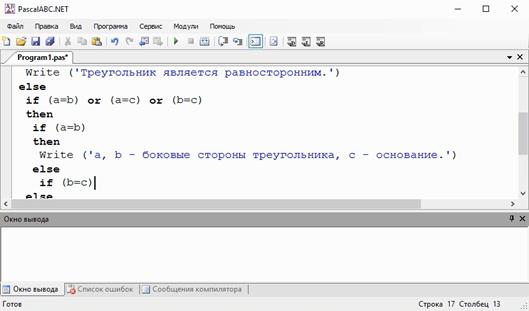
Объявляем 3 переменных a, b, c вещественного типа, так как стороны треугольника могут быть равны вещественным числам. После begin Выведем на экран следующее сообщение: «Введите три стороны треугольника через пробел в следующем порядке: a, b, c.». Функцией Read зададим соответствующим переменным введённые значения. Далее будет идти условный оператор if, с помощью которого мы с вами проверим, равны ли все 3 стороны между собой. Это будет записано так:
(a = b) and (a = c) and (b = c)
Если условие истинно, то после then будет идти операция вывода:
Write (‘Треугольник является равносторонним’)
Если же условие ложно, то после else будет идти ещё один условный оператор if, в котором мы проверим, равны ли между собой хотя бы две стороны треугольника. Запишем then и перейдём на новую строку.
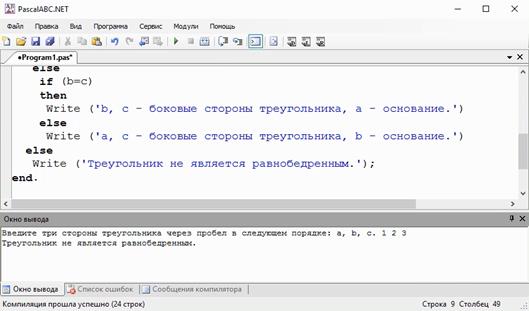
else. Давайте сначала запишем, что будет, если условие ложно. То есть после else запишем функцию
Write (‘Треугольник не является равнобедренным.’);
Вернёмся к условию. Если 2 стороны треугольника равны, то нужно выяснить какие, поэтому после then запишем условный оператор, при помощи которого проверим следующее: a = b. Если условие истинно, то после then пишем функцию
Write (‘a, b – боковые стороны треугольника, c – основание.’)
Если условие a = b ложно, то снова при помощи условного оператора if проверим стороны b и c.
Если они равны, то на экран будет выводиться сообщение
Write (‘b, c – боковые стороны треугольника, a – основание.’)
Если условие b = c – ложно, то на экран снова выведем сообщение
Нам осталось завершить программу. Пишем в конце end с точкой.
А теперь давайте проверим программу. Запускаем её и введём три единицы.
Такой треугольник является равносторонним, и мы получили соответствующее сообщение от программы.
А сейчас проверим, если все стороны не равны.
На экран выводится сообщение о том, что треугольник не является равнобедренным.
А сейчас поочерёдно проверим случаи, если a = b, b = c и a = c.
Программа работает верно.
В языке программирования Pascal существует оператор выбора case. Рассмотрим его формат записи в полной и неполной формах:
В этих записях «селектор» – это выражение любого порядкового типа; «константа» – постоянная величина того же типа, что и «селектор»; «оператор» – любой простой или составной оператор.
Давайте разберёмся на примере. Преобразовать введённое целое число из диапазона от 1 до 5 в его словесное представление.
Этот пример можно решить двумя способами: при помощи условного оператора или же оператора выбора.
Мы видим, что писать такую программу при помощи условного оператора скучно и однообразно. Давайте напишем эту же программу с использованием составного оператора.
Итак, начало программы будет таким же, как и при использовании условного оператора, включая функцию Read. Далее будет идти оператор case n of. Запишем все варианты наших чисел. Если введено число 1, то на экране должно появиться соответствующее сообщение. Записывается следующим образом:
Таким же образом расписываются и остальные 4 варианта.
Если же введено число, не входящее в наш диапазон, то выведем сообщение, в котором будет указано, что введено другое число. То есть после else запишем функцию Write и соответствующий текст. Завершим оператор выбора словом end и точка с запятой. После этого завершим всю программу.
Запустим её и проверим.
Программа работает верно.
А теперь давайте разберёмся, как она работает.
Сначала вычисляется выражение-селектор, то есть программа смотрит, чему равно n. Далее в списках констант ищется такое значение, которое совпадает с полученным значением селектора, то есть ищет число, равное n. После этого выполняется оператор, помеченный данной константой. В нашем случае выводится на экран словесное представление числа. Если же такой константы нет, то происходит переход к выполнению оператора, следующего после слова else. То есть если, введено число, не принадлежащее к нашему диапазону, то на экран будет выведено сообщение, что введено другое число.
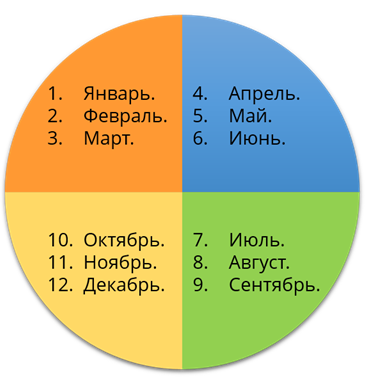
Давайте составим программу, исходя из следующего условия: определить номер квартала по введённому номеру месяца.
Прежде чем приступать к написанию программы, давайте вспомним, что в году 4 квартала. В каждом квартале по 3 месяца. То есть первый квартал включает в себя первый, второй и третий месяца; Второй – четвёртый, пятый и шестой месяца; и так далее.
Приступим к написанию программы.
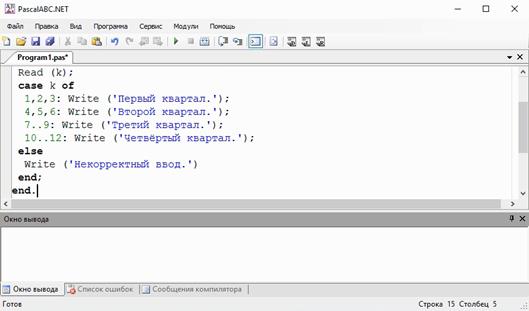
Объявим переменную k целого типа. Далее, после begin, организуем диалог между пользователем и компьютером и попросим ввести номер месяца. Считаем его при помощи функции Read. Теперь запишем сам оператор выбора: case k of.
Далее перечислим номера первый трёх месяцев через запятую, а после двоеточия запишем функцию вывода
Write (‘Первый квартал.’);
На следующей строчке пишем номера месяцев, которые входят во второй квартал и выводим на экран соответствующий текст.
Далее запишем следующее:
7..9: Write (‘Третий квартал’);
Такая запись указывает диапазон чисел. В нашем случае в него будут входить числа 7, 8 и 9.
Запишем аналогичным образом строку для 4 квартала.
После else у нас будет идти оператор вывода со следующим текстом
Write (‘Некорректный ввод.’);
Завершим оператор вывода:
Завершим всю программу.
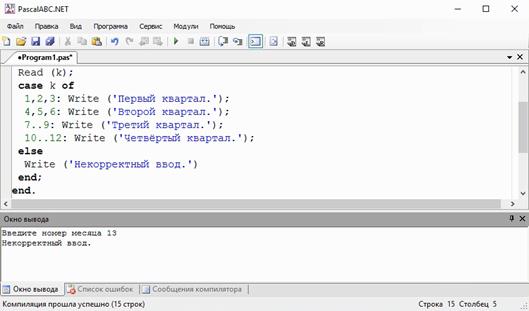
Программа работает верно.
Пришла пора подвести итоги урока. Сегодня мы с вами вспомнили как выглядят и работают условный оператор и оператор выбора. Также решили несколько задач с использованием этих операторов.