Типизация языков программирования: разбираемся в основах
Авторизуйтесь
Типизация языков программирования: разбираемся в основах
Типизация языков программирования — это то, как различные языки распознают типы переменных. Она определяет, как вы будете работать с типами переменных: нужно ли их задавать изначально, можно ли изменять и так далее.
Виды типизации
Языки программирования бывают типизированными и нетипизированными (бестиповыми).
Бестиповая типизация в основном присуща старым и низкоуровневым языкам программирования, например Forth. Все данные в таких языках считаются цепочками бит произвольной длины и, как следует из названия, не делятся на типы. Работа с ними труднее, и при чтении кода не всегда ясно, о каком типе переменной идет речь. Это можно исправить, написав комментарии к коду.
При этом у нетипизированных языков немало плюсов. В них можно совершать операции с любыми данными, и код получается более эффективным.
Перейдём к типизированным языкам.
Статическая и динамическая типизация
Особенность языков программирования со статической типизацией в том, что проверка типов начинается на стадии компиляции. Компиляторы ищут ошибки ещё до запуска программы, и вам не нужно раз за разом запускать её, чтобы выяснить, что пошло не так. Благодаря этому статически типизированные языки программирования зачастую быстрее. Кроме того, тип для переменной можно назначить только один раз. Например в Java такая запись вызовет ошибку на этапе компиляции:
В свою очередь, языки с динамической типизацией ищут ошибки на стадии исполнения. В них можно задать разные типы для одной и той же переменной, и они более гибкие. Например, в Python возможна такая запись, и ошибки не будет:
Сильная и слабая типизация
В слабо типизированных языках программирования можно смешивать разные типы данных. Так код получается короче — язык «старается» сам выполнять операции преобразования с разными типами. Впрочем, в таком случае не всегда ясно, как поведёт себя программа. Например, в JavaScript возможна такая запись:
При сильной или строгой типизации, как в Python, язык не позволяет смешивать разные типы — то есть, если вы обозначили переменную как число, то добавить к ней строку уже не получится:
Языки с сильной типизацией надёжнее. Да и программист, прописывая все преобразования вручную, лучше понимает, как работает его код.
Явная и неявная типизация
В языках программирования с явной типизацией типы переменных и возвращаемых значений функций нужно задавать. Это дольше, но так проще определять, что значат все данные, а программисту не придётся запоминать или записывать отдельно каждое значение. В языке С переменную нужно записывать так:
При неявной типизации тип переменной определяется интерпретатором или компилятором, поэтому записи в таких языках короче. Иногда они позволяют вручную указывать типы значений, как в Haskell или Python. В Python возможна такая запись, ведь язык сам определит, что это целое число:
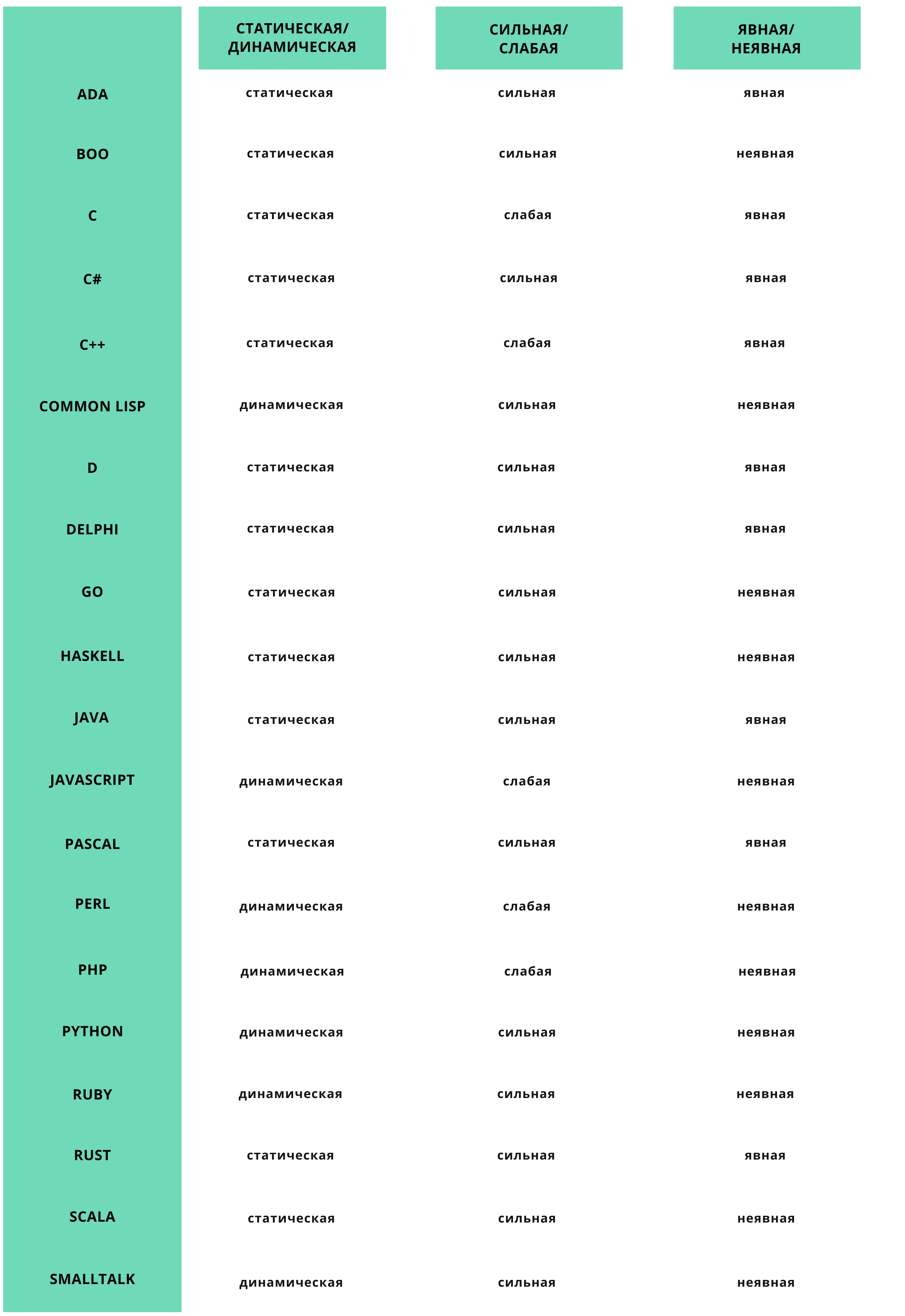
Типизация в разных языках программирования
Разные категории могут пересекаться. Обычно языку программирования присуще одно значение из каждой группы: он может быть сильным или слабым, явным или неявным. Но есть несколько исключений. Так, Python с аннотациями может поддерживать явную типизацию, а язык D, наоборот, — неявную. С# поддерживает динамическую типизацию благодаря ключевым словам dynamic и var, Delphi — благодаря типу Variant, а С++ — с помощью библиотеки Boost и имеет одновременно черты языка с сильной и
слабой типизацией.
Ликбез по типизации в языках программирования
Эта статья содержит необходимый минимум тех вещей, которые просто необходимо знать о типизации, чтобы не называть динамическую типизацию злом, Lisp — бестиповым языком, а C — языком со строгой типизацией.
В полной версии находится подробное описание всех видов типизации, приправленное примерами кода, ссылками на популярные языки программирования и показательными картинками.
Рекомендую прочитать сначала краткую версию статьи, а затем при наличии желания и полную.
Краткая версия
Языки программирования по типизации принято делить на два больших лагеря — типизированные и нетипизированные (бестиповые). К первому например относятся C, Python, Scala, PHP и Lua, а ко второму — язык ассемблера, Forth и Brainfuck.
Так как «бестиповая типизация» по своей сути — проста как пробка, дальше она ни на какие другие виды не делится. А вот типизированные языки разделяются еще на несколько пересекающихся категорий:
Примеры:
Статическая: C, Java, C#;
Динамическая: Python, JavaScript, Ruby.
Примеры:
Сильная: Java, Python, Haskell, Lisp;
Слабая: C, JavaScript, Visual Basic, PHP.
Примеры:
Явная: C++, D, C#
Неявная: PHP, Lua, JavaScript
Также нужно заметить, что все эти категории пересекаются, например язык C имеет статическую слабую явную типизацию, а язык Python — динамическую сильную неявную.
Тем-не менее не бывает языков со статической и динамической типизаций одновременно. Хотя забегая вперед скажу, что тут я вру — они действительно существуют, но об этом позже.
Подробная версия
Если краткой версии Вам показалось недостаточно, хорошо. Не зря же я писал подробную? Главное, что в краткой версии просто невозможно было уместить всю полезную и интересную информацию, а подробная будет возможно слишком длинной, чтобы каждый смог ее прочесть, не напрягаясь.
Бестиповая типизация
В бестиповых языках программирования — все сущности считаются просто последовательностями бит, различной длины.
Бестиповая типизация обычно присуща низкоуровневым (язык ассемблера, Forth) и эзотерическим (Brainfuck, HQ9, Piet) языкам. Однако и у нее, наряду с недостатками, есть некоторые преимущества.
Преимущества
Недостатки
Сильная безтиповая типизация?
Да, такое существует. Например в языке ассемблера (для архитектуры х86/х86-64, других не знаю) нельзя ассемблировать программу, если вы попытаетесь загрузить в регистр cx (16 бит) данные из регистра rax (64 бита).
mov cx, eax ; ошибка времени ассемблирования
Так получается, что в ассемлере все-таки есть типизация? Я считаю, что этих проверок недостаточно. А Ваше мнение, конечно, зависит только от Вас.
Статическая и динамическая типизации
Главное, что отличает статическую (static) типизацию от динамической (dynamic) то, что все проверки типов выполняются на этапе компиляции, а не этапе выполнения.
Некоторым людям может показаться, что статическая типизация слишком ограничена (на самом деле так и есть, но от этого давно избавились с помощью некоторых методик). Некоторым же, что динамически типизированные языки — это игра с огнем, но какие же черты их выделяют? Неужели оба вида имеют шансы на существование? Если нет, то почему много как статически, так и динамически типизированных языков?
Преимущества статической типизации
Преимущества динамической типизации
Обобщенное программирование
Хорошо, самый важный аргумент за динамическую типизацию — удобство описания обобщенных алгоритмов. Давайте представим себе проблему — нам нужна функция поиска по нескольким массивам (или спискам) — по массиву целых чисел, по массиву вещественных и массиву символов.
Как же мы будем ее решать? Решим ее на 3-ех разных языках: одном с динамической типизацией и двух со статической.
Алгоритм поиска я возьму один из простейших — перебор. Функция будет получать искомый элемент, сам массив (или список) и возвращать индекс элемента, или, если элемент не найден — (-1).
Динамическое решение (Python):
Как видите, все просто и никаких проблем с тем, что список может содержать хоть числа, хоть списки, хоть другие массивы нет. Очень хорошо. Давайте пойдем дальше — решим эту-же задачу на Си!
Статическое решение (Си):
Ну, каждая функция в отдельности похожа на версию из Python, но почему их три? Неужели статическое программирование проиграло?
И да, и нет. Есть несколько методик программирования, одну из которых мы сейчас рассмотрим. Она называется обобщенное программирование и язык C++ ее неплохо поддерживает. Давайте посмотрим на новую версию:
Статическое решение (обобщенное программирование, C++):
Хорошо! Это выглядит не сильно сложнее чем версия на Python и при этом не пришлось много писать. Вдобавок мы получили реализацию для всех массивов, а не только для 3-ех, необходимых для решения задачи!
Эта версия похоже именно то, что нужно — мы получаем одновременно плюсы статической типизации и некоторые плюсы динамической.
Здорово, что это вообще возможно, но может быть еще лучше. Во-первых обобщенное программирование может быть удобнее и красивее (например в языке Haskell). Во-вторых помимо обобщенного программирования также можно применить полиморфизм (результат будет хуже), перегрузку функций (аналогично) или макросы.
Статика в динамике
Также нужно упомянуть, что многие статические языки позволяют использовать динамическую типизацию, например:
Сильная и слабая типизации
Языки с сильной типизацией не позволяют смешивать сущности разных типов в выражениях и не выполняют никаких автоматических преобразований. Также их называют «языки с строгой типизацией». Английский термин для этого — strong typing.
Слабо типизированные языки, наоборот всячески способствуют, чтобы программист смешивал разные типы в одном выражении, причем компилятор сам приведет все к единому типу. Также их называют «языки с нестрогой типизацией». Английский термин для этого — weak typing.
Слабую типизацию часто путают с динамической, что совершенно неверно. Динамически типизированный язык может быть и слабо и сильно типизирован.
Однако мало, кто придает значение строгости типизации. Часто заявляют, что если язык статически типизирован, то Вы сможете отловить множество потенциальных ошибок при компиляции. Они Вам врут!
Язык при этом должен иметь еще и сильную типизацию. И правда, если компилятор вместо сообщения об ошибке будет просто прибавлять строку к числу, или что еще хуже, вычтет из одного массива другой, какой нам толк, что все «проверки» типов будут на этапе компиляции? Правильно — слабая статическая типизация еще хуже, чем сильная динамическая! (Ну, это мое мнение)
Так что-же у слабой типизации вообще нет плюсов? Возможно так выглядит, однако несмотря на то, что я ярый сторонник сильной типизации, должен согласиться, что у слабой тоже есть преимущества.
Хотите узнать какие?
Преимущества сильной типизации
Преимущества слабой типизации
Оказывается есть и даже два.
Неявное приведение типов, в однозначных ситуациях и без потерь данных
Ух… Довольно длинный пункт. Давайте я буду дальше сокращать его до «ограниченное неявное преобразование» Так что же значит однозначная ситуация и потери данных?
Однозначная ситуация, это преобразование или операция в которой сущность сразу понятна. Вот например сложение двух чисел — однозначная ситуация. А преобразование числа в массив — нет (возможно создастся массив из одного элемента, возможно массив, с такой длинной, заполненный элементами по-умолчанию, а возможно число преобразуется в строку, а затем в массив символов).
Потеря данных это еще проще. Если мы преобразуем вещественное число 3.5 в целое — мы потеряем часть данных (на самом деле эта операция еще и неоднозначная — как будет производиться округление? В большую сторону? В меньшую? Отбрасывание дробной части?).
Преобразования в неоднозначных ситуациях и преобразования с потерей данных — это очень, очень плохо. Ничего хуже этого в программировании нет.
Если вы мне не верите, изучите язык PL/I или даже просто поищите его спецификацию. В нем есть правила преобразования между ВСЕМИ типами данных! Это просто ад!
Ладно, давайте вспомним про ограниченное неявное преобразование. Есть ли такие языки? Да, например в Pascal Вы можете преобразовать целое число в вещественное, но не наоборот. Также похожие механизмы есть в C#, Groovy и Common Lisp.
Ладно, я говорил, что есть еще способ получить пару плюсов слабой типизации в сильном языке. И да, он есть и называется полиморфизм конструкторов.
Я поясню его на примере замечательного языка Haskell.
Полиморфные конструкторы появились в результате наблюдения, что чаще всего безопасные неявные преобразования нужны при использовании числовых литералов.
И это сделано в Haskell, благодаря тому, что у литерала 1 нет конкретного типа. Это ни целое, ни вещественное, ни комплексное. Это же просто число!
Конечно спасает этот прием только при использовании смешанных выражений с числовыми литералами, а это лишь верхушка айсберга.
Таким образом можно сказать, что лучшим выходом будет балансирование на грани, между сильной и слабой типизацией. Но пока идеальный баланс не держит ни один язык, поэтому я больше склоняюсь к сильно типизированным языкам (таким как Haskell, Java, C#, Python), а не к слабо типизированным (таким как C, JavaScript, Lua, PHP).
Ладно, пойдем дальше?
Явная и неявная типизации
Язык с явной типизацией предполагает, что программист должен указывать типы всех переменных и функций, которые объявляет. Английский термин для этого — explicit typing.
Язык с неявной типизацией, напротив, предлагает Вам забыть о типах и переложить задачу вывода типов на компилятор или интерпретатор. Английски термин для этого — implicit typing.
По-началу можно решить, что неявная типизация равносильна динамической, а явная — статической, но дальше мы увидим, что это не так.
Есть ли плюсы у каждого вида, и опять же, есть ли их комбинации и есть ли языки с поддержкой обоих методов?
Преимущества явной типизации
Преимущества неявной типизации
Явная типизация по-выбору
Есть языки, с неявной типизацией по-умолчанию и возможностью указать тип значений при необходимости. Настоящий тип выражения транслятор выведет автоматически. Один из таких языков — Haskell, давайте я приведу простой пример, для наглядности:
* Спасибо int_index за нахождение ошибки.
Хм. Как мы видим, это очень красиво и коротко. Запись функции занимает всего 18 символов на одной строчке, включая пробелы!
Однако автоматический вывод типов довольно сложная вещь, и даже в таком крутом языке как Haskell, он иногда не справляется. (как пример можно привести ограничение мономорфизма)
Есть ли языки с явной типизацией по-умолчанию и неявной по-необходимости? Кон
ечно.
Неявная типизация по-выбору
В новом стандарте языка C++, названном C++11 (ранее назывался C++0x), было введено ключевое слово auto, благодаря которому можно заставить компилятор вывести тип, исходя из контекста:
Неплохо. Но запись сократилась не сильно. Давайте посмотрим пример с итераторами (если не понимаете, не бойтесь, главное заметьте, что запись благодаря автоматическому выводу очень сильно сокращается):
Ух ты! Вот это сокращение. Ладно, но можно ли сделать что-нибудь в духе Haskell, где тип возвращаемого значения будет зависеть от типов аргументов?
И опять ответ да, благодаря ключевому слову decltype в комбинации с auto:
Может показаться, что эта форма записи не сильно хороша, но в комбинации с обобщенным программированием (templates / generics) неявная типизация или автоматический вывод типов творят чудеса.
Некоторые языки программирования по данной классификации
Я приведу небольшой список из популярных языков и напишу как они подразделяются по каждой категории “типизаций”.
Возможно я где-то ошибся, особенно с CL, PHP и Obj-C, если по какому-то языку у Вас другое мнение — напишите в комментариях.
Заключение
Окей. Уже скоро будет светло и я чувствую, что про типизацию больше нечего сказать. Ой как? Тема бездонная? Очень много осталось недосказано? Прошу в комментарии, поделитесь полезной информацией.
Всё, что вы хотели знать о динамическом программировании, но боялись спросить
Я был крайне удивлён, найдя мало статей про динамическое программирование (далее просто динамика) на хабре. Мне всегда казалось, что эта парадигма довольно сильно распространена, в том числе и за пределами олимпиад по программированию. Поэтому я постараюсь закрыть этот пробел своей статьёй.
Основы
Пожалуй, лучшее описание динамики в одно предложение, которое я когда либо слышал:
Динамическое программирование — это когда у нас есть задача, которую непонятно как решать, и мы разбиваем ее на меньшие задачи, которые тоже непонятно как решать. (с) А. Кумок.
Чтобы успешно решить задачу динамикой нужно:
1) Состояние динамики: параметр(ы), однозначно задающие подзадачу.
2) Значения начальных состояний.
3) Переходы между состояниями: формула пересчёта.
4) Порядок пересчёта.
5) Положение ответа на задачу: иногда это сумма или, например, максимум из значений нескольких состояний.
Порядок пересчёта
Существует три порядка пересчёта:
1) Прямой порядок:
Состояния последовательно пересчитывается исходя из уже посчитанных.
2) Обратный порядок:
Обновляются все состояния, зависящие от текущего состояния.
3) Ленивая динамика:
Рекурсивная мемоизированная функция пересчёта динамики. Это что-то вроде поиска в глубину по ацикличному графу состояний, где рёбра — это зависимости между ними.
Элементарный пример: числа Фибоначчи. Состояние — номер числа.
Все три варианта имеют права на жизнь. Каждый из них имеет свою область применения, хотя часто пересекающуюся с другими.
Многомерная динамика
Пример одномерной динамики приведён выше, в «порядке пересчёта», так что я сразу начну с многомерной. Она отличается от одномерной, как вы уже наверно догадались, количеством измерений, то есть количеством параметров в состоянии. Классификация по этому признаку обычно строится по схеме «один-два-много» и не особо принципиальна, на самом деле.
Многомерная динамика не сильно отличается от одномерной, в чём вы можете убедиться взглянув на пару примеров:
Пример №1: Количество СМСок
Раньше, когда у телефонов были кнопки, их клавиатуры выглядели примерно так:
Требуется подсчитать, сколько различных текстовых сообщений множно написать используя не более k нажатий на такой клавиатуре.
Прямой пересчёт:
Обратный пересчёт:
При использовании обратного пересчёта всё проще: мы всегда обращаемся вперёд, так что в отрицательные элементы мы не уйдём.
5) Ответ — это сумма всех состояний.
Пример №2: Конь
4) А теперь самое интересное в этой задаче: порядок. Здесь нельзя просто взять и пройтись по строкам или по столбцам. Потому что иначе мы будем обращаться к ещё не пересчитанным состояниям при прямом порядке, и будем брать ещё недоделанные состояния при обратном подходе.
Есть два пути:
1) Придумать хороший обход.
2) Запустить ленивую динамику, пусть сама разберётся.
Если лень думать — запускаем ленивую динамику, она отлично справится с задачей.
Если не лень, то можно придумать обход наподобие такого:
Этот порядок гарантирует обработанность всех требуемых на каждом шаге клеток при прямом обходе, и обработанность текущего состояния при обратном.
Динамика и матрица переходов
Если никогда не умножали матрицы, но хотите понять этот заголовок, то стоит прочитать хотя бы вики.
А теперь, зачем всё это надо. Умножение матриц обладает свойством ассоциативности, то есть 

А теперь пример посерьёзнее:
Пример №3: Пилообразная последовательность
Для начала решение без матрицы перехода:
Динамика по подотрезкам
Это класс динамики, в котором состояние — это границы подотрезка какого-нибудь массива. Суть в том, чтобы подсчитать ответы для подзадач, основывающихся на всех возможных подотрезках нашего массива. Обычно перебираются они в порядке увеличения длины, и пересчёт основывается, соответственно на более коротких отрезках.
Пример №4: Запаковка строки
Вот Развернутое условие. Я вкратце его перескажу:
Необходимо по строке s узнать длину самой короткой сжатой строки, разжимающийся в неё.
Решается эта задача, как вы уже наверняка догадались, динамикой по подотрезкам.
1) Состояние динамики: d[l][r] — сжатая строка минимальной длины, разжимающаяся в строку s[l:r]
2) Начальные состояния: все подстроки длины один можно сжать только в них самих.
3) Пересчёт динамики:
У лучшего ответа есть какая-то последняя операция сжатия: либо это просто строка из заглавных букв, или это конкатенация двух строк, или само сжатие. Так давайте переберём все варианты и выберем лучший.
Пример №5: Дубы
Динамика по поддеревьям
Параметром состояния динамики по поддеревьям обычно бывает вершина, обозначающая поддерево, в котором эта вершина — корень. Для получения значения текущего состояния обычно нужно знать результаты всех своих детей. Чаще всего реализуют лениво — просто пишут поиск в глубину из корня дерева.
Пример №6: Логическое дерево
Требуется найти минимальное количество изменений логических операций во внутренних вершинах, такое, чтобы изменилось значение в корне или сообщить, что это невозможно.
Динамика по подмножествам
В динамике по подмножествам обычно в состояние входит маска заданного множества. Перебираются чаще всего в порядке увеличения количества единиц в этой маске и пересчитываются, соответственно, из состояний, меньших по включению. Обычно используется ленивая динамика, чтобы специально не думать о порядке обхода, который иногда бывает не совсем тривиальным.
Пример №7: Гамильтонов цикл минимального веса, или задача коммивояжера
Динамика по профилю
Классическими задачами, решающимися динамикой по профилю, являются задачи на замощение поля какими-нибудь фигурами. Причём спрашиваться могут разные вещи, например, количество способов замощения или замощение минимальным количеством фигур.
Профиль — это k (зачастую один) столбцов, являющиеся границей между уже замощённой частью и ещё не замощённой. Эта граница заполнена только частично. Очень часто является частью состояния динамики.
Почти всегда состояние — это профиль и то, где этот профиль. А переход увеличивает это местоположение на один. Узнать, можно ли перейти из одного профиля в другой можно за линейное от размера профиля время. Это можно проверять каждый раз во время пересчёта, но можно и предподсчитать. Предподсчитывать будем двумерный массив can[mask][next_mask] — можно ли от одной маски перейти к другой, положив несколько фигурок, увеличив положение профиля на один. Если предподсчитывать, то времени на выполнение потребуется меньше, а памяти — больше.
Пример №8: Замощение доминошками
Здесь профиль — это один столбец. Хранить его удобно в виде двоичной маски: 0 — не замощенная клетка столбца, 1 — замощенная. То есть всего профилей 
0) Предподсчёт (опционально): перебрать все пары профилей и проверить, что из одного можно перейти в другой. В этой задаче это проверяется так:
Примеры переходов (из верхнего профиля можно перейти в нижние и только в них):
Полученная асимптотика — 
Динамика по изломанному профилю
Это очень сильная оптимизация динамики по профилю. Здесь профиль — это не только маска, но ещё и место излома. Выглядит это так:
Теперь, после добавления излома в профиль, можно переходить к следующему состоянию, добавляя всего одну фигурку, накрывающую левую клетку излома. То есть увеличением числа состояний в N раз (надо помнить, где место излома) мы сократили число переходов из одного состояния в другое с 


Переходы в динамике по изломанному профилю на примере задачи про замощение доминошками (пример №8):
Восстановление ответа
Иногда бывает, что просто знать какую-то характеристику лучшего ответа недостаточно. Например, в задаче «Запаковка строки» (пример №4) мы в итоге получаем только длину самой короткой сжатой строки, но, скорее всего, нам нужна не её длина, а сама строка. В таком случае надо восстановить ответ.
В каждой задаче свой способ восстановления ответа, но самые распространенные:
Небольшие оптимизации
Память
Зачастую в динамике можно встретить задачу, в которой состояние требует быть посчитанными не очень большое количество других состояний. Например, при подсчёте чисел Фибоначчи мы используем только два последних, а к предыдущим уже никогда не обратимся. Значит, можно про них забыть, то есть не хранить в памяти. Иногда это улучшает асимптотическую оценку по памяти. Этим приёмом можно воспользоваться в примерах №1, №2, №3 (в решении без матрицы перехода), №7 и №8. Правда, этим никак не получится воспользоваться, если порядок обхода — ленивая динамика.
Время
Иногда бывает так, что можно улучшить асимптотическое время, используя какую-нибудь структуру данных. К примеру, в алгоритме Дейкстры можно воспользоваться очередью с приоритетами для изменения асимптотического времени.
Замена состояния
В решениях динамикой обязательно фигурирует состояние — параметры, однозначно задающие подзадачу, но это состояние не обязательно одно единственное. Иногда можно придумать другие параметры и получить с этого выгоду в виде снижения асимптотического времени или памяти.
Пример №9: Разложение числа
Решение №1:
Решение №2:

Строки здесь обозначают слагаемые.
Первое решение последовательно добавляет по одной строчке внизу таблицы, а второе — по одному столбцу слева таблицы. Вариантов размера следующей строчки много — главное, чтобы она была больше предыдущей, а столбцов — только два: такой же как предыдущий и на единичку больше.
Заключение
Основным источником была голова, а туда информация попала с лекций в Летней Компьютерной Школе (для школьников), а также кружка Андрея Станкевича и спецкурса Михаила Дворкина (darnley).
Спасибо за внимание, надеюсь эта статья кому-нибудь пригодится! Хотя мне уже пригодилась — оказывается, написание статьи это хороший способ всё вспомнить.