форма свободных колебаний системы совершающихся по гармоническому закону с одной и той же частотой

Строительная механика (стр. 6 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6

174 Статический метод

D Statische Methode

F Methode statique

Метод определения критической на­грузки из условия равновесия системы в отклоненном состоянии.

175 Энергетический метод

D Energetische Methode

E Strain energy method

F Methode basee sur 1’energy de deformation

Метод определения критической нагруз­ки из условия равенства нулю прира­щения полной энергии системы при пе­реходе ее в смежное состояние.

176 Динамический метод

D Dynamische Methode

F Methode dynamique

Метод определения критической на­грузки, основанный на рассмотрении ко­лебаний систем.

177 Качественные методы

Методы исследования устойчивости, ос­нованные на качественном анализе вы­ражений энергии и уравнений равнове­сия или движения системы.

178 Степень свободы

Е Degree of freedom

F Degre de la mobilite

Кинематическая характеристика систе­мы, представляющая наименьшее число независимых параметров, с помощью которых можно определить положение всех точек системы в любой момент времени.

D Selbsterregte Schwingungen

E Self-excited vibrations

F Vibrations autexcitees

Незатухающие периодические колеба­ния системы, характеризующиеся на­личием постоянного непериодического источника энергии и обратной связи, регулирующей поступление энергии из источника.

180 Параметрические колебания

D Quasiharmonische Schwin­gungen

E Vibration of system with variable charac-teristics

F Vibrations des systemes a caracteristiques elasti-ques variables

Колебания, связанные с периодическими изменениями параметров системы, на­пример ее жесткости.

181 Коэффициент затухания

E Damping coefficient

F Coefficient d’amortisse-ment

Отношение двух последовательных (од­ного знака) амплитуд при затухающих свободных колебаниях.

182 Логарифмический декремент колебаний

E Damping decrement

F Decrement d’amortisse-ment

Натуральный логарифм коэффициента затухания.

183 Устойчивость колебаний

Способность динамической системы вос­станавливать установившиеся колеба­ния при малых возмущениях.

184 Ударная нагрузка

F Forces de percussion

Кратковременная динамическая на­грузка, возникающая при ударении тел конечной массы о сооружение.

185 Кратковременная нагрузка

Нрк Импульсивная нагрузка

Динамическая нагрузка, продолжитель­ность действия которой мала по сравне­нию с периодом основного тона соб­ственных колебаний системы.

186 Критическая скорость движе­ния нагрузки

D Kritische Geschwindigkeit

F Vitesse critique

Скорость движения нагрузки по кон­струкции, при которой динамические перемещения или внутренние усилия до­стигают предельных значений.

187 Свободные колебания

D Freie Schwingungen

F Vibrations libres. Vibrations propres

Колебания систем, вызванные началь­ным возмущением.

188 Вынужденные колебания

D Erzwungene Schwingungen

E Forced vibrations. Const-rained vibrations

F Vibrations forcиes

Колебания систем, вызванные действием переменных во времени нагрузок.

189 Собственная форма колебаний

Форма собственных колебаний

E Mode of normal vibrations

Форма свободных колебаний системы, совершающихся по гармоническому закону с одной и той же частотой.

190 Собственные колебания

E Normal vibrations

F Vibrations propres

Свободные колебания по одной из собственных форм.

191 Частота собственных колебаний

E Frequency of normal vibrations

F Frиquence des vibrations propres

Число собственных колебаний в секунду.

192 Спектр собственных частот

E Normal frequency spectrum

Совокупность собственных частот системы, расположенных в порядке их возрастания.

193 Круговая частота колебаний

E Angular frequency

Число колебаний в 2р сек.

Источник

Расчет на устойчивость

D Statische Methode

F Methode statique

Метод определения критической на­грузки из условия равновесия системы в отклоненном состоянии.

D Energetische Methode

E Strain energy method

F Methode basee sur 1’energy de deformation

Метод определения критической нагруз­ки из условия равенства нулю прира­щения полной энергии системы при пе­реходе ее в смежное состояние.

D Dynamische Methode

F Methode dynamique

Метод определения критической на­грузки, основанный на рассмотрении ко­лебаний систем.

177 Качественные методы

Методы исследования устойчивости, ос­нованные на качественном анализе вы­ражений энергии и уравнений равнове­сия или движения системы.

IV. Динамика

Е Degree of freedom

F Degre de la mobilite

Кинематическая характеристика систе­мы, представляющая наименьшее число независимых параметров, с помощью которых можно определить положение всех точек системы в любой момент времени.

D Selbsterregte Schwingungen

E Self-excited vibrations

F Vibrations autexcitees

Незатухающие периодические колеба­ния системы, характеризующиеся на­личием постоянного непериодического источника энергии и обратной связи, регулирующей поступление энергии из источника.

180 Параметрические колебания

D Quasiharmonische Schwin­gungen

E Vibration of system with variable charac-teristics

F Vibrations des systemes a caracteristiques elasti-ques variables

Колебания, связанные с периодическими изменениями параметров системы, на­пример ее жесткости.

E Damping coefficient

F Coefficient d’amortisse-ment

Отношение двух последовательных (од­ного знака) амплитуд при затухающих свободных колебаниях.

182 Логарифмический декремент колебаний

E Damping decrement

F Decrement d’amortisse-ment

Натуральный логарифм коэффициента затухания.

183 Устойчивость колебаний

Способность динамической системы вос­станавливать установившиеся колеба­ния при малых возмущениях.

F Forces de percussion

Кратковременная динамическая на­грузка, возникающая при ударении тел конечной массы о сооружение.

185 Кратковременная нагрузка

Нрк Импульсивная нагрузка

Динамическая нагрузка, продолжитель­ность действия которой мала по сравне­нию с периодом основного тона соб­ственных колебаний системы.

186 Критическая скорость движе­ния нагрузки

D Kritische Geschwindigkeit

F Vitesse critique

Скорость движения нагрузки по кон­струкции, при которой динамические перемещения или внутренние усилия до­стигают предельных значений.

D Freie Schwingungen

F Vibrations libres. Vibrations propres

Колебания систем, вызванные началь­ным возмущением.

188 Вынужденные колебания

E Forced vibrations. Const-rained vibrations

F Vibrations forcèes

Колебания систем, вызванные действием переменных во времени нагрузок.

189 Собственная форма колебаний

Форма собственных колебаний

E Mode of normal vibrations

Форма свободных колебаний системы, совершающихся по гармоническому закону с одной и той же частотой.

190 Собственные колебания

E Normal vibrations

F Vibrations propres

Свободные колебания по одной из собственных форм.

191 Частота собственных колебаний

E Frequency of normal vibrations

F Frèquence des vibrations propres

Число собственных колебаний в секунду.

192 Спектр собственных частот

E Normal frequency spectrum

Совокупность собственных частот системы, расположенных в порядке их возрастания.

193 Круговая частота колебаний

E Angular frequency

Число колебаний в 2π сек.

1См. Д. С. Лотте. Основы построения научно-технической терминологии. Изд-во АН СССР, 1961. Как работать над терминологией. Основы и методы. Пособие составленное по трудам Д. С. Лотте и Комитета научно-технической терминологии АН СССР. Изд-во «Наука», 1968.

Источник

Собственная форма колебаний

Собственная форма колебаний (вибрации) системы – форма колебаний (вибрации) линейной системы, колеблющейся с одной из собственных частот.

Собственная форма колебаний – форма свободных колебаний системы, совершающихся по гармоническому закону с одной и той же частотой.

[Отраслевой руководящий документ. Техническая эксплуатация железобетонных конструкций производственных зданий. Часть1.г. Москва 1993 г.]

Рубрика термина: Виды вибрации

Полезное

Смотреть что такое «Собственная форма колебаний» в других словарях:

собственная форма колебаний — форма собственных колебаний Форма свободных колебаний системы, совершающихся по гармоническому закону с одной и той же частотой. [Сборник рекомендуемых терминов. Выпуск 82. Строительная механика. Академия наук СССР. Комитет научно технической… … Справочник технического переводчика

собственная форма колебаний — собственная форма колебаний; собственная форма Форма колебаний линейной системы, колеблющейся с одной из собственных частот … Политехнический терминологический толковый словарь

собственная форма колебаний — natural mode of vibration Форма свободного гармонического колебания недемпфируемой линейной системы, колеблющейся с одной из ее собственных частот. Шифр IFToMM: 3.9.28 Раздел: КОЛЕБАНИЯ В МЕХАНИЗМАХ … Теория механизмов и машин

собственная форма колебаний (вибрации) системы — собственная форма Форма колебаний (вибрации) линейной системы, колеблющейся с одной из собственных частот. Пояснения Термины и определения для близких понятий, различающиеся лишь отдельными словами, совмещены, причем слова, которые отличают… … Справочник технического переводчика

Собственная форма колебаний (вибрации) системы — 118. Собственная форма колебаний (вибрации) системы Собственная форма Форма колебаний (вибрации) линейной системы, колеблющейся с одной из собственных частот Источник: ГОСТ 24346 80: Вибрация. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации

Собственная форма колебаний системы — 56. Собственная форма колебаний системы Форма колебаний линейной системы, колеблющейся с одной из собственных частот Источник … Словарь-справочник терминов нормативно-технической документации

собственная форма — колебаний; собственная форма Форма колебаний линейной системы, колеблющейся с одной из собственных частот … Политехнический терминологический толковый словарь

собственная мода (гибкого ротора) ф _n(z) — 3.3 собственная мода (гибкого ротора) ф n(z): Форма пространственных колебаний на одной из критических скоростей (гибкого ротора) при отсутствии демпфирования в системе «ротор опора». Источник: ГОСТ 31320 2006: Вибрация. Методы и критерии… … Словарь-справочник терминов нормативно-технической документации

Генерирование электрических колебаний — процесс преобразования различных видов электрической энергии в энергию электрических (электромагнитных) колебаний. Термин «Г. э. к.» применяется обычно к колебаниям в диапазоне радиочастот, возбуждаемым в устройствах (системах) с… … Большая советская энциклопедия

Источник

Гармонические колебания

9 класс, 11 класс, ЕГЭ/ОГЭ

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение характеризуется величинами: период, частота, амплитуда, фаза колебаний.

Формула периода колебаний

T = t/N

N — количество колебаний [-]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [-]

Она используется в уравнении гармонических колебаний:

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

2πνtв этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

g — ускорение свободного падения [м/с^2]

На планете Земля g = 9,8 м/с2

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

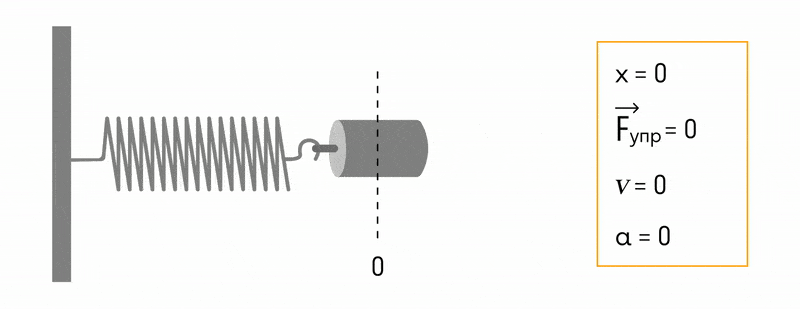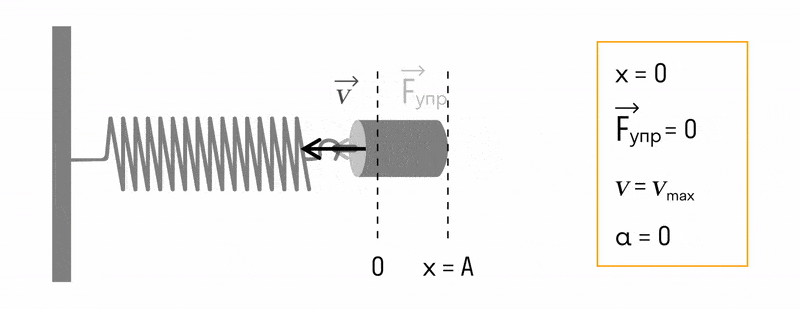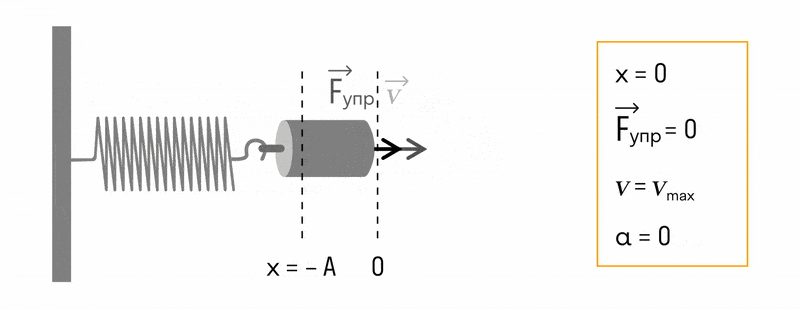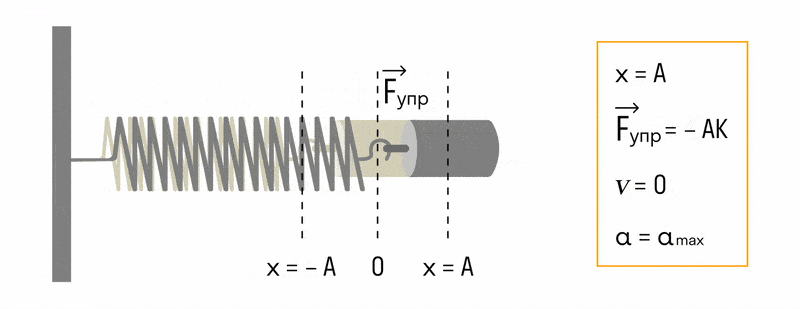
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

Рассмотрим его на примере математического маятника.

Источник

Свободные колебания

Колебания – в той или иной степени повторяющийся во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.

Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму. Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны с волнами. Поэтому исследованиями этих закономерностей занимается обобщенная теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии.

Свободные колебания – колебания в системе под действием внутренних тел, после того как система выведена из положения равновесия. Колебания груза, подвешенного на нити, или груза, прикрепленного к пружине, – это примеры свободных колебаний. После выведения этих систем из положения равновесия создаются условия, при которых тела колеблются без воздействия внешних сил. Система – группа тел, движение которых мы изучаем. Внутренние силы – силы, действующие между телами системы. Внешние силы – силы, действующие на тела системы со стороны тел, не входящих в нее.

Условия возникновения свободных колебаний.

Для того чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

В этом соотношении \(\omega\) – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими.

Таким образом, груз некоторой массы m, прикрепленный к пружине с жесткостью k, второй конец которой закреплен неподвижно, составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором.

Круговая частота ω₀ свободных колебаний груза на пружине находится из второго закона Ньютона:

Частота ω₀ называется собственной частотой колебательной системы.

Период T гармонических колебаний груза на пружине равен

и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты \(ω_0\) и периода колебаний T справедливы и в этом случае.

Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела a и координатой x: ускорение является второй производной координаты тела x по времени t:

Поэтому второй закон Ньютона для груза на пружине может быть записан в виде

Все физические системы (не только механические), описываемые уравнением (·), способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида

Уравнение (·) называется уравнением свободных колебаний. Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний \(ω_0\) или период T. Такие параметры колебательного процесса, как амплитуда \(x_m\) и начальная фаза φ₀, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени.

Если же грузу, находившемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость \(\pm v_0,\) то \(x_m=\sqrt<\frac mk>v_0,\varphi_0=\pm\frac \pi2.\)

Таким образом, амплитуда \(x_m\) свободных колебаний и его начальная фаза \(φ_0\) определяются начальными условиями.

Пе­ри­од ко­ле­ба­ний по­тен­ци­аль­ной энер­гии пру­жин­но­го ма­ят­ни­ка равен \(1\) с. Каким будет пе­ри­од ее ко­ле­ба­ний, если массу груза ма­ят­ни­ка и жест­кость пру­жи­ны уве­ли­чить в \(4\) раза?

Пе­ри­од ко­ле­ба­ний по­тен­ци­аль­ной энер­гии го­ри­зон­таль­но­го пру­жин­но­го ма­ят­ни­ка – \(1\) с. Каким будет пе­ри­од ее ко­ле­ба­ний, если массу груза ма­ят­ни­ка уве­ли­чить в \(2\) раза, а жест­кость пру­жи­ны вдвое умень­шить?

Гиря массой \(2\) кг подвешена на пружине жесткостью \(50\) Н/м. Период свободных колебаний груза

После отклонения от положения равновесия на \(1\) см математический маятник совершает свободные колебания с периодом в \(1\) с. При отклонении от положения равновесия на \(2\) см тот же маятник будет совершать колебания с периодом

Тело совершает \(120\) колебаний за \(2\) мин. Чему равны период и частота этих колебаний?

Как изменится период свободных колебаний маятника длиной \(10\) м, если амплитуды его колебаний увеличить от \(10\) см до \(20\) см?

Материальная точка совершает гармонические колебания по закону \(x = 0,07 \cdot \cos\big( πt + \frac<π> <2>\big)\) в единицах СИ. Определите амплитуду колебаний.

Найдите массу груза, который на пружине с жесткостью \(250\) Н/м за \(3,14\) с совершает \(5\) колебаний.

Периоды колебаний двух математических маятников относятся как 3:2. Первый маятник длиннее второго в

Шарик, подвешенный на пружине, за \( \frac<1><6>\) периода сместился от крайнего положения на \(15\) см. Определите амплитуду колебаний.

У математического маятника длиной \(250\) см период колебаний равен ( \(g\approx10\) м/с \(^2\) )

Шарик колеблется на пружине жесткостью \(0,25\) кН/м, при этом за \(16\) с совершает \(20\) колебаний. Определите его массу.

На графике показана зависимость смещения груза, совершающего колебания на пружинном маятнике, от времени. Жесткость пружины – \(0,1\) кН/м. Чему равна масса этого груза?

Чему равна циклическая частота колебаний груза массой \(18·10^3\) г, закрепленного на пружине жесткостью \(200\) Н/м?

Астронавт взял с собой на Луну математический маятник, который на Земле имел период колебаний \(2\) с. Изменится ли этот период колебаний на Луне?

В пруду на поверхности воды качается бумажный кораблик, длина волны – \(2,\!5\) м и она распространяется со скоростью \(120\) см/с. Определите период и частоту колебаний бумажного кораблика.

Амплитуда колебаний математического маятника равна \(8\) см, наибольшая скорость тела – \(0,2\) м/с. Чему равна длина этого маятника?

Чему равна частота колебаний груза массой \(40\) г на пружине жесткостью \(100\) Н/м?

Как изменится частота колебаний математического маятника, если его длину уменьшить в \(4\) раза?

Чему равна скорость волн, распространяющихся в озере, если поплавок совершает \(6\) колебаний за \(15\) секунд и расстояние между соседними горбами волны равно \(60\) см?

С какой частотой будет совершать колебания груз массой \(100\) г на пружине жесткостью \(40\) Н/м?

Чему равна длина математического маятника, если он совершает \(20\) колебаний за \(5\) с? ( \(g\approx10\) м/с \(^2\) )

Тело массой \(300\) г подвесили сначала на нити длиной \(1,5\) м, затем на пружине для совершения колебаний. При этом период колебаний в том и другом случае оказался одинаковым. Чему была равна жесткость пружины? ( \(g\approx10\) м/с \(^2\) )

Источник

Не пропустите наши новые статьи:

ярмольник ведущий каких программ

Ярлыки не работают что делать если ярлыки не открываются как восстановить ярлыки программы

Ярлык стал белым что делать windows 10

японская система развития интеллекта и памяти программа 60 дней читать

японская система развития интеллекта и памяти программа 60 дней питер

wpDiscuz