Калькулятор расчета кредита в Excel и формулы ежемесячных платежей
Excel – это универсальный аналитическо-вычислительный инструмент, который часто используют кредиторы (банки, инвесторы и т.п.) и заемщики (предприниматели, компании, частные лица и т.д.).
Быстро сориентироваться в мудреных формулах, рассчитать проценты, суммы выплат, переплату позволяют функции программы Microsoft Excel.
Как рассчитать платежи по кредиту в Excel
Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:
Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.
Расчет аннуитетных платежей по кредиту в Excel
Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:
Формула коэффициента аннуитета:
В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:
Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.
Расчет платежей в Excel по дифференцированной схеме погашения
Дифференцированный способ оплаты предполагает, что:
Формула расчета дифференцированного платежа:
ДП = ОСЗ / (ПП + ОСЗ * ПС)
Составим график погашения предыдущего кредита по дифференцированной схеме.
Входные данные те же:
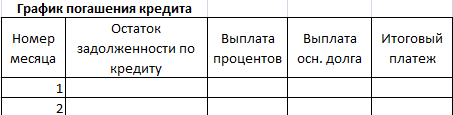
Составим график погашения займа:
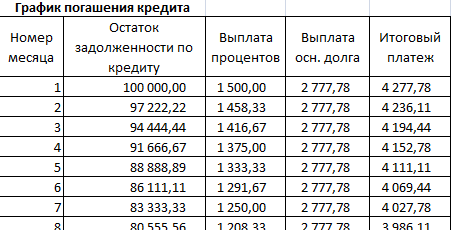
Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.
Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).
Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9 Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.
Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.
Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:
Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.
Формула расчета процентов по кредиту в Excel
Проведем расчет процентов по кредиту в Excel и вычислим эффективную процентную ставку, имея следующую информацию по предлагаемому банком кредиту:
Рассчитаем ежемесячную процентную ставку и платежи по кредиту:
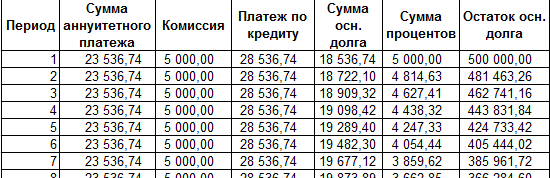
Заполним таблицу вида:
Комиссия берется ежемесячно со всей суммы. Общий платеж по кредиту – это аннуитетный платеж плюс комиссия. Сумма основного долга и сумма процентов – составляющие части аннуитетного платежа.
Сумма основного долга = аннуитетный платеж – проценты.
Сумма процентов = остаток долга * месячную процентную ставку.
Остаток основного долга = остаток предыдущего периода – сумму основного долга в предыдущем периоде.
Опираясь на таблицу ежемесячных платежей, рассчитаем эффективную процентную ставку:
Эффективная процентная ставка кредита без комиссии составит 13%. Подсчет ведется по той же схеме.
Расчет полной стоимости кредита в Excel
Согласно Закону о потребительском кредите для расчета полной стоимости кредита (ПСК) теперь применяется новая формула. ПСК определяется в процентах с точностью до третьего знака после запятой по следующей формуле:
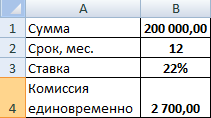
Возьмем для примера следующие данные по кредиту:
Для расчета полной стоимости кредита нужно составить график платежей (порядок см. выше).
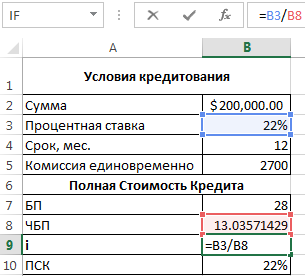
Нужно определить базовый период (БП). В законе сказано, что это стандартный временной интервал, который встречается в графике погашения чаще всего. В примере БП = 28 дней.
Далее находим ЧБП: 365 / 28 = 13.
Теперь можно найти процентную ставку базового периода:
У нас имеются все необходимые данные – подставляем их в формулу ПСК: =B9*B8
Примечание. Чтобы получить проценты в Excel, не нужно умножать на 100. Достаточно выставить для ячейки с результатом процентный формат.
ПСК по новой формуле совпала с годовой процентной ставкой по кредиту.
Таким образом, для расчета аннуитетных платежей по кредиту используется простейшая функция ПЛТ. Как видите, дифференцированный способ погашения несколько сложнее.
Расчет кредита в Excel
Так что очень надеюсь, что изложенный ниже материал вам не пригодится.
Но если уж случится так, что вам или вашим близким придется влезть в это дело, то неплохо бы перед походом в банк хотя бы ориентировочно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. «Помассажировать числа» заранее, как я это называю 
Вариант 1. Простой кредитный калькулятор в Excel
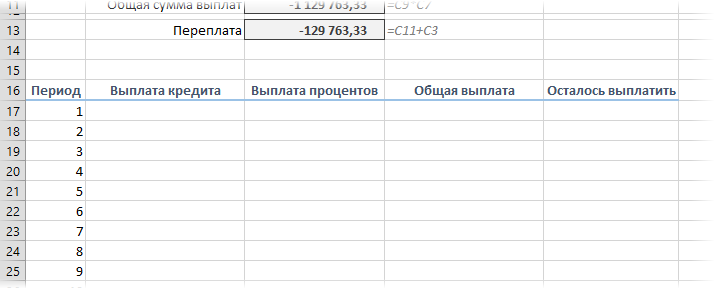
Также полезно будет прикинуть общий объем выплат и переплату, т.е. ту сумму, которую мы отдаем банку за временно использование его денег. Это можно сделать с помощью простых формул:
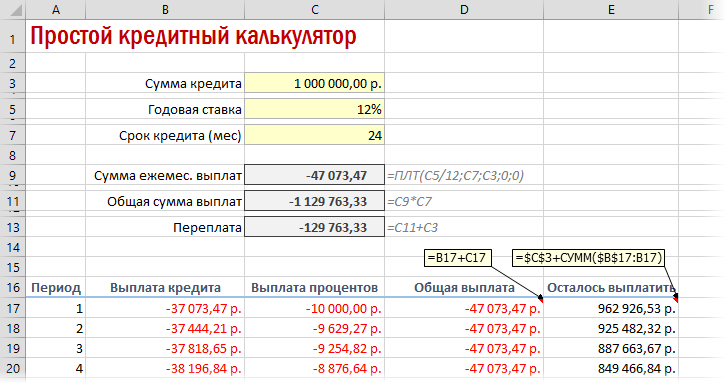
Вариант 2. Добавляем детализацию
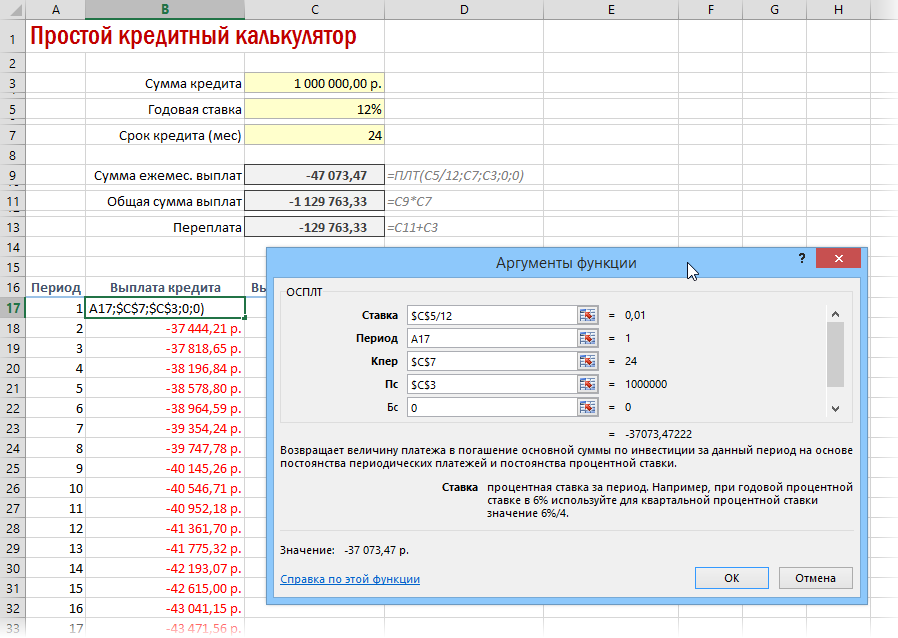
Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в предыдущем примере:
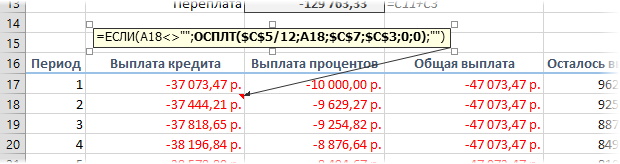
Чтобы сделать наш калькулятор более универсальным и способным автоматически подстраиваться под любой срок кредита, имеет смысл немного подправить формулы. В ячейке А18 лучше использовать формулу вида:
Эта формула проверяет с помощью функции ЕСЛИ (IF) достигли мы последнего периода или нет, и выводит пустую текстовую строку («») в том случае, если достигли, либо номер следующего периода. При копировании такой формулы вниз на большое количество строк мы получим номера периодов как раз до нужного предела (срока кредита). В остальных ячейках этой строки можно использовать похожую конструкцию с проверкой на присутствие номера периода:
=ЕСЛИ(A18<>«»; текущая формула; «»)
Т.е. если номер периода не пустой, то мы вычисляем сумму выплат с помощью наших формул с ПРПЛТ и ОСПЛТ. Если же номера нет, то выводим пустую текстовую строку:
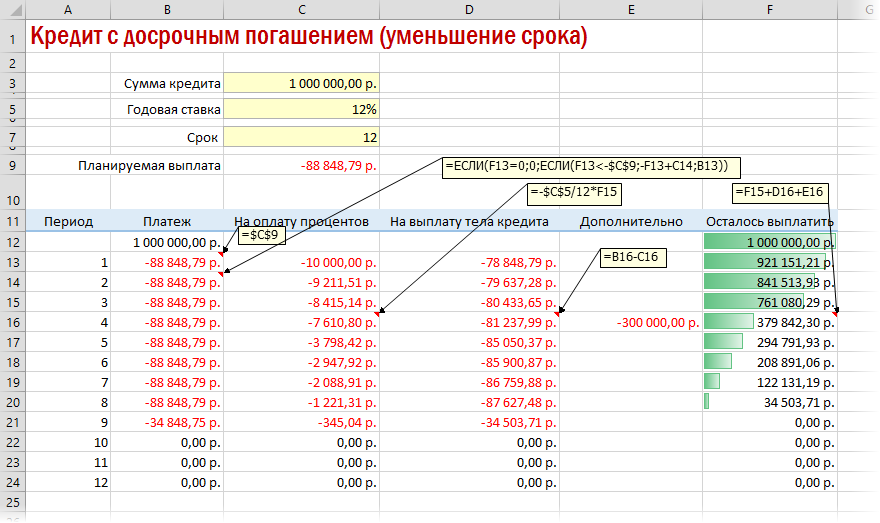
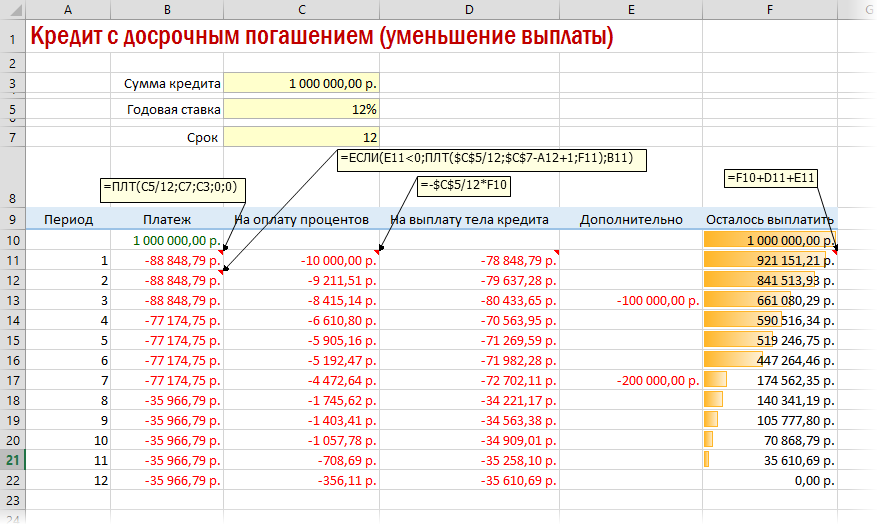
Вариант 3. Досрочное погашение с уменьшением срока или выплаты
Реализованный в предыдущем варианте калькулятор неплох, но не учитывает один важный момент: в реальной жизни вы, скорее всего, будете вносить дополнительные платежи для досрочного погашения при удобной возможности. Для реализации этого можно добавить в нашу модель столбец с дополнительными выплатами, которые будут уменьшать остаток. Однако, большинство банков в подобных случаях предлагают на выбор: сокращать либо сумму ежемесячной выплаты, либо срок. Каждый такой сценарий для наглядности лучше посчитать отдельно.
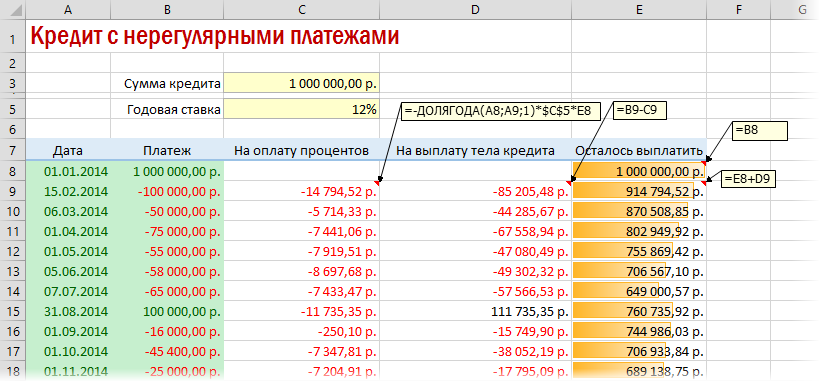
Вариант 4. Кредитный калькулятор с нерегулярными выплатами
Существуют варианты кредитов, где клиент может платить нерегулярно, в любые произвольные даты внося любые имеющиеся суммы. Процентная ставка по таким кредитам обычно выше, но свободы выходит больше. Можно даже взять в банке еще денег в дополнение к имеющемуся кредиту. Для расчета по такой модели придется рассчитывать проценты и остаток с точностью не до месяца, а до дня:
Расчет платежей
Мы разработали простой и удобный онлайн-калькулятор, с помощью которого можно сделать расчет ежемесячного платежа и суммы переплаты по потребительскому кредиту.
Рассчитать ежемесячный платеж
Виды расчета суммы кредита по ежемесячному платежу
Кредитные организации предлагают два вида расчета погашения задолженности:
Каждая из них имеет собственные особенности, достоинства, и недостатки.
Аннуитетная схема расчетов
Аннуитетный способ (или погашение равными суммами) означает, что в течение всего времени пользования кредитом заемщик вносит для погашения задолженности равные суммы за каждый период (как правило, месяц).
Главная особенность такой методики заключается в том, что обязательно погашается полная сумма процентов, которая начисляется в текущем периоде, а остаток регулярного взноса направляется на погашение части тела кредита (основной суммы задолженности). Величины и соотношение процентных выплат и средств на уменьшение основного долга изменяются в каждом периоде.
Основные понятия дифференцированного платежа
Этот вариант обслуживания кредита иначе называют погашением равными долями. При расчетах с использованием дифференцированного платежа, величина регулярных взносов также включает две составляющие:
Сравнение методов расчета
Заемщики, которые проводят сравнительные расчеты для обеих схем погашения, имеют основания утверждать, что дифференцированный платеж выгоднее аннуитетного. К примеру, для ипотечного кредита на сумму 6 миллионов рублей под 12% годовых со сроком кредитования 20 лет при дифференцированной методике расчета переплата составит 7230 тыс. рублей. Аннуитетная схема (погашение равными суммами) дает в результате сумму процентов (стоимость кредита) 9856 тыс. рублей. Особенно существенно проявляются отличия при долгосрочном кредитовании (например, в ипотечных кредитах на сроки более 10 лет).
Из других достоинств дифференцированного платежа принято выделять:
Важно! Аннуитетный платеж отлично подойдет не только для погашения наличными, но и для использования таких распространенных видов банковских услуг, как регулярные (в автоматическом режиме) платежи в счет оплаты долга с карт и/или счетов.
Основное различие между схемами состоит в определении суммы ежемесячного платежа.
При аннуитетной схеме она остается неизменной. Однако при погашении равными суммами в первые месяцы основную часть выплат составляют проценты. Остаток основной задолженности в это время уменьшается медленно, в результате чего и составляющая, идущая на процентные выплаты, остается весьма значительной.
Для заемщика, долг которого обслуживается по дифференцированной схеме, характерна другая проблема. Поскольку в состав регулярного взноса входит вся сумма начисленных за период процентов, его размер на первоначальном этапе (когда остаток тела велик) и в конце срока могут различаться весьма существенно. Так, для приведенного выше примера ипотечного кредита, сумма погашения основного долга составляет 25 тыс. руб. ежемесячно. При этом, за первый месяц пользования кредитом клиент должен перечислить банку 85 тыс.руб. (из них 60 000 – проценты по кредиту), а за последний – 25 250 рублей (2 250 рублей процентов). Такая неравномерность приводит и к усложнению долговременного планирования бюджета.
Эти отличия следует учитывать при рассмотрении других связанных с кредитованием вопросов:
Важно! Рассматривать отличие между схемами кредитования следует и в том случае, если заемщик хочет получить имущественные налоговые вычеты, например, при покупке жилья в ипотеку. В этом случае аннуитетная схема обслуживания долга даст лучшие результаты, поскольку на начальном этапе сумма процентных выплат, а, следовательно, и возврат налогов, максимальны.
Сегодня заемщику нет необходимости рассчитывать выплаты по кредиту вручную. Решить эту задачу онлайн поможет кредитный калькулятор.
Онлайн расчет платежей по кредиту на кредитном калькуляторе
Такой калькулятор предоставляют как специализированные порталы, например, banki.ru или calculator-credit.ru, так и официальные сайты кредитных организаций.
Расчет производится на основании следующих данных :
В результате расчета приведенного выше примера ипотечного кредита ориентировочные суммы по ежемесячному погашению аннуитетными платежами составляют 66 065 рублей, а общая стоимость пользования займом (сумма переплат) 9 855 640 рублей.
Более точные результаты можно получить, если воспользоваться кредитными калькуляторами банков. Они работают по тому же принципу, однако приводятся с учетом специфики условий кредитования и конкретных программ, предлагаемых финансовыми организациями.
Большинство из них позволяет учесть различные льготы для заемщиков, например, при расчете ипотеки с государственной поддержкой или пониженные кредитные ставки для клиентов-участников зарплатных проектов. Кроме того, такие калькуляторы, как правило, более функциональны, поскольку позволяют вести расчет по различным наборам исходных данных – сумме кредитования, стоимости покупки и первоначальному взносу, величине подтвержденного дохода, сроку кредитования. Практически все банковские сервисы учитывают и требования к финансовому состоянию заемщика, прежде всего, сумме доходов, в которой кредитный платеж не должен превышать 40-50%. Результатом расчета также являются параметры обслуживания кредита:
В зависимости от используемого набора входных значений определяются также необходимые суммы подтвержденного дохода, максимальный размер займа, допустимый срок кредитования.
Внимание! Результаты работы кредитных калькуляторов, даже размещенных на страницах официальных сайтов банков, не являются окончательными документами! Окончательный график погашения рассчитывается (и входит в пакет документов к кредитному договору) только после оформления и получения положительного решения по кредиту. Делает такой расчет специалист банка на этапе заключения договора.
Впрочем, для того, чтобы провести расчеты выплат по кредиту не обязательно использовать интернет-сервисы. Сделать это можно и собственными силами с помощью обычного (или встроенного в ПО смартфона) калькулятора.
Расчет аннуитетных платежей по кредиту
Поскольку аннуитетная схема является более сложной для самостоятельного расчета, ее следует рассмотреть более подробно. Для проведения вычислений используются следующие исходные данные:
Общая формула расчета регулярного платежа (Пл) выглядит просто:
Здесь Кр – расчетный коэффициент (коэффициент аннуитета) для определения величины вносимых за каждый период средств. Именно он и является основной неизвестной, для которой необходим точный расчет.
Пример расчета для приведенных выше параметров ипотечного платежа.
Ежемесячный взнос в этом случае составит
Пл = 6000000 * 0.0110108 = 66064.8 (руб.)
Полученный результат точно соответствует полученному при расчетах с использованием кредитного калькулятора.
Использование таблицы Excell для расчета платежей по кредиту
Достаточно просто сделать расчеты ежемесячных кредитных платежей с использование таблиц Excell. Программа содержит множество функций для финансовых расчетов, которые обеспечивают пользователю максимум удобства при выполнении вычислений.
Для расчета аннуитетных платежей в Excell пользователю достаточно обратиться к функции ПЛТ.
Внимание! Функция доступна только при подключенной надстройке «Пакет анализа»! В MS Excell 2007, 2010 надстройка включена по умолчанию. При отсутствии имени функции в списке ее следует подключить!
Функция (формула для расчета) имеет формат: ПЛТ(ставка;кпер;пс;[бс];[тип]).
В качестве аргументов используются:
Расчет графика погашения (если необходима подробная информация о распределении средств с остатками на конец каждого периода) использует не только приведенную формулу. Определяют также:
Расчет дифференцированного платежа по кредиту
В этом случае табличный калькулятор может использовать формулу ПРОЦПЛАТ(ставка;период;кпер;пс). Схожие по названиям аргументы аналогичны используемым при расчете аннуитета. Аргумент период означает номер периода, за который выплачиваются проценты.
Важно! Функция использует методику начисления процентов на начало периода! Для корректного расчета взносов по кредиту необходимо использовать номер периода, уменьшенный на 1 (например, для расчета за первый месяц в функции использовать период, равный 0).
Алгоритм расчета графиков погашения аналогичен, использующемуся при расчете аннуитетной схемы, только погашение тела кредита остается постоянным (сумма кредитования делится на количество периодов погашения).
Расчет кредита с остаточным платежом
Такой вид широко применяется при кредитовании автомобилей. Отличается он тем, что погашается в течение активного периода не вся основная сумма задолженности, часть ее остается для погашения последним взносом (остаточный платеж). В результате значительно уменьшается сумма регулярных выплат (особенно заметно это при дифференцированном платеже).
Формула расчета для аннуитета остается неизменной, только обязательно указывается параметр бс (ОБЯЗАТЕЛЬНО со знаком противоположным величине пс). Для дифференцированного метода изменяется только величина погашения тела кредита (рассчитывается не на полную сумму, а на разность между размером займа и величиной остаточного платежа).
Особенности расчета платежа по ипотечному кредиту
Главной отличительной особенностью расчетов выплат по ипотеке является наличие обязательных страховых платежей. Наиболее распространенным способом оплаты страховки является единовременное внесение страховых взносов за счет кредитных средств, и включение этой суммы в тело кредита. Таким образом, алгоритм расчета ежемесячного погашения остается неизменным.
В случае, если страховая компания использует другие принципы расчета с клиентами, например, ежегодные или ежемесячные выплаты взносов, их в кредитном платеже учитывают как суммы регулярных комиссий.
Расчет аннуитетных платежей по кредиту в Excel
В наш век высоких технологий и автоматизации как-то неприлично вручную выполнять сложные расчёты. Хоть аннуитетные платежи рассчитать не так и трудно, но как говорит Юрий Ашер:
«Не надо напрягать свой мозг там, где это могут сделать за вас другие!»
В нашей ситуации к вам на помощь придут: компьютер и программа Microsoft Excel.
Хотим предупредить, что команда портала temabiz.com поставила перед собой цель не просто дать вам «халяву» в виде «экселевского» файла с готовыми расчетами. Нет, в этой публикации мы вас научим самостоятельно рассчитывать аннуитетные платежи, а также составлять в программе Excel графики погашения аннуитетных кредитов. Ну а для ленивых мы, конечно же, выложим готовые файлы кредитных калькуляторов.
Как рассчитать аннуитетный платеж в Excel
Те, кто читал предыдущую публикацию, наверняка ещё долго будут с ужасом вспоминать формулу аннуитетного платежа. Но сейчас вы, дорогие друзья, можете облегчённо вздохнуть, ибо все расчёты за вас сделает программа Microsoft Excel.
Мы сделаем не просто файлик с одной циферкой. Нет! Мы разработаем настоящий инструмент, с помощью которого вы сможете рассчитать аннуитетный платёж не только для себя, но и для соседа, который ставит свою машину на детской площадке; прыщавого студента, который сутками курит в вашем подъезде; тётки, которая выгуливает свою собаку прямо под вашими окнами – короче, для всех особо одарённых. Кстати, можете поставить где-нибудь возле монитора купюроприёмник и брать с этой публики деньги.
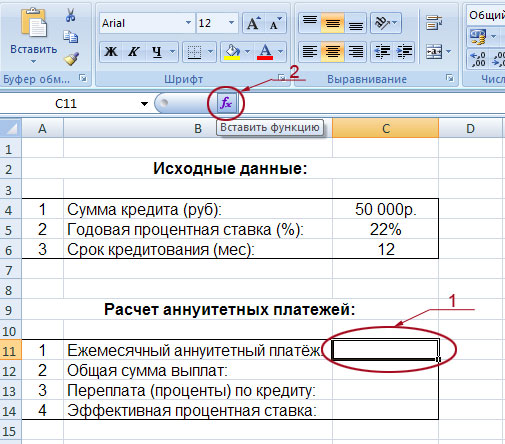
Давайте приступим к разработке нашего кредитного калькулятора. Смотрим на первый рисунок:
Итак, вы видите два блока. Один с исходными данными, а второй – с расчётами. Исходные данные (сумма кредита, годовая процентная ставка, срок кредитования) вы будете вводить вручную, а во втором блоке будут мгновенно появляться расчёты.
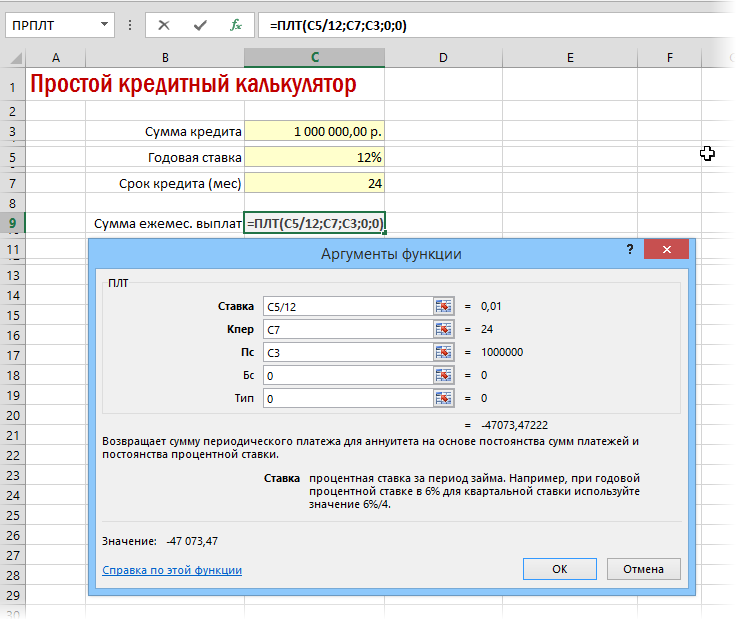
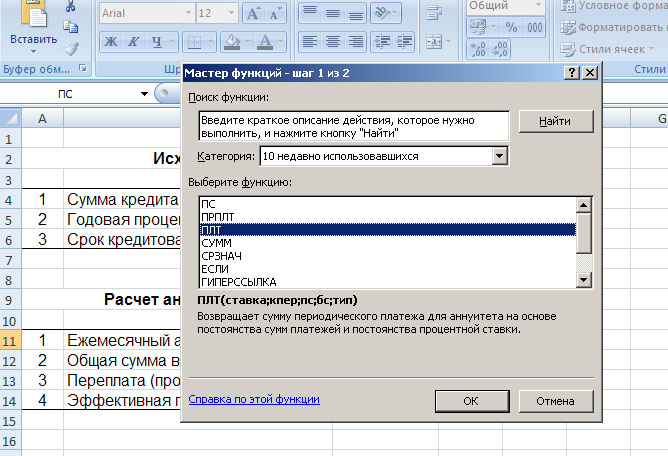
Начнём с расчёта ежемесячной суммы аннуитетного платежа. Для этого надо сделать активным окошко, в котором вы хотите видеть это значение (в нашем случае – это поле C11, на рисунке оно обведено и указано под номером 1). Далее слева от строки формул жмём на «fx» (на рисунке эта кнопка обведена и указана под номером 2). После этих действий у вас появится такая табличка:
Выбираем функцию «ПЛТ» и жмём «Ок». Перед вами появится таблица, в которую надо будет ввести исходные данные:
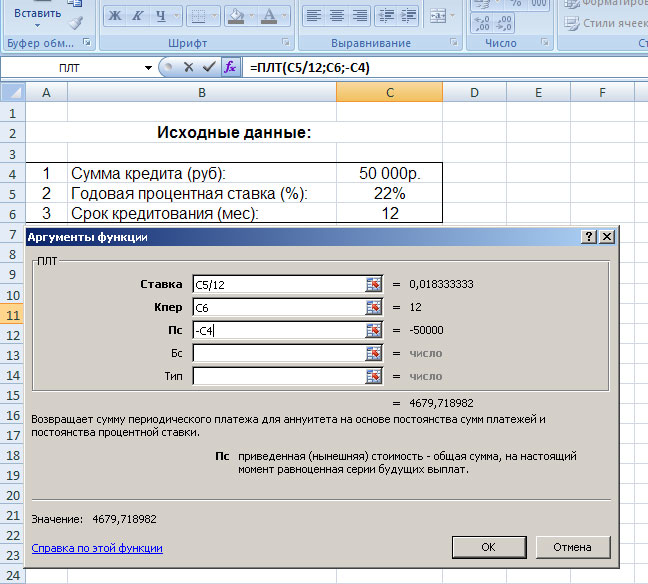
Здесь нам требуется заполнить три поля:
Обратите внимание на то, что мы не вводим готовые цифры в эту таблицу, а указываем координаты ячеек нашего блока с исходными данными. Так, в поле «Ставка» мы указываем координаты ячейки, в которой будет вписываться вручную процентная ставка (C5) и делим её на 12; в поле «Кпер» указываются координаты ячейки, в которой будет вписываться срок кредитования (C6); в поле «Пс» – координаты ячейки в которой вписывается сумма кредита (C4). Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус.
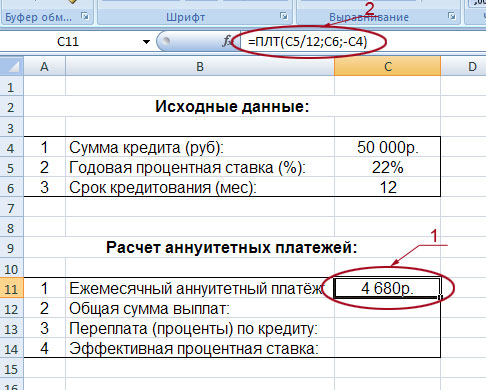
После того как исходные данные будут введены, жмём кнопку «Ок». В результате мы видим в блоке расчетов точное значение ежемесячного аннуитетного платежа:
Итак, в данный момент сумма нашего аннуитетного платежа составляет 4680 руб (на рисунке он обведён и указан под номером 1). Если вы будете менять сумму кредита, процентную ставку и общий срок кредитования, то автоматически будет меняться значение вашего аннуитетного платежа.
Кстати, обратите внимание на значение функции, обозначенное на рисунке под номером 2: =ПЛТ(C5/12;C6;-C4). Да, да, это и есть те самые координаты, которые мы вводили в таблицу, выбрав функцию «ПЛТ». По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках. Можно было просто вписать в строке формул то, что там сейчас вписано.
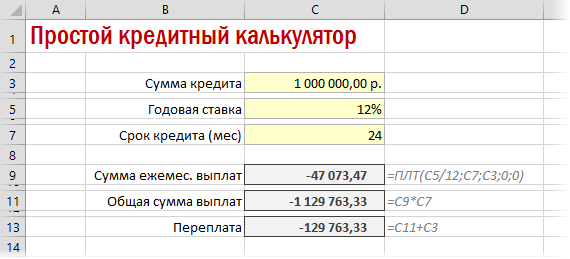
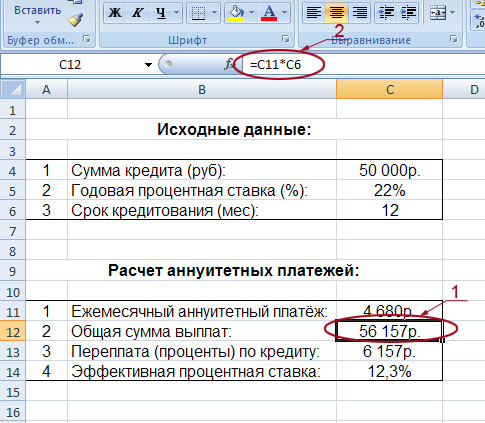
Зная размер аннуитетного платежа несложно посчитать остальные значения нашего расчётного блока:
На рисунке наглядно показано, как рассчитана общая сумма выплат (обведена и указана под номером 1). Так как она равна сумме аннуитетного платежа (ячейка C11) умноженной на общее количество месяцев кредитования (ячейка C6), то мы и вписываем в строку формул следующую формулу: =C11*C6 (на рисунке она обведена и указана под номером 2). В результате мы получили значение 56 157 рублей.
Переплата по кредиту рассчитывается ещё проще. От общей суммы выплат (ячейка C12) надо отнять сумму кредита (ячейка C4). В строку вписываем такую формулу: =C12-C4. В нашем примере переплата равна: 6157 рублей.
Ну и последнее значение – эффективная процентная ставка (или полная стоимость кредита). Она рассчитывается так: общую сумму выплат (ячейка C12) делим на сумму кредита (ячейка C4), отнимаем единицу, затем делим всё это на срок кредитования в годах (ячейка C6 делённая на 12). В строке будет такая формула: =(C12/C4-1)/(C6/12). В нашем примере эффективная процентная ставка составляет 12,3%.
Всё! Вот таким нехитрым способом мы с вами составили в программе Microsoft Excel автоматический калькулятор расчета аннуитетных платежей по кредиту, скачать который можно ссылке ниже:
Расчет в Excel суммы кредита для заданного аннуитетного платежа
В чём «фишка» аннуитетной схемы погашения кредита? Правильно! Основная «фишка» в том, что заёмщик выплачивает кредит равными суммами на протяжении всего срока кредитования. С такой схемой очень удобно планировать свой бюджет. Например, вы готовы ежемесячно выделять на погашение кредита 5000 рублей. По вашим скромным подсчётам, такая нагрузка будет для вас не слишком обременительной. Естественно, у вас возникает закономерный вопрос: «А на какую сумму кредита я могу рассчитывать?» В общем, нам нужен новый кредитный калькулятор, у которого в исходных данных будет не сумма кредита, а величина аннуитетного платежа.
Что же, друзья, не будем терять время! Открываем программу Microsoft Excel и приступаем к разработке нашего кредитного калькулятора!
Итак, структура нового кредитного калькулятора почти не изменилась. Здесь также есть блок с исходными данными и блок с расчётами. Единственное изменение, это то, что в исходных данных мы вводим ежемесячный аннуитетный платёж, который готовы выплачивать, а в расчётах получаем сумму кредита, на которую мы можем рассчитывать. Собственно, она на нашем рисунке обведена и отмечена под номером 1.
Чтобы рассчитать сумму ожидаемого кредита надо воспользоваться функцией ПС, предварительно кликнув по ячейке, в которой мы хотим видеть свой расчёт (в нашем калькуляторе это ячейка с координатой C11). Вызвать функцию ПС можно нажав на знакомую вам кнопку «fx», которая находится слева от строки формул. В появившемся окне выбираем «ПС» и жмём «Ок». В открывшейся таблице вводим следующие данные:
Жмём «Ок» и в ячейке С11 появилась сумма 53 422 руб. – именно на такой размер кредита может рассчитывать заёмщик, который готов на протяжении 12 месяцев ежемесячно выплачивать по 5000 руб.
Кстати, обратите внимание на данные в строке формул (на рисунке они обведены и указаны под номером 2). Вы всё правильно поняли, друзья! Да, это те данные, которые необходимы для расчёта суммы кредита в нашем калькуляторе: =ПС(C5/12;C6;-C4). Те самые параметры, которые мы вводили в таблице функции ПС.
Расчёт остальных показателей выполняется по такому же принципу, как и в предыдущем калькуляторе:
Кстати, интересный момент. Вот в нашем примере, выплачивая ежемесячно в течение года по 5000 рублей, мы можем рассчитывать на сумму кредита равную 53 422 рубля. А что делать, если надо больше денег? Как вариант, можно увеличить срок кредитования. Если вместо 12 месяцев поставить 24, то сумма кредита увеличится до 96 380 рублей. Эти данные нам мгновенно выдал наш кредитный калькулятор, который вы можете скачать ссылке ниже:
Кредитный калькулятор в Excel по расчету графика аннуитетных платежей
Два предыдущих кредитных калькулятора очень удобны, но они выполняют краткие (общие) расчёты. А иногда заёмщику нужна расширенная информация – график ежемесячных аннуитетных платежей с детальной расшифровкой каждой выплаты (с указанием сумм, идущих на погашение процентов, и сумм, погашающих тело кредита). В общем, сейчас мы сделаем в программе Excel ещё один кредитный калькулятор, который будет автоматически рассчитывать график аннуитетных платежей. Щёлкаем мышкой по рисунку:
Перед вами расширенная и доработанная версия нашего первого кредитного калькулятора (того, который рассчитывает размер ежемесячного аннуитетного платежа по кредиту). Здесь кроме стандартных блоков с исходными данными и расчётами, появилась таблица, в которой детально расписаны все наши будущие ежемесячные выплаты. Таблица имеет пять колонок:
Вот так легко и непринуждённо мы разработали кредитный калькулятор по расчёту графика аннуитетных платежей. Скачать его можно ссылке ниже:
Итак, друзья, теперь у вас есть целых три кредитных калькулятора по расчёту аннуитетных платежей, разработанных в программе Microsoft Excel. В следующей публикации мы расскажем о досрочном погашении аннуитетного кредита.