Сложный процент
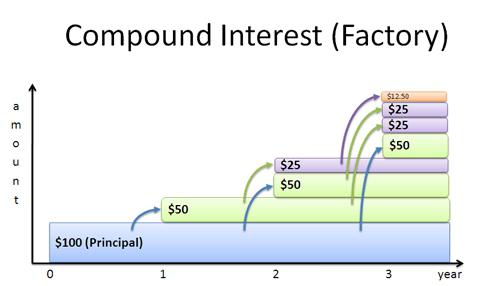
Сложным процентом принято называть эффект, когда проценты прибыли прибавляются к основной сумме и в дальнейшем сами участвуют в создании новой прибыли.
Формула сложного процента — это формула, по которой рассчитывается итоговая сумма с учётом капитализации (начислении процентов).
Простой расчет сложных процентов
Чтобы лучше усвоить расчет сложных процентов, давайте разберём пример.
Представим, что вы положили 10 000 руб в банк под 10 процентов годовых.
Через год на вашем банковском счету будет лежать сумма SUM = 10000 + 10000*10% = 11 000 руб.
Ваша прибыль — 1000 рублей.
Вы решили оставить 11 000 руб на второй год в банке под те же 10 процентов.
Через 2 года в банке накопится 11000 + 11000*10% = 12 100 руб.
Прибыль за первый год (1000 рублей) прибавилась к основной сумме (10000р) и на второй год уже сама генерировала новую прибыль. Тогда на 3-й год прибыль за 2-й год прибавится к основной сумме и будет сама генерировать новую прибыль. И так далее.
Этот эффект и получил название сложный процент.
Когда вся прибыль прибавляется к основной сумме и в дальнейшем уже сама производит новую прибыль.
Формула сложного процента:
SUM = X * (1 + %) n
где
SUM — конечная сумма;
X — начальная сумма;
% — процентная ставка, процентов годовых /100;
n — количество периодов, лет (месяцев, кварталов).
Расчет сложных процентов: Пример 1.
Вы положили 50 000 руб в банк под 10% годовых на 5 лет. Какая сумма будет у вас через 5 лет? Рассчитаем по формуле сложного процента:
SUM = 50000 * (1 + 10/100) 5 = 80 525, 5 руб.
Сложный процент может использоваться, когда вы открываете срочный вклад в банке. По условиям банковского договора процент может начисляться например ежеквартально, либо ежемесячно.
Расчет сложных процентов: Пример 2.
Рассчитаем, какая будет конечная сумма, если вы положили 10 000 руб на 12 месяцев под 10% годовых с ежемесячным начислением процентов.
SUM = 10000 * (1+10/100/12) 12 = 11047,13 руб.
ПРИБЫЛЬ = 11047,13 — 10000 = 1047,13 руб
Доходность составила (в процентах годовых):
% = 1047,13 / 10000 = 10,47 %
То есть при ежемесячном начислении процентов доходность оказывается больше, чем при начислении процентов один раз за весь период.
Если вы не снимаете прибыль, тогда начинает работать сложный процент.
Формула сложного процента для банковских вкладов
На самом деле формула сложного процента применительно к банковским вкладам несколько сложнее, чем описана выше. Процентная ставка для вклада (%) рассчитывается так:
% = p * d / y
где
p — процентная ставка (процентов годовых / 100) по вкладу,
например, если ставка 10,5%, то p = 10,5 / 100 = 0,105;
d — период (количество дней), по итогам которого происходит капитализация (начисляются проценты),
например, если капитализация ежемесячная, то d = 30 дней
если капитализация раз в 3 месяца, то d = 90 дней;
y — количество дней в календарном году (365 или 366).
То есть можно рассчитывать процентную ставку для различных периодов вклада.
Формула сложного процента для банковских вкладов выглядит так:
При расчете сложных процентов нужно принимать во внимание тот факт, что со временем наращивание денег превращается в лавину. В этом привлекательность сложных процентов. Представьте себе маленький снежный комок размером с кулак, который начал катиться со снежной горы. Пока комок катится, снег налипает на него со всех сторон и к подножию прилетит огромный снежный камень. Также и со сложным процентом. Поначалу прибавка, создаваемая сложным процентом, почти незаметна. Но через какое-то время она показывает себя во всей красе. Наглядно это можно увидеть на примере ниже.
Расчет сложных процентов: Пример 3.
Рассмотрим 2 варианта:
1. Простой процент. Вы инвестировали 50 000 руб на 15 лет под 20%. Дополнительных взносов нет. Всю прибыль вы снимаете.
2. Сложный процент. Вы инвестировали 50 000 руб на 15 лет под 20%. Дополнительных взносов нет. Каждый год проценты прибыли прибавляются к основной сумме.
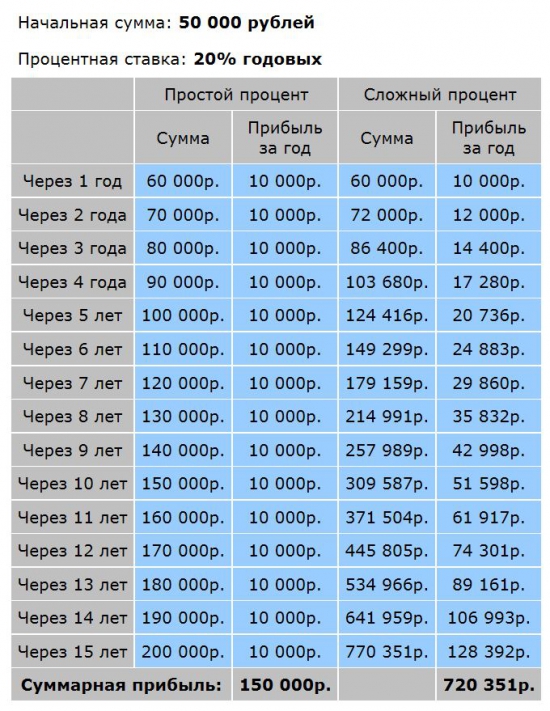  |
Комментарии, как говорится, излишни. Вложения с использованием сложного процента НА ПОРЯДОК выгоднее, чем с простым процентом. Чем больше проценты прибыли, чем дольше срок инвестирования, тем ярче проявляет себя сложный процент.
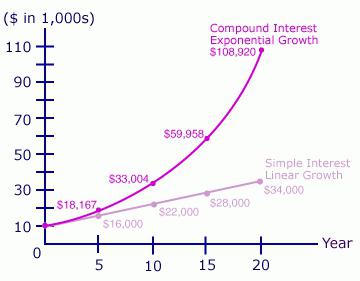
В случае простого процента график увеличения капитала получается линейный, поскольку вы снимаете прибыль и не даёте ей работать и приносить новую прибыль. В случае сложного процента график получается экспоненциальным, с течением времени кривая увеличения капитала становится всё круче, всё больше стремится вверх. Это происходит оттого, что из года в год прибыль накапливается и создаёт новую прибыль.
На графике ниже показано как вырастет капитал, если вложить 50 000 руб на 15 лет под 10%, 15% и 20%.
 |
Как видите, на длительном промежутке времени очень важным становится то, под какой процент вы инвестируете деньги.
Через 15 лет при 10% годовых 50 тысяч рублей превратятся в 200 тысяч, при 15% — уже в 400 тысяч, а при 20% годовых — в 780 тысяч.
Таким образом, сложный процент является мощным орудием по увеличению капитала на длительных промежутках времени.
Из формулы расчёта сложного процента можно выразить процентную ставку и количество лет (месяцев).
Процентная ставка:
Расчет сложных процентов: Пример 4.
Какая процентная ставка должна быть, чтобы за 10 лет 50 000 рублей превратились в 100 000 рублей?
% = (100000 / 50000) 1/10 — 1 = 0,0718 = 7,18 % годовых
Количество периодов (месяцев, лет):
n = log(1+0,4) (1000000 / 50000) = 8,9 лет
Как рассчитать проценты по займу
Как начисляются проценты по займу?
Какие есть варианты начисления процентов?
— вознаграждение в твердой сумме с единовременной либо ежемесячной выплатой;
— начисление процентов на всю сумму долга в течение срока займа, без учета ее погашения;
— начисление процентов может быть договором не предусмотрено. В этом случае ( но только если это не безвозмездный займ, при котором максимальная сумма долга ограничена 50 МРОТ и который может быть выдан только одним физическим лицом другому), проценты будут начисляться по ставке рефинансирования Банка России, которая с 1 января 2016 года равна ключевой ставке.
Что такое сложные проценты?
Пример расчета процентов
Чтобы правильно рассчитать проценты по договору займа необходимо знать сумму займа, срок, процентную ставку, а также порядок уплаты процентов. Как правило, в большинстве случаев процентные платежи являются ежемесячными и реже – ежеквартальными. Особые условия по начислению процентов могут быть предоставлены при займе безработным, а также когда порядок уплаты процентов в договоре не оговорен. В этом случае по умолчанию проценты начисляются и уплачиваются ежемесячно. Для тех кто решается взять взять займ без работы рекомендуется изучить расчет процентов по займу.
Как рассчитать проценты по займу в зависимости от способа их начисления?
1. Формула для расчета простых процентов выглядит следующим образом:
Сумма процентов по займу = Сумма займа * Процентная ставка / 365 (366) дней * Количество дней пользования займом;
2. Сложные проценты ( иначе говоря капитализированные) рассчитываются путем умножения изначальной суммы займа на величину, равную ( 1+r)n, где r – процентная ставка ( выраженная в долях), а n – количество прошедших платежных периодов.
Следует понимать, что итоговая формула расчета будет отличаться в зависимости от того, фиксированная либо плавающая ставка предусмотрена по договору займа. Расчет процентов с использованием плавающей ставки будет более затруднительным, но займы с подобной ставкой оформляются в настоящее время крайне редко, и наиболее часто ставка является фиксированной.
Крайне важным в процессе обслуживания долга является осуществление всех предусмотренных договором платежей в строго оговоренные сроки. В случае их нарушения условиями всех договоров займа предусмотрена неустойка (пени). Штраф за просрочку также учитывается при расчете итоговой суммы процентов по займу. Согласно закону «О потребительском кредита ( займе)» максимальный размер неустойки не может превышать 20% годовых ( 0,05% в день). В случае, если условиями договора неустойка не оговорена, ее расчет производится по размеру ключевой ставки Банка России, информацию о значении которой возможно узнать на официальном сайте регулятора.
Формула сложных процентов для кредита. Сложный процент: формула
Большая часть кредитов сегодня погашается с помощью аннуитентных платежей, одинаковых ежемесячных сумм. Аналогично и на вклады осуществляется стабильное начисление процента. Одна и та же сумма каждый месяц. В банковской практике такое начисление процентов называется простым. Таким образом, в случае с кредитом ежемесячно его владелец должен будет погашать не только часть основной суммы, но и насчитанный процент за ее пользование. Такой формат партнерства является законным. Совсем другое дело, если с заемщика снимается сложный процент. Формула его расчета будет рассмотрена ниже.
Против закона, или Как банки наживаются за счет неопытных заемщиков?
Многим будет интересно узнать, но начисление сложного процента на кредит – это незаконно. Такой формат сотрудничества делает банковский продукт весьма прибыльным для финансовых институтов и полностью убыточным для клиента. Незаконный формат начисления процента осуществляется тогда, когда процентная ставка на протяжении всего срока кредитования систематически меняется. Заметить неправомерные действия банка возможно только при формировании просрочки, которой по факту быть не должно. В ходе судебных разбирательств можно доказать, что банк начислял не совсем правильный процент.
Формула сложных процентов для кредита позволит понять, что начисление осуществляется не только на основную сумму долга, но и на сумму средств, которая была образована после начисления банковского процента. Говоря проще, сложные проценты представляют собой проценты, которые начисляются сами на себя. В банковской практике их еще называют двойными процентами.
Люди часто сталкиваются с ситуациями, когда их небольшой долг превращается в кругленькую сумму средств. Суть проблемы в том, что после того как финансовый институт зафиксирует просрочку, он присоединит к сумме долга процент. Следующее начисление будет осуществлено на основную сумму долга плюс насчитанный ранее на нее процент. Долг перед банком увеличивается в геометрической прогрессии. Невыгодные сложные проценты для заемщика становятся настоящим преимуществом для вкладчиков, так как аналогично увеличению долга они обеспечивают быстрый прирост прибыли.
Сложный процент: формула для заемщиков
В финансовой практике весьма распространена схема расчета сложных процентов. Она актуальна в том случае, если процентные средства не выплачиваются каждый месяц, а прибавляются к размеру основной задолженности, которая становится новой базой для начислений банка. Если ссуда имеет продолжительность от года и более, заемщик может столкнуться со своей неплатежеспособностью.
Помогает посчитать сложный процент формула, представленная ниже. Она ориентирована под анализ только одного периода начисления.
FV = PV + % = PV + PV * % = PV * (1 + %)
Для подсчета переплаты за два периода начисления можно использовать следующую формулу:
FV = (PV + %) * (% + 1) = PV * (1 + %) * (1 + %) = PV * (1 + %) 2
Посчитать объем переплаты за любое другое количество периодов поможет формула расчета сложных процентов:
FV = PV * (1 + %) N = PV * Кн, где:
Наращивание простых и сложных процентов
Формулы простых и сложных процентов позволяют определить объемы переплаты и предварительно оценить выгоды банковского продукта. При краткосрочных займах простые проценты оказываются более выгодными для банков. Однако если срок кредитования имеет среднесрочные или долгосрочные тенденции, разница может быть весьма ощутима для клиента. Отсюда выплывают следующие закономерности:
Независимо от процентной ставки при:
Как видим, финансовые институты, выдающие кредиты, получают больше выгоды от простых процентов при начислении всего дохода один раз к окончанию всего срока кредитования. Сложный процент приносит выгоды только если кредитование осуществляется не менее года. Оба типа процентов дают идентичную прибыль банку, если кредит оформлен на срок в один год, а проценты начисляются один раз по окончании партнерства.
Формула сложных процентов по вкладам
Сложные проценты используются банками не только для получения выгоды от кредитования. Формат начислений применяется и при оформлении вкладов, тем самым определяя выгоды для инвесторов. Итоговую сумму вклада можно рассчитать используя следующую формулу:
S = D * (1 + % * i / Y / 100 ) * N
Для расчета прибыли по вкладу эффективно использовать другие формулы:
Для сравнения прибыльности по вкладам, которые оформлены на разный период и для каждого из которых свойственна своя ставка сложных процентов, формула будет выглядеть иначе. Она позволит определить процент, который получит инвестор после капитализации.
Итоговая ставка банка, рассчитанная с учетом капитализации процента, называется эффективной. Финансовые институты не учитывают день окончания партнерства, если используют сложную схему начисления прибыли.
Пример расчета сложных начислений по вкладу
Формула начисления сложных процентов помогает каждому вкладчику предварительно оценить объем своего дохода. Попробуем рассчитать общий объем вклада и отдельно полученную по нему прибыль, если размер первичной инвестиции составлял 100 000 рублей на период 90 дней со ставкой 16 %.
S = 100000 + (100000 * 16 % * 90 / 365)
Sp = 100000 * 16 % * 90 / 365
На что обращать внимание?
Для каждого формата партнерства с банком нужно использовать индивидуальный вариант расчета. В зависимости от продолжительности вклада и периодичности выплат будет формироваться итоговый сложный процент. Формула его расчета будет изменяться от случая к случаю. Чтобы не допустить ошибок и выбрать максимально выгодную программу депозитов, нужно обратиться к экспертам. Помочь в данном вопросе могут представители финансового института. Они хоть и не имеют права рекомендовать вклады, но обязаны предоставить по просьбе полную схему расчета процентов по ним.
Капитализация при инвестировании в валютные рынки
Капитализация процентов встречается не только в банке, но и на валютном рынке «Форекс». Инвесторы, отдающие свои капиталы в доверительное управление, получают возможность следить за увеличением своих депозитов в геометрической прогрессии. Специфика данного вида инвестирования в том, что при получении прибыли она не снимается сразу, а распределяется по окончании торгового периода. На протяжении торгового периода, который может составлять неделю, месяц и даже несколько месяцев, будет автоматически проводиться начисление сложных процентов в силу специфики торговли. Для точного расчета дохода не подойдет формула сложных процентов по вкладам. Причина в отсутствии стабильной ставки. Прибыль определяется качеством торговли управляющего, его стратегией и политикой мани-менеджмента, прочими параметрами торговой системы.
Инвестору на заметку
Для расчета дохода при капитализации используется не одна формула сложных процентов для кредита и депозита, а несколько. Это обусловлено разными условиями партнерства с банком. Начисление процента на процент может проводиться каждый день, что является большой редкостью, каждую неделю, каждый месяц и даже каждый год (при долгосрочных инвестициях).
Оптимальным вариантом можно считать депозит с ежемесячной капитализацией, найти его несложно, а выгоды он принесет достаточно большие. Начисление процента на процент является тем выгодней для инвестора, чем чаще осуществляется начисление. Несмотря на более низкие процентные ставки по продуктам банка с капитализацией, прибыль в конечном счете получается на порядок больше, нежели при простой схеме начисления.
Еще один интересный момент заключается в том, что чем дольше вклад будет находиться в банке, тем быстрее он будет расти. Увеличение дохода будет происходить благодаря присоединению начислений к базовому объему средств. Если в течение года преимущества капитализации будут не так ощутимы, спустя десяток лет сомнения в преимуществах этого банковского предложения отпадут. Таким образом, выбирая меньшую процентную ставку, но останавливаясь на капитализации, можно получить более высокую прибыль по вкладу.
Сложный процент — главный секрет богатства! Формулы, Excel-калькулятор
Привет всем читателям Блога Вебинвестора! Думаю, каждый из вас сталкивался с начислением процентов на денежную сумму — по депозиту, по кредиту, расчётом доходности инвестиций и так далее. Так вот, если повторить эту процедуру много раз, вложения начинают расти всё быстрее и быстрее благодаря эффекту сложного процента! Воистину, это один из главных секретов, как с помощью инвестирования увеличить количество нулей в сумме на вашем банковском счёте.
Эта статья входит в бесплатное обучение инвестициям с нуля на Блоге Вебинвестора. В комментариях к статье вы можете оставлять любые вопросы по теме и я постараюсь подробно на них ответить.
Спасибо за внимание, продолжаем!
Что такое простой и сложный процент
и чем они отличаются
Понятие простых и сложных процентов — один из самых важных уроков по финансовой грамотности, которые вы должны знать. Они встречаются в нашей жизни повсюду: от ежедневных покупок (кэшбек, бонусы) до инвестирования (проценты на депозит, дивиденды, комиссии и т.д.) и оказывают незаметное, но существенное влияние на ваш кошелек на длинной дистанции. Чтобы наглядно увидеть различия между простыми и сложными процентами, давайте рассмотрим примеры.
Простой процент — прибыль в % начисляется только на первоначальную сумму вклада и сразу выводится.
Допустим, вы открыли депозит 10000$ под 10% годовых, проценты начисляются раз в год. По схеме простого процента каждые 12 месяцев вы будете получать 1000$ прибыли, но она не остаётся на депозите и сразу же выводится. В итоге прирост прибыли будет выглядеть так:
Всё «просто» — каждый год плюс тысяча в карман. Простой процент используется в случаях, когда база начисления процентов не изменяется. Это могут быть специальные банковские депозиты, проценты по кредиту. Также простой процент используется, когда инвестор регулярно выводит прибыль — в каждый период времени работает первоначальная сумма.
Сложный процент — проценты начисляются на первоначальную сумму вклада плюс всю полученную до этого прибыль. Понятия «реинвестирование» и «капитализация» по сути означают использование сложного процента.
Для сравнения пусть будет тот же депозит 10000$ под 10%, но банк в этот раз разрешает оставить прибыль на счёте. Вот что произойдёт с вкладом за 10 лет:
В первый год разницы нет — всё та же тысяча, но поскольку сумма на депозите теперь растёт, уже на втором году прибыль увеличивается: 2100$ вместо 2000$, за третий год 3310$ вместо 3000$ и так далее. За 10 лет доходность нашего депозита составила 159% вместо 100% когда мы выводили прибыль. Неплохая прибавка, не так ли? А вот что случится еще через несколько десятилетий:
Впечатляет! Чем дольше открыт депозит, тем сильнее работает эффект сложного процента — за 50 лет можно увеличить депозит не в 6, а более чем в 100 раз. Вот как это выглядит на графике:
без капитализации депозит растёт линейно,
а с капитализацией — по экспоненте
Теперь киношные истории про забытые банковские счета, на которых накопились миллионы долларов выглядят вполне реальными 
Думаю, суть понятна, теперь давайте пройдемся по математической стороне вопроса, а потом рассмотрим несколько типичных примеров задач.
Формулы простых и сложных процентов
Поскольку простые и сложные проценты чаще всего используются при расчете прибыли от банковских вкладов, продолжим на их примере. Для решения задач нам понадобится такая информация:
Формула простого процента
По этой формуле мы можем рассчитать конечную сумму вклада без капитализации полученной прибыли. Для этого нужно знать начальную сумму вклада, процентную ставку за 1 период инвестирования и временной интервал. Если конечная сумма задана сразу и нужно найти другую неизвестную переменную, используйте производные формулы простого процента:
Формула сложного процента
По этой формуле мы можем посчитать конечную сумму вклада с учётом капитализации полученной прибыли, зная начальный депозит, процентную ставку и нужный временной интервал. Для решения задач также можно использовать производные формулы сложного процента:
На практике часто дело не заканчивается первоначальным депозитом — многие пользуются регулярными пополнениями, например делают регулярные инвестиции из зарплаты. Для этих случаев формула сложного процента становится длиннее:
где D — сумма регулярных пополнений банковского депозита. Обратите внимание, степень N-1 означает, что доливки начинаются со второго инвестиционного периода (если сумма дополнительных инвестиций вносится сразу, то N-1 меняется на N).
Ну что, удачи на экзаменах всем читающим меня студентам 
Примеры решения задач
по сложным процентам
В этом разделе мы пройдемся по некоторым типичным задачам на сложные проценты. Также вы найдете шаблоны расчётов в Excel, в которых можно поменять вводные данные и получить нужное вам решение.
Задача №1. Рассчитать прибыль по вкладу на 5 лет под 10% годовых, начальная сумма вложений 100000 рублей (с капитализацией).
Находим конечную сумму вклада по формуле сложных процентов:
Результат: инвестор через 5 лет получит 61051 рублей прибыли.
Задача №2. Рассчитать прибыль по вкладу на 10 лет под 10% годовых с капитализацией. Начальная сумма вложений 50000 рублей, дополнительно каждый год начиная с первого счёт пополняется на 10000 рублей.
Сначала находим конечную сумму по формуле сложного процента с регулярными пополнениями:
Учитывая, сколько инвестировано за 10 лет (50000 сразу и еще 9 раз по 10000), вычисляем прибыль:
Результат: инвестор через 10 лет получит 139061 рубль прибыли, инвестировав 140000 рублей.
Задача №3. Рассчитать, сколько времени понадобится инвестору, чтобы увеличить капитал с 500000 до 1000000 рублей. Средняя доходность портфеля — 12% годовых, прибыль реинвестируется.
У нас есть все необходимые данные, используем одну из производных формул сложных процентов:
Решение: инвестору понадобится чуть больше 6 лет.
Задача №4. Посчитать среднюю процентную ставку, которая позволит превратить 100000 рублей в 500000 рублей за 10 лет путём инвестирования. Прибыль реинвестируется.
Используем одну из производных формул сложных процентов:
Решение: инвестору нужно вложить деньги под 17.5% годовых (довольно сложно на практике, кстати).
Думаю, этого достаточно. Если ваша задача не похожа ни на одну из предыдущих, возможно вам поможет информация из следующего раздела статьи.
Калькулятор сложных процентов в Excel
Конечно же, задачи на сложные проценты целесообразнее решать в MS Excel по уже известным вам из предыдущих разделов формулам. По ходу статьи вы уже могли скачать некоторые примеры типичных задач, но если этого мало — предлагаю полную подборку калькуляторов по сложным процентам, реализованную в одном Excel-файле. Получить его можно бесплатно, просто заполните форму ниже:
Если письмо не пришло, проверяйте папку «Спам», иногда попадает туда. Если не видите форму подписки, оставьте комментарий к статье и я добавлю ваш электронный адрес вручную.
Вот какие задачи по простым и сложным процентам может решать «Коллекция калькуляторов для инвестора»:
В будущем я планирую добавить много калькуляторов по самым разным темам, оставляйте свои пожелания в комментариях!
Пример одного из калькуляторов для расчёта сложных процентов в Excel:
Дополнительно к каждому калькулятору автоматически строится график доходности вклада с капитализацией и без:
А также уже знакомые вам таблицы:
Думаю, файл будет полезен и для практического использования, и в обучающих целях — в готовом виде есть все формулы, по которым можно считать сложные проценты в Excel.
Как использовать сложные проценты
в инвестировании
Как вы уже знаете, получаемая от инвестиций прибыль — это важный инструмент, который на большой дистанции может во много раз увеличить доходность ваших вложений. Метод повторного вложения прибыли называется реинвестированием.
Безусловно, использовать эффект сложного процента должен каждый инвестор, однако на практике это не так просто как кажется. Существует несколько проблем, которые мешают теоретически супервыгодное реинвестирование реализовать в реальных условиях. Например, вряд ли вы слышали о людях, ставших миллиардерами через банковские депозиты. Дело в том, что деньги постоянно обесцениваются из-за инфляции — постоянного повышения цен на товары и услуги. На самом деле ставка банковских депозитов обычно примерно равна инфляции или даже ниже, поэтому реальная доходность вкладов не впечатляет:
Даже если оставить удачный бескризисный отрезок 2010-2020 годов, доходность банковского вклада с учётом инфляции была в районе 1-2% годовых в рублях. Не говоря уже о доходности в долларах, которая после 2014 года, очевидно, находится в еще большем минусе.
Кроме инфляции сильно повлиять на итоговую доходность инвестиций могут разнообразные комиссии. Если их размер зависит от суммы инвестиций, убытки накапливаются по правилу сложных процентов, но уже с негативным эффектом. Это значит, что за несколько десятков лет инвестор может потерять сотни или даже тысячи процентов прибыли.
Такое часто встречается при инвестициях в ETF, где комиссия за управление достигает несколько процентов от депозита в год. Один из самых старых ETF под тикером SPY (инвестиционная стратегия — следование за индексом S&P 500) работает с 1993 года и берет с клиентов 0.09% в год — немного, по сравнению с другими биржевыми фондами. Эта ставка со временем может меняться, но давайте для эксперимента представим что она всегда была такой — и сравним, как будет отличаться доходность инвестиций при комиссиях от 0 до 2% в год:
Как видите, даже из-за несчастных 0.09% инвестор на дистанции 27 лет потерял 25% прибыли. А вроде бы небольшая комиссия в 2% годовых срезает доходность почти в 3 раза — с 723% до 270%, и это еще не учтена инфляция. По причине скрытых комиссий высокая доходность активов на самом деле может оказаться в разы ниже, поэтому перед принятием решения об инвестировании важно учитывать даже мизерные расходы.
Куда же стоит инвестировать, чтобы использовать эффект сложного процента на максимум и минимизировать влияние инфляции и комиссий? Я бы выделил такие инструменты:
Оптимальный портфель инвестора предполагает использование всех этих инструментов, поскольку генерируемый ими денежный поток позволяет гибко управлять вложениями: делать ребалансировку, выводить прибыль или реинвестировать. Использовать правило сложных процентов можно в любых инвестициях, но не везде это рекомендуется делать. Чем выше риски вложений, тем выгоднее просто выводить прибыль, поскольку при неудачных раскладах депозит может быть потерян.
Использование сложных процентов — теоретически очень выгодное занятие, но как всегда дьявол кроется в деталях. Тем не менее, реинвестирование/капитализация остаётся одним из главных инструментов для накопления большого капитала, грех его игнорировать. И даже вне инвестирования начисление процентов по простому или сложному принципу встречается часто, поэтому полезно знать как это все работает. Надеюсь, подробный разбор формул и решения задач будут вам полезны.