формула тейлора с остатком в форме пиано - Операционные системы и программное обеспечение

Формула Тейлора

Формула Тейлора с остаточным членом в форме Лагранжа.

Если функция $f(x)$ имеет в точке $x_<0>$ производную n-го порядка, то существует многочлен $P_(x)$ степени не выше n такой, что
$$
P_n(x_0)=f(x_<0>),\ P_^<(k)>(x_<0>)=f^<(k)>(x_<0>),\ k=\overline<1,n>.\label
$$
Этот многочлен представляется в виде
$$
P_n(x)=f(x_<0>)+\frac)><1!>(x-x_0)+\frac<2!>(x-x_0)^2+\ldots+\frac(x_0)>(x-x_0)^n.\label
$$

$\circ$ Пусть $\varphi(x)=(x-x_0)^m$, где $m\in\mathbb$. Тогда $\varphi(x_0)=0$,
$$
\varphi^<(k)>(x_<0>)=\left\<\begin
0, & если \ k\neq m,\\
k!, & если \ k=m.
\end\right.\label
$$
Из \eqref следует, что многочлен $P_n(x)$, заданный формулой \eqref, удовлетворяет условиям \eqref. Этот многочлен называют многочленом Тейлора n-го порядка для функции $f(x)$ в точке $x_<0>$. $\bullet$

Пусть функции $f(x)$ и $\psi(x)$ определены в $\delta$-окрестности точки $x_0$ и удовлетворяют следующим условиям:

Тогда для каждого $x\in\dot_<\delta>(x_<0>)$ существует точка $\xi$, принадлежащая интервалу с концами $x_0$ и $x$ такая, что
$$
\frac<\varphi(x)><\psi(x)>=\frac<\varphi^<(n+1)>(\xi)><\psi^<(n+1)>(\xi)>.\label
$$

$\circ$ Пусть, например, $x\in(x_0,x_0+\delta)$. Тогда, применяя к функциям $\varphi$ и $\psi$ на отрезке $[x_0,x]$ теорему Коши и учитывая, что $\varphi(x_0)=\psi(x_0)=0$ в силу условий \eqref, получаем
$$
\frac<\varphi(x)><\psi(x)>=\frac<\varphi(x)-\varphi(x_0)><\psi(x)-\psi(x_0)>=\frac<\varphi'(\xi_1)><\psi'(\xi_1)>\quad x_0 Теорема 1.

Пусть существует $\delta >0$ такое, что функция $f(x)$ имеет в $\delta$-окрестности точки $x_0$ производные до $(n+1)$-го порядка включительно.

Тогда для любого $x\in\dot_\delta(x_0)$ найдется точка $\xi$, принадлежащая интервалу $\Delta$ с концами $x_<0>$ и $x$, такая, что
$$
f(x)=f(x_0)+\frac)><1!>(x-x_0)+\ldots+\frac(x_<0>)>(x-x_0)^n+\frac(\xi)><(n+1)!>(x-x_<0>)^.\label
$$

$\circ$ Пусть $x\in\dot_\delta(x_0)$, $P_n(x)=\displaystyle \sum_^\frac(x_<0>)>(x-x_0)^k$ — многочлен Тейлора для функции $f(x)$. Обозначим
$$
r_(x)=f(x)-P_n(x).\label
$$
Так как многочлен $P_(x)$ удовлетворяет в силу леммы 1 условиям \eqref, то из равенства \eqref следует, что
$$
r_n(x_0)=r_n'(x_0)=\ldots=r_^<(n)>(x_<0>)=0.\label
$$
Рассмотрим функции $\varphi(x)=r_n(x)$, $\psi(x)=(x-x_0)^$. Эти функции удовлетворяют условиям леммы 2, и поэтому для них выполняется равенство \eqref, то есть
$$
\frac<\varphi(x)><\psi(x)>=\frac<(x-x_0)^>=\frac(\xi)><(n+1)!>=\frac(\xi)><(n+1)!>,\quad\xi\in\Delta,\label
$$
так как $P_n^<(n+1)>(x)\equiv 0,\ \psi^<(n+1)>(x)=(n+1)!$ Из равенств \eqref и \eqref следует формула \eqref. $\bullet$

Функцию $r_n(x)=\displaystyle \frac(\xi)><(n+1)!>(x-x_0)^$ называют остаточным членом формулы Тейлора в форме Лагранжа. Формула \eqref справедлива и при $x=x_<0>$.

Если функции $\varphi$ и $\psi$ дифференцируемы $n$ раз при $x\geq x_<0>$ и удовлетворяют условиям $\varphi^<(k)>(x_<0>)=\psi^<(k)>(x_<0>)$, $k=\overline<0,n-1>$, $\varphi^<(n)>(x)>\psi^<(n)>(x)$ при $x > x_0$, то $\varphi(x) > \psi(x)$ при $x > x_<0>$.

$\circ$ Для $n=1$ утверждение доказано ранее (следствие 4 из теоремы Лагранжа). Обозначим $f(x)=\varphi(x)-\psi(x)$. Тогда $f^<(k)>(x_<0>)=0$ при $k=\overline<0,n-1>0$, и по формуле \eqref получаем
$$
f(x)=\frac<1>(x-x_<0>)^f^<(n)>(\xi).\nonumber
$$
Если $ x> x_<0>$, то $\xi > x_0$, $f^<(n)>(\xi)=\varphi^<(n)>(\xi)-\psi^<(n)>(\xi) > 0$, и поэтому $f(x) > 0$, то есть $\varphi(x) > \psi(x)$ при $x > x_<0>$. $\bullet$

Формула Тейлора с остаточным членом в форме Пеано.

Из существования $f^<(n)>(x_0)$ следует, что функция $f(x)$ определена и имеет производные до $(n-1)$-го порядка включительно в $\delta$-окрестности точки $x_0$. Обозначим $\varphi(x)=r_n(x)$, $\psi(x)=(x-x_0)^n$, где функция $r_n(x)$ определяется формулой \eqref. Функции $\varphi(x)$ и $\psi(x)$ удовлетворяют условиям леммы 2, если заменить номер $n+1$ на номер $n-1$ (см. равенства \eqref). Используя лемму 2 и учитывая, что $r_n^<(n-1)>(x_0)=0$, получаем
$$
\frac<(x-x_0)^n>=\frac(\xi)-r_n^(x_0)>)>,\label
$$
где $\xi=\xi(x)$ и
$$
x_0 Замечание 2.

Формулу \eqref часто называют формулой Тейлора с остаточным членом в форме Пеано или локальной формулой Тейлора.

Разложить функцию $f(x)$ по формуле Тейлора в окрестности точки $x_0$ до $o((x-x_0)^n)$ — значит представить ее в виде \eqref.

$\circ$ По теореме 2 справедлива формула \eqref, и так как по условию выполняется равенство \eqref, то
$$
a_0+a_1(x-x_0)+\ldots+a_n(x-x_0)^n+o((x-x_0)^n)=\\=f(x_<0>)+f'(x_<0>)(x-x_0)+\ldots+f^<(n)>(x_<0>)\frac<(x-x_<0>)^>+o((x-x_0)^n).\label
$$
Переходя к пределу при $x\rightarrow x_<0>$ в равенстве \eqref, получаем $a_<0>=f(x_<0>)$. Отбросив в левой и правой частях этого равенства одинаковые слагаемые $a_<0>$ и $f(x_<0>)$ и разделив обе части полученного равенства на $x-x_0$, имеем
$$
a_1+a_2(x-x_0)+\ldots+a_n(x-x_0)^+o((x-x_0)^)=\\=f'(x_0)+\frac)><2!>(x-x_0)+\ldots+\frac(x_<0>)>(x-x_0)^+o((x-x_0)^).
$$
Переходя в этом равенстве к пределу при $x\rightarrow x_0$, находим $f'(x_<0>)=a_<1>$. Продолжая эти рассуждения, получаем равенства \eqref. $\bullet$

Теорема 3 означает, что представление в виде \eqref функции, имеющей в точке $x_<0>$ производную $n$-го порядка, единственно: коэффициенты разложения \eqref выражаются по формулам \eqref.

Разложить функцию $\displaystyle \frac<1><1-x>$ по формуле Тейлора в окрестности точки $x_<0>=0$ до $o(x^)$.

$\triangle$ Воспользуемся равенством $(1+x+\ldots+x^)(1-x)=1-x^$, откуда $\displaystyle \frac<1><1-x>=1+x+\ldots+x^n+r_n(x)$, где $r_n(x)=\displaystyle \frac><1-x>=o(x^)$ при $x\rightarrow 0$. Таким образом,
$$
\frac<1><1-x>=1+x+\ldots+x^n+o(x^n).\label
$$
Так как функция $\displaystyle \frac<1><1-x>$ бесконечно дифференцируема при $x\neq 1$ (имеет производные любого порядка), то по теореме 3 формула \eqref дает искомое разложение. $\blacktriangle$

Разложение основных элементарных функций по формуле Тейлора.

Если $x_<0>=0$ и существует $f^<(n)>(0)$, то равенство \eqref принимает вид
$$
f(x)=\sum_^\frac>x^k+o(x^n),\ x\rightarrow 0.\label
$$
Формулу \eqref называют формулой Маклорена.

Пусть, функция $f(x)$ бесконечно дифференцируема на интервале $(-l,l)$. Если эта функция является четной, то ее производная — нечетная функция, и, наоборот, производная нечетной функции — четная функция (мы уже разбирали этот пример). Отсюда следует, что для нечетной функции $f$ выполняются условия $f^<(2k)>(0)=0$, $k\in\mathbb$, а для четной функции $f$ — условия $f^<(2k-1)>(0)=0$, $k\in\mathbb$, так как любая непрерывная нечетная функция принимает при $x=0$ значение нуль.

Поэтому формулу \eqref для бесконечно дифференцируемой четной функции можно записать в виде
$$
f(x)=\sum_^\frac(0)><(2k)!>x^<2k>+o(x^<2n+2>),\quad x\rightarrow 0,\label
$$
а для нечетной функции — в виде
$$
f(x)=\sum_^\frac(0)><(2k+1)!>x^<2k+1>+o(x^<2n+2>),\quad x\rightarrow 0,\label
$$
В формуле \eqref остаточный член записан в виде $o(x^<(2n+1)>)$, а не в виде $о(x^<2n>)$, так как для четной функции $f$ выполняется условие $f^<(2n+1)>(0)=0$, и поэтому член многочлена Тейлора, который следует за слагаемым $\displaystyle\frac(0)><(2n)!>x^<2n>$ равен нулю. Аналогично рассматривается вопрос о записи остаточного члена формулы \eqref.

Показательная функция.

Гиперболические функции.

Так как $\operatornamex=\displaystyle \frac-e^<-x>><2>$, $\operatornamex=\displaystyle \frac+e^<-x>><2>$, то формулы \eqref и \eqref можно получить, используя равенство \eqref и равенство $e^<-x>=\displaystyle \sum_^\frac<(-1)^x^>+о(x^),\ x\rightarrow 0$.

Источник

Локальная формула Тейлора с остаточным членом в форме Пеано.

Ответ:

Теорема(формула Тейлора с остаточным членом в форме Пеано) Пусть — остаток в формуле Тейлора для функции в точке , и функция имеет непрерывную -ю производную. Тогда — бесконечно малая величина того же или большего порядка малости, как , при . (Остаточный член , о котором известны эти сведения о порядке малости, называется остаточным членом в форме Пеано.)

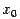
Доказательство. Утверждение теоремы означает, что существует

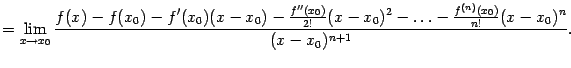При остаток будет иметь тот же порядок малости, что , а при — больший порядок малости. Итак, вычислим предел:

Применим к этому пределу правило Лопиталя, повторив этот приём раз:

Последний предел мы вычислили прямой подстановкой, поскольку по предположению — непрерывная функция. Существование предела доказывает утверждение теоремы.

27. Исследование функций с помощью первой и второй производной. Необходимое и достаточное условие экстремума функций:

Ответ:

Исследование функций с помощью производной.

Возрастание и убывание функций.

Теорема. 1) Если функция f(x) имеет производную на отрезке [a, b] и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е. f¢(x) ³ 0.

2) Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на промежутке (а, b), причем f¢(x) > 0 для a f(x) при Dx>0 и f(x + Dx) 0 для любых точек х₁ и х₂, принадлежащих отрезку [a, b], причем x₁ 0, следовательно, f(x₂) – f(x₁) >0, т.е. функция f(x) возрастает.

Аналогично можно сделать вывод о том, что если функция f(x) убывает на отрезке [a, b], то f¢(x)£0 на этом отрезке. Если f¢(x)

Определение. Функция f(x) имеет в точке х₁ максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку х₁. Функция f(x) имеет в точке х₂ минимум, если f(x₂ +Dx) > f(x₂) при любом Dх (Dх может быть и отрицательным).

Очевидно, что функция, определенная на отрезке может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные.

Определение. Точки максимума и минимума функции называются точками экстремума.

Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х₁ и точка х₁ является точкой экстремума, то производная функции обращается в нуль в этой точке.

Доказательство. Предположим, что функция f(x) имеет в точке х = х₁ максимум.

Тогда при достаточно малых положительных Dх>0 верно неравенство:

, т.е.

Т.е. если Dх®0, но Dх 0, то f¢(x₁) £ 0.

А возможно это только в том случае, если при Dх®0 f¢(x₁) = 0.

Для случая, если функция f(x) имеет в точке х₂ минимум теорема доказывается аналогично.

Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю.

Теорема. (Достаточные условия существования экстремума)

Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х₁, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х₁).

Если при переходе через точку х₁ слева направо производная функции f¢(x) меняет знак с “+” на “-“, то в точке х = х₁ функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет минимум.

Доказательство.

Пусть

По теореме Лагранжа: f(x) – f(x₁) = f¢(e)(x – x₁), где x 0; f¢(e)(x – x₁) x₁, то e > x₁ f¢(e)

Доказательство.

Пусть f¢(x₁) = 0 и f¢¢(x₁) 0 при х x₁. Это и означает, что при переходе через точку х = х₁ производная f¢(x) меняет знак с “+” на “-“, т.е. в этой точке функция f(x) имеет максимум.

Для случая минимума функции теорема доказывается аналогично.

Если f¢¢(x) = 0, то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование.

Дата добавления: 2015-01-19 ; просмотров: 29 ; Нарушение авторских прав

Источник

Формула Тейлора с остаточным членом в форме Пеано.

Формула Тейлора с остаточным членом в форме Пеано.

HT) y=1 ‘ 1 d’DH t Икс X f(x?2, x°… (T, x°t)+o (RP). Заметим, что справа от (12.59) (12.59) находится сумма полиномов » степени n переменной T x 2,…, HT и остаточный член o (RP). Разница между GN (M) CM) и обозначена.Многочлен, то есть GN (M)=f (M) — f(My) — п Теорема * 12.15 при условиях этой теоремы gn (M)=o (RP).§5. Производные более высокой степени и неравенство 501 Доказательству теоремы 12.15 *

Функция F f используется для образования частных производных от f и K C и p o N n o-й точки M0, а затем выделяется Xi. Людмила Фирмаль

Благодаря вышесказанному, чтобы доказать равенство(12.64), достаточно убедиться в справедливости равенства d D D x (Xi-xf) G n d1 * дифференциальная функция (XX+H°) — — — — — N D L dx! Учитывая независимость Xi символа D и■выше, мы получаем равенство (12.65). Индукционный Завер- И dhg По Си как Сиена. Лемма 1 доказана. Л е м м А2. G (M)=g (xi, x2,…, ХТ)имеет дополнительные функции, которые удовлетворяют двум требованиям:1) дифференциальные N раз с a4o(Си°, Х2°,…2) сама функция g (M) и все частные производные от любой переменной Xi, x2,…, HT order n inclusive,§5. Производные и дифференциал таможни 50 выше» Ноль в указанной точке МО. Тогда для функции g (M) справедлива оценка g (M)=o (pn), а в (12.66)

расстояние между точками M и Mo p (M, mo) обозначается п. для P-1 утверждение леммы следует из условия Дифференцируемости функции g(M) в точках Mo вида G(M)-g(M0)=^—^(M o) (X9-X9)+o(p). * См. пункт 12.16, отношение 2,§4 в этой главе. **То есть в множестве точек вида M0+t (M-L10), t-любое число из отрезка 01, а также действительна для числа n+1 в таких случаях. Так что функция g (M) удовлетворяет двум требованиям леммы 2d l I n o m er A n+1. Тогда ясно, что эта первичная функция (M), i=l, частный дифференциал 2…, ПГ, будет И dhg- Лемма удовлетворяет двум требованиям 2d l i n o m er a p, поэтому (благодаря предположениям, которые мы имеем о справедливости леммы 2 для нескольких p) Справедливая цитата

также oh!/ ( * ) 12.66 Заметим, что функция g(M), удовлетворяющая двум требованиям леммы 2 для чисел n>1, n+1>2 и N+1, дифференцируема по крайней мере один раз в окрестности Mo, поэтому для этой функции g (M) выполняется условие теоремы для числа n=0 12.15. Согласно этой теореме, для любой точки M из достаточно малой e окрестности точки Mo на отрезке*M0M справедливо уравнение m g (M)=g (Mo)+-y — A в такой точке N равно (L0. I=l1 Точка N находится между точками Mo и M, p — расстояние между точками L1o и M, p (N, ui0)) (12.66 это^ — W=o(Pn) — DX (504CH. 12. Функции некоторых переменных Подставляя последнюю цитату

для(12.67) и предполагая£(L40)= = 0、 Тонны g (M)=o (pnY)|xz-XP/. 1=1 Xt-x° / m s наконец — ‘ 1=1 предположим, что g(M)=o (pn+1). Индукция завершена. Лемма 2 доказана. Теорема 12. 15 * легко выполняется Леммой 1 и 2. Фактически, для доказательства теоремы 12.15, когда выполняются условия этой теоремы, достаточно доказать, что оцененное значение gn (M)=o (pn) справедливо для функции (12.60). Благодаря Лемме 1, сама функция(12.60) и все ее частные производные, поверх любой переменной XY×2…HT исчезает в порядке n включительно L40. Но тогда, благодаря Лемме 2 для функции(12.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Формула Тейлора для функций многих переменных

Формула Тейлора с остаточным членом в форме Лагранжа.

В дальнейшем будет удобно наделить метрическое пространство $\boldsymbol^$ еще и структурой линейного пространства, полагая для любых $x = (x_<1>, \ldots, x_)$, $y = (y_<1>, \ldots, y_)$ и $\alpha \in \boldsymbol$, что
$$
x+y = (x_<1>+y_<1>, \ldots, x_+y_),\ \alpha x = (\alpha x_<1>, \ldots, \alpha x_).\nonumber
$$
Легко проверяется, что для введенных подобным образом операций сложения элементов и умножения элементов на вещественные числа выполняются все аксиомы линейного пространства. Роль нулевого элемента выполняет $0 = (0, 0, \ldots, 0) \in \boldsymbol^$. Если $x = (x_<1>, \ldots, x_)$, $x^ <0>= (x_<1>^<0>, \ldots, x_^<0>)$, то по определению
$$
\Delta x = dx = x-x^ <0>= (x_<1>-x_<1>^<0>, \ldots, x_-x_^<0>) = (dx_<1>, \ldots, dx_),\nonumber
$$
$$
|\Delta x| = \sqrt<\Delta x_<1>^<2>+\ldots+\Delta x_^<2>> = \rho (x, x^<0>).\nonumber
$$

(Формула Тейлора с остаточным членом в форме Лагранжа).

Пусть функция $f(x)$ имеет в шаре $S_ <\delta>(x^<0>) \subset \boldsymbol^$ непрерывные частные производные всех порядков до $m$ включительно. Тогда для любой точки $x^<0>+\Delta x \in S_ <\delta>(x^<0>)$ найдется число $\theta \in (0, 1)$ такое, что справедливо следующее равенство (формула Тейлора с остаточным членом в форме Лагранжа):
$$
f(x^<0>+\Delta x) = f(x^<0>)+\sum_^ \fracf(x^<0>)>+r_(x),\label
$$
где
$$
r_(x) = \frac<1> d^f(x^<0>+\theta \Delta x),\label
$$
a $d^ f(\xi)$ есть дифференциал $k$-го порядка функции $f(x)$, вычисленный в точке $\xi$ и являющийся однородной формой $k$-го порядка относительно дифференциалов независимых переменных $dx_<1>, \ldots, dx_$:
$$
d^ f(\xi) = \left(dx_ <1>\frac<\partial><\partial x_<1>>+\ldots+dx_ \frac<\partial><\partial x_>\right)^ f(\xi) = \sum_ = 1>^ \ldots \sum_ = 1>^ \frac <\partial^f(\xi)><\partial x_> \ldots \partial x_>> dx_> \ldots dx_>.\label
$$

$\circ$ Если точка $x^<0>+\Delta x \in S_ <\delta>(x^<0>)$, то в силу симметрии шара и точка $x^<0>-\Delta x \in S_ <\delta>(x^<0>)$. Так как шар есть выпуклое множество, то $x^<0>+t\Delta x \in S_ <\delta>(x^<0>)$ при любом $t \in [-1, 1]$. Поэтому на [—1,1] определена функция одной переменной:
$$
\varphi(t) = f(x^<0>+t\Delta t) = f(x_<1>^<0>+t\Delta x_<1>, \ldots, x_^<0>+t\Delta x_).\nonumber
$$

Функция $\varphi(t)$ дифференцируема на отрезке [-1,1]. Действительно, применяя правило нахождения производной сложной функции, получаем
$$
\varphi'(t) = \sum_^ \frac<\partial f(x^<0>+t\Delta x)><\partial x_> \Delta x_ = df (x^<0>+t\Delta x) = \left(dx_ <1>\frac<\partial><\partial x_<1>>+\ldots+dx_ \frac<\partial><\partial x_>\right) f(x^<0>+t\Delta x).\label
$$
Аналогично
$$
\varphi″(t) = \sum_^ \sum_^ \frac <\partial^<2>f(x^<0>+t\Delta x)><\partial x_\partial x_> \Delta x_ \Delta x_ = d^<2>f (x^<0>+t\Delta x) =\\= \left(dx_ <1>\frac<\partial><\partial x_<1>>+\ldots+dx_ \frac<\partial><\partial x_>\right)^ <2>f(x^<0>+t\Delta x).\nonumber
$$
По индукции получаем, что для $k = \overline<1, m>$ справедливы формулы
$$
\varphi^<(k)>(t) = \sum_ = 1>^ \ldots \sum_ = 1>^ \frac <\partial^f(x^<0>+t\Delta x)><\partial x_> \ldots \partial x_>> dx_> \ldots dx_> =\\= d^f(x^<0>+t\Delta x) = \left(dx_ <1>\frac<\partial><\partial x_<1>>+\ldots+dx_ \frac<\partial><\partial x_>\right)^ f(x^<0>+t\Delta x).\label
$$

Применим к функции $\varphi(t)$ формулу Тейлора с остаточным членом в форме Лагранжа. Существует число $\theta \in (0, 1)$ такое, что
$$
\varphi(t) = \varphi(0)+t\varphi'(0)+\ldots+\frac> <(m-1)!>\varphi^<(m-1)>(0)+r_(t),\qquad r_(t) = \frac> \varphi^<(m)>(\theta t).\nonumber
$$

Полагая $t = 1$, получаем
$$
\varphi(1) = \varphi(0)+\varphi'(0)+\ldots+\frac<1> <(m-1)!>\varphi^<(m-1)>(0)+r_(1),\qquad r_(1) = \frac<1> \varphi^<(m)>(\theta).\nonumber
$$
Подставляя в эту формулу выражения \eqref для производных $\varphi^<(k)>(t)$ при $t = 0$, получаем формулу \eqref. $\bullet$

Если выполнены условия теоремы 1, то для функции $f(x)$ справедлива формула Тейлора с остаточным членом в форме Пеано
$$
f(x) = f(x^<0>)+\sum_^ \frac<1> d^f(x^<0>)+o(|\Delta x|^)\label
$$
при $|\Delta x| \rightarrow 0$, где $|\Delta x| = \sqrt<\Delta x_<1>^<2>+\ldots+\Delta x_^<2>>$.

$\circ$ Рассмотрим остаточный член в формуле \eqref:
$$
r_(x) = \frac<1> d^ f(x^<0>+\theta \Delta x) = \frac<1> \sum_ = 1>^ \ldots \sum_ <\substack= 1>>^ \frac <\partial^f(x^<0>+\theta\Delta x)><\partial x_> \ldots \partial x_>> \Delta x_> \ldots \Delta x_>.\label
$$
Так как по условию все производные порядка $m$ функции $f(x)$ непрерывны в точке $x_<0>$, то
$$
\frac <\partial^f(x^<0>+\theta\Delta x)><\partial x_> \ldots \partial x_>> = \frac <\partial^f(x^<0>)><\partial x_> \ldots \partial x_>>+\alpha_ \ldots i_>(x),\label
$$
где функции $\alpha_ \ldots i_>(x)$ бесконечно малые при $|\Delta x| \rightarrow 0$.

Так как $|\Delta x_| \leq |\Delta x|$, то $|\Delta x_> \ldots \Delta x_>| \leq |\Delta x|^$. Следовательно,
$$
\sum_ = 1>^ \ldots \sum_ <\substack= 1>>^ \alpha_ \ldots i_>(x) \Delta x_> \ldots \Delta x_> = o(|\Delta x|^)\label
$$
при $|\Delta x| \rightarrow 0$.Подставляя выражения \eqref и \eqref в формулу \eqref, получаем
$$
r_(x) = \frac<1> d^ f(x^<0>+\theta \Delta x) = \frac<1> \sum_ = 1>^ \ldots \sum_ <\substack= 1>>^ \frac <\partial^f(x^<0>)><\partial x_> \ldots \partial x_>> \Delta x_> \ldots \Delta x_> +\\+ \frac<1> \sum_ = 1>^ \ldots \sum_ <\substack= 1>>^ \alpha_ \ldots i_>(x) \Delta x_> \ldots \Delta x_> = \frac<1> d^ f(x^<0>)+o(|\Delta x|^)\label
$$
при $|\Delta x| \rightarrow 0$.

Подставляя выражение \eqref для $r_(x)$ в формулу \eqref, получаем формулу \eqref. $\bullet$

Источник