Обзор современных программ конечно-элементного анализа
На современном этапе развития науки и техники уже сложно представить проектирование изделий и конструкций без САПР. Наиболее ответственную роль среди всего многообразия CAD/CAM/CAE-программ играют пакеты конечно-элементного анализа. Круг решаемых ими задач охватывает почти все сферы инженерных расчетов: прочность, колебания, устойчивость, динамика, акустика, гидродинамика, аэродинамика и т.д. Представить полный список специализаций конечно-элементных программ, как и полный список всех пакетов программ конечно-элементного анализа (FEA-пакетов), фактически нереально. Однако провести краткий обзор наиболее распространенных конечно-элементных программ не только возможно, но и необходимо. У пользователей (или потенциальных пользователей) FEA-пакетов зачастую складывается мнение о превосходстве одного пакета над другим, сформированное в большей степени отсутствием информации о конкурирующих программных продуктах. Большую роль в этом играет то обстоятельство, что в большинстве технических вузов, официально использующих только один из пакетов, даже и не рассматриваются возможности других. Возникают необоснованные мифы о преимуществах и областях применения этих систем.
Бесспорно, лидером на рынке FEA-программ оказывается пакет ANSYS. Об этом говорит и количество легальных пользователей (более миллиона), и заявленные большие возможности, и компании, использующие данный пакет, а также немалая цена (обычно ассоциируемая с высоким качеством) да и самые высокие требования к оборудованию (для версии 5.5.1 рекомендуется компьютер с 256 Мбайт оперативной и 96 Мбайт видеопамяти). Более детальное описание пакета ANSYS можно найти на официальном сайте компании ANSYS — http://www.ansys.com или (русский, сокращенный вариант) на сайте российского распространителя (компании CAD-FEM-Russia) — http://www.cadfem.ru. Реальным достоинством этой системы является наиболее полная документация и система помощи, что позволяет, имея хорошие базовые (например, по механике) знания, использовать программу без обращения в службу поддержки пользователей. Обилие конечных элементов (более 100) впечатляет, но вызывает сомнение в их необходимости. Так, например, автору статьи легко и быстро удалось доказать активным участникам списка рассылки xANSYS бесполезность конечных элементов «Сэндвич» (в ANSYS — Shell91), используемых большинством квалифицированных пользователей неправильно. Посмотреть архив подписки можно по адресу onelist.com, подписаться — отправив e-mail (без заголовка и сообщения) по адресу xansys-subscribe@onelist.com. Активность (около 15 сообщений в сутки) независимого от фирмы ANSYS списка рассылки обусловлена отсутствием реальной поддержки фирмой своих пользователей.
В большинстве случаев на обращения по адресам support@ansys.com и info@ansys.com за помощью следуют необоснованные или бесполезные ответы, к примеру: «купите новую версию», или «пройдите наши фирменные курсы», или «в вашей версии не предусмотрена эта возможность…». Интерфейс программы впечатляет (но только пользователей, работавших ранее с конечно-элементными программами), в целом значительно уступая (в простоте, удобстве, логичности использования) универсальному интерфейсу под более чем 60 различных программ — FEMAP (разработчик Enterprise Software Products).
Сравниться с ANSYS (включая все его модификации в других пакетах) по количеству установок или легальных пользователей может только группа конечно-элементных программ с торговой маркой NASTRAN (официально марка принадлежит NASA (Cosmic)). Эту марку имеют такие наиболее распространенные пакеты: MSC/NASTRAN (компания MacNeal-Schwendler Corporation) и UAI/NASTRAN (компания Universal Analytics). Менее распространены NE/NASTRAN (компания Noran Engineering) и ME/NASTRAN (компания MacroIndustries). В России официальным распространением и поддержкой пакета UAI/NASTRAN занимается фирма TESIS, а поддержкой пакета MSC/NASTRAN — российское представительство компании MacNeal-Schwendler Corporation. Несмотря на значительно более низкую цену, реальные возможности пакетов фирм UAI, MSC, NE ни в чем не уступают пакету ANSYS, а иногда и превосходят в развитии и возможностях. Например, в течение более 5 лет в пакетах этих фирм доступен «предобусловленный метод сопряженных градиентов Холесского» (в ANSYS не представленный до 1999 года) как наиболее точный и быстрый для решения матриц высокого ранга. Уступают системе ANSYS пакеты NASTRAN, пожалуй, только ограниченным количеством поддерживаемых компьютерных платформ и операционных систем. Однако и этот недостаток оборачивается преимуществом, если учесть, что FEMAP-оболочки, используемые этими пакетами, очень удачно интегрированы в системы Windows 95/98/NT (что для российского пользователя наиболее актуально), а сами пакеты почти не требовательны к системным ресурсам. Например, для одной из последних версий MSC/NASTRAN v70.5 минимально необходим процессор 486DX, 16 Мбайт оперативной памяти и операционная система Windows 95. Согласитесь, что приученные к запросам продвинутого текстового редактора от фирмы Microsoft — Microsoft Word российские пользователи невольно засомневаются в возможностях подобного пакета. А зря!
Реальные независимые тесты всех рассмотренных программ можно найти на сервере http://www.nafems.com, однако особого различия как в скорости, так и в точности расчетов вы не обнаружите. Одно из исключений — очень медленный генератор сеток Algor. По остальным параметрам различие всех программ колеблется в диапазоне 10%. Ранее (до версии 5.5.x) ANSYS отставал в скорости расчета больших систем (более 100 000 уравнений) от остальных FEA-программ на 15% и более. Отсутствие значительного различия в быстродействии и точности FEA-программ объясняется использованием стандартных и широко известных алгоритмов решения задач методом конечных элементов. Математический аппарат, используемый в этих пакетах, также одинаков и широко известен. Ожидать принципиального прорыва того или иного пакета не приходится.
DANFE — программа для анализа усилий, деформаций, напряжений и смещений в конструкциях методом конечных элементов. Программа предоставляется как откомпилированная (готовая к работе на персональном компьютере), так и в виде текстов, готовых к компиляции на любой компьютерной системе, имеющей Fortran-компилятор.
По многим из параметров эта программа превосходит коммерческие. Повторим «изюминки»: доступен исходный текст, поддержка многопроцессорности (ставим под Linux на двухпроцессорной mainboard и рассчитываем конструкции быстрее, чем ANSYS на Sun-системах), наличие элементов с изменяемой во времени геометрией (эффекты самонапряжения, текучести, релаксации без внешних воздействий), солидный период (больше, чем ANSYS) апробации, авторитетный для всего мира производитель.
Другая программа — Mefisto, разработчик — лаборатория численного анализа университета Пьера и Марии Кюри (Париж, Франция), адрес Web-сервера — http://www.ann.jussieu.fr. Существуют версии для платформ: DEC, IBM, SUN, PC. Работает под UNIX-системами при наличии библиотеки X11 (для Linux и FreeBSD — стандартно поставляемая библиотека). Требования: 16 Мбайт оперативной памяти, 40 Мбайт дисковой памяти для выполняемых файлов, 128 Мбайт виртуальной (дисковой) памяти для временных файлов. Распространяется в двух вариантах:
Интересный факт, что текст программы (в последней редакции от июля 1999 года) содержит 267 319 строк (более километра распечатки на рулонной бумаге с плотностью 12 строк на дюйм), из которых 117 132 строки — комментарии! Имеется: «Руководство пользователя по пост/препроцессору», «Руководство пользователя «Механика», «Руководство пользователя «Теплодинамика» и т.д. Очень большие возможности программы проще проиллюстрировать в примерах пост/препроцессоров (рис. 1, 2).
Да, существуют универсальные, мощные, специализированные и бесплатные программы конечно-элементного анализа! Вы можете самостоятельно подобрать их (из нескольких десятков легкодоступных) с необходимыми для вас возможностями и законно использовать!
Приятной особенностью бесплатных программ является помощь разработчиков при проблемах в использовании, неприятной — отсутствие реакции на простые вопросы, описанные в документации. В коммерческих продуктах, наоборот, служба поддержки с удовольствием процитирует вам руководство пользователя, но промолчит в ответ на сложный вопрос! Другой важный момент: покупая коммерческую конечно-элементную программу, вы покупаете черный ящик, что там — неизвестно, вы можете уповать только на добросовестность разработчика. В бесплатных программах, наоборот, вы можете не только проверить весь текст программы, но и изменить некоторые участки.
Резонно возникает вопрос: а зачем тогда покупать дорогие пакеты? Наверное, из-за повышенной (гарантированной) надежности результата? Уточним, прочитав лицензионное соглашение одной (но характерное для всех) коммерческой конечно-элементной программы:
«. X) XXXXX warrants that the program, when delivered and installed, will conform to the specifications set forth in the current documentation. THIS IS THE ONLY WARRANTY OF ANY KIND, EXPRESSED OR IMPLIED, INCLUDING THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR PURPOSE THAT XXXXX MAKES.
X) Because this is an Evaluation System, we provide no maintenance or support. This system is to be used for evaluation purposes only. »
В свободном переводе на русский язык это звучит примерно так: «…х) продаем что есть, сделанное как умели и как знали.
х) никакой ответственности за результаты не несем, результаты расчетов только для ознакомления…»
Наверное, коммерческие программы более точно считают? Сомнительно, теория одна, алгоритмы одинаковые, более того, можно утверждать, что как коммерческие, так и бесплатные программы одинаково неточно считают! Как пояснение приведем несколько примеров (см. таблицу), сформированных на основе обнаруженных автором серии ошибок в теории метода конечных элементов. Отметим, что представленные примеры недоступны для правильного расчета в любых программах конечно-элементного анализа, как коммерческих, так и бесплатных.
Кроме аналитических методов правильность комментариев к первым двум примерам можно проверить, используя вместо силового воздействия управляемое перемещение. Например, для первого примера, указав перемещение узла по вертикали на 20 и как можно более мелкие шаги приращения воздействия, можно убедиться, что правильное положение, когда средний узел повернут вправо. Однако, введя данные в точном соответствии с задачей, легко убеждаемся, что все конечно-элементные программы выдают «левый» результат. Аналогично можно поступить и со вторым примером.
Необходимо уточнить, что в первом и втором примерах ответственной за все состояние конструкции является только одна проекция перемещения одного из узлов, то есть только одна переменная. Учитывая возможности современных компьютеров и позволив использовать большое количество подшагов итераций на каждом из шагов приращения нагрузки (то есть фактически сведя задачу к методу Монте-Карло), можно случайно попадать в зону правильного решения! Проверить случайность угадывания правильного положения достаточно легко: необходимо в файле задачи скопировать конструкцию на некоторое расстояние и изменить величину силы, например для первой задачи нарисовать две одинаковые конструкции, но для одной использовать силу 80, а для другой 180.
Представленные задачи, являясь с точки зрения теории надежности упорядоченной выборкой, свидетельствуют об очень близкой к 100% надежности получения неправильного результата во всех программах конечно-элементного анализа. Возможность случайного попадания в правильный результат компенсируется возможностью комбинации задач. Например, решив правильно только первую задачу, можно утверждать, что с вероятностью 50% правильно решаются задачи из трех элементов. Без верного решения всех четырех задач распространять определение вероятности правильного решения на любое количество элементов нельзя. Аналитические выкладки как правильности комментариев к задачам, так и определения надежности и вероятности не приводятся, так как предполагается, что статью читают как минимум студенты третьего курса.
В заключение хочется только посоветовать читателям больше думать и принимать самостоятельные, независимые решения. Помните, от большинства рассчитываемых конструкций и изделий зависит жизнь людей.
Нелинейный мир и инструменты для расчета сложных нелинейных задач методом конечных элементов
Привет, Хабр! В названии этой статьи есть словосочетание «нелинейный мир»… Думаю, что большинство читателей поняли смысл этого словосочетания, но я всё же расшифрую его.
Реальные системы можно рассматривать как линейные только в ограниченном диапазоне нагрузок. Реальный же мир вокруг нас нелинеен (рис. 1). Нелинейность есть нарушение принципа суперпозиции в некотором явлении (механической системе): результат действия суммы факторов не равен сумме результатов от отдельных факторов. Однако по разным причинам, в том числе в связи с отсутствием необходимых знаний, навыков моделирования, необходимого программного обеспечения, инженеры зачастую решают задачи только в линейных постановках. Даже когда линейный подход дает очень большие погрешности. Точное же моделирование поведения системы часто требует проведения нелинейного анализа.
Рис. 1
Введение
Пару месяцев назад я опубликовал статью «Просто о нелинейном анализе методом конечных элементов. На примере кронштейна». В ней я постарался доступно разъяснить минимальный объем терминов и теории, необходимой для осознанного проведения нелинейного статического анализа, подробно разобрал алгоритм решения простой нелинейной задачи. Повторяться не буду, напомню несколько основных положений – и приступим к обзору более сложных явлений, задач механики и инструментов, необходимых для решения этих нелинейных задач.
Линейные допущения часто справедливы, но сегодня при разработке изделий всё чаще необходимо проводить нелинейные расчеты. Чтобы сократить объем экспериментальной отработки, пользователи нуждаются в моделях более высокой точности: уточняются геометрические модели, увеличивается точность физических моделей. Это означает, что учитываются нелинейные эффекты, такие как контакты, большие деформации и свойства материала. Нелинейность задачи может быть обусловлена необходимостью учета истории нагружения конструкции – то есть разложение задачи на составляющие воздействия и последующее объединение результатов невозможны. Без учета этих эффектов решения могут оказаться неточными, что приведет к неверным выводам. Или же изделия могут быть спроектированы с очень большим запасом прочности, а потому станут слишком дорогостоящими.
Классическая физика и математика у нас одна, но в разных расчетных комплексах используются разные наборы алгоритмов и инструментов для решения задач методом конечных элементов. В этой статье я расскажу об инструментах, имеющихся в арсенале пре-постпроцессора Femap с решателем NX Nastran, за более чем 35 лет многократно доказавшим свои надежность, точность и скорость. Для решения самых сложных нелинейных задач, в том числе если необходимо учесть историю нагружения конструкции, подходит модуль многошаговых нелинейных решений Multistep Nonlinear (SOL401 / SOL402).
Контакты и применение сабкейсов
В рамках одного многошагового решения можно изменять условия контакта поверхностей с помощью сабкейсов. Сабкейсы – это отдельные решения, из которых можно сложить общее решение со сложной историей приложения нагрузок, изменения граничных условий. Например, при моделировании сборки можно добавлять или удалять контакты в определенной последовательности.
Трение может быть учтено в настройках контакта, а коэффициент трения – быть постоянным или изменяться в зависимости от скорости, температуры и времени. Детали, которые контактируют, обычно рассматриваются как деформируемые. Но если одна часть намного жестче другой, стоит рассматривать ее как жесткую, чтобы упростить задачу без существенных погрешностей. Это также позволяет применять принудительное перемещение твердого тела на жесткой части в качестве нагрузки.
На рис. 2 изображена модель, в которой резиновое уплотнительное кольцо задано гиперупругим материалом. Моделирование позволяет вычислить напряжения и перемещения в резиновом уплотнительном кольце, используемом для уплотнения крышки, надетой на цилиндр. В целях повышения эффективности модель строится с использованием осевой симметрии. Видимый круг – это поперечное сечение уплотнительного кольца. Размеры кольца уплотнителя в ненапряженном состоянии меньше диаметра цилиндра, поэтому начальное положение уплотнительного кольца показывает, что уплотнительное кольцо и цилиндр частично перекрываются. На первом этапе моделирования при определении контакта производится компенсация перекрытия, то есть уплотнительное кольцо растягивается радиально. Затем колпачок опускается и уплотнительное кольцо деформируется при соприкосновении со стенкой цилиндра. Таким образом образуется уплотнение.

Рис. 2
Геометрические несовершенства конечно-элементной сетки могут быть исправлены путем настройки допусков по зазорам и натягам или путем сглаживания граней. В случае возникновения трудностей со сходимостью есть множество вариантов решения этой проблемы. Например, опция «Нормальная регуляризация» полезна, когда условия контакта включают мягкие материалы, такие как резина. «Тангенциальная регуляризация» позволяет избежать разрывов в силах трения. Кроме того, локальная жесткость и демпфирование в контакте контролируются пользователем, что также может использоваться для улучшения сходимости. В постпроцессоре могут быть проанализированы следующие результаты: контактное давление, расстояние по нормали, скольжение, контактные силы.
Существует множество применений для контактов, включая болтовые соединения, имитацию падения и посадку с натягом. Моделировать болтовые соединения можно с помощью 1D конечных элементов (балки, стержни), 2D (плоские элементы) или 3D-элементов. Преднатяжение можно выполнять с помощью нескольких сабкейсов – например, если нужно смоделировать последовательность затяжки болтов. Сабкейсы преднатяжения могут быть реализованы не только первыми по счету, но и в любой последовательности. При анализе других сабкейсов вычисленные преднапряжения сохраняются, но фактическая нагрузка на болты может изменяться при дальнейшем приложении нагрузок. Пользователи могут анализировать нормальные, сдвиговые напряжения, моменты в болтах – на протяжении всего решения.
На рис. 3 изображена модель, позволяющая проанализировать следующую последовательность сборки/нагрузки/разгрузки: затяжка болта № 1, затяжка болта № 4, затяжка болта № 2, затяжка болта № 3, приложение эксплуатационной нагрузки, снятие нагрузки, снятие затяжки.
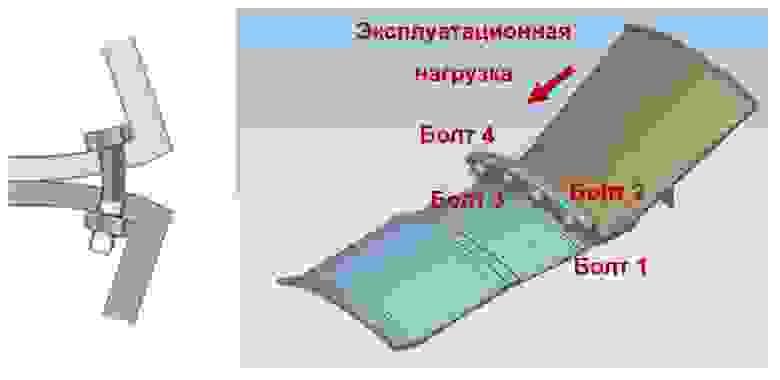
Рис. 3
Большие перемещения (деформации) и анализ после потери устойчивости
Большие линейные и угловые перемещения – это фундаментальные нелинейные эффекты (рис. 4). Они учитывают изменение положения нагрузки по мере деформации системы. Также существует эффект изменения жесткости изделия от нагрузки. Решение после потери устойчивости – это нелинейное решение с включенными эффектами больших деформаций.
Нагрузка вызывает потерю жесткости изделия, приводящую к последующим большим деформациям при небольших изменениях нагрузки. Существуют эффективные алгоритмы, позволяющие анализировать систему после превышения критической нагрузки потери устойчивости.

Рис. 4
Анализ после потери устойчивости – это особый тип статического сабкейса в Femap. В стандартном квазистатическом анализе нагрузки увеличиваются в соответствии с законом, определенным пользователем. Но некоторые изделия неустойчивы из-за их формы после достижения определенного уровня нагрузки. Такие изделия скачкообразно теряют жесткость в некотором диапазоне нагрузок. Для решения подобного рода задач следует использовать алгоритм «длины дуги» (arc length) – с его помощью решают задачи неустойчивого изгиба, потери устойчивости. Решение позволяет не только определить критическую нагрузку потери устойчивости на изгиб, но и проанализировать, как будет вести себя конструкция после того как она потеряет устойчивость. Вместо изменения нагрузок, основанных на временном приращении, алгоритм автоматически изменяет приращения нагрузки пропорционально перемещениям, а не времени.
Начальные несовершенства формы оказывают в задачах потери устойчивости большое влияние. Несовершенства формы могут быть учтены как искривления в геометрии/сетке, что можно использовать для учета несовершенств производственного процесса. Пользователь может моделировать места преднамеренного изгиба или моделировать повреждения, полученные в ходе эксплуатации.
Физическая нелинейность (нелинейность свойств материалов). Пластичность, гиперупругость, вязкость, ползучесть и композиты
В традиционном линейном анализе все материалы рассматриваются как линейные и упругие. Многошаговый нелинейный решатель Femap поддерживает нелинейные свойства совместно с изотропным, ортотропным, анизотропным поведением. Также поддерживаются еще несколько нелинейных моделей поведения материала, включая пластичность, гиперупругость, ползучесть и повреждение (damage). Пользователям, которым требуется задать уникальные свойства материалов, предоставлена возможность дополнительно добавлять собственные модели материалов.
Пластичные модели материалов с различными настройками доступны для моделирования. Пользователи могут задать кривую напряжений-деформаций как билинейную или полилинейную (рис. 5). Эффекты нагрузки/разгрузки могут быть описаны с помощью изотропных, кинематических или смешанных моделей упрочнения. Кривые напряжений-деформаций также могут быть дополнены температурной зависимостью. Таким образом материалы, зависимость свойств которых от температуры необходимо учесть при решении задачи, могут быть описаны адекватно.

Рис. 5
Гиперупругие материалы благодаря своим свойствам широко используются в различных отраслях. Они не зависят от скорости деформации. К таким материалам относятся резина, пена, биологические и полимерные материалы. Они поддерживают очень большие деформации (более 600%), практически несжимаемы, а также для них могут быть заданы температурные зависимости. Доступны стандартные модели материалов Муни-Ривлина (Mooney-Rivlin), Огдена (Ogden) с эффектом Муллинса (Mullins) и модели пенопласта. На рис. 6 изображена модель кожуха рукоятки переключения передач. Материал кожуха задан как гиперупругий резиновый материал с использованием модели Муни-Ривлина. Поверхности кожуха настроены для самоконтакта.

Рис. 6
Вязкоупругие материалы – это упругие материалы, обладающие способностью рассеивания механической энергии из-за влияния вязкости.
Эластичные материалы, такие как резина, растягиваются мгновенно и быстро возвращаются в исходное состояние после снятия нагрузки. Вязкость (внутреннее трение) – это свойство тела оказывать сопротивление перемещению одной его части относительно другой. Femap поддерживает вязкоупругие материалы с формулировками серий Кельвина и Прони. Модель Кельвина отражает явление упругого последействия, которое представляет собой изменение упругой деформации во времени, когда она или постоянно нарастает до некоторого предела после приложения нагрузки, или постепенно уменьшается после ее снятия (рис. 7). Когда снимается напряжение, материал постепенно расслабляется до недеформированной стадии. Модель Кельвина применяется для органических полимеров, резины, дерева при невысокой нагрузке.

Рис. 7
Деформации типа ползучести происходят с течением времени без какого-либо изменения нагрузки. Деформация при ползучести, как и при пластичности, является необратимой (неупругой), поведение материала при ползучести несжимаемое.
Многие материалы, особенно в условиях высокой температуры, могут испытывать деформации типа ползучести. Femap использует стандартную модель ползучести Бейли-Нортона и позволяет задавать температурные зависимости для определяющих коэффициентов.
В большинстве материалов при действии постоянной нагрузки выделяют три стадии ползучести (рис. 8). На первой стадии скорость деформации уменьшается со временем. Это явление наблюдается в течение короткого периода времени. Вторая стадия, более длительная, характеризуется постоянным значением скорости деформации. На третьей стадии скорость деформации быстро увеличивается вплоть до полного разрушения материала (разрыва образца).
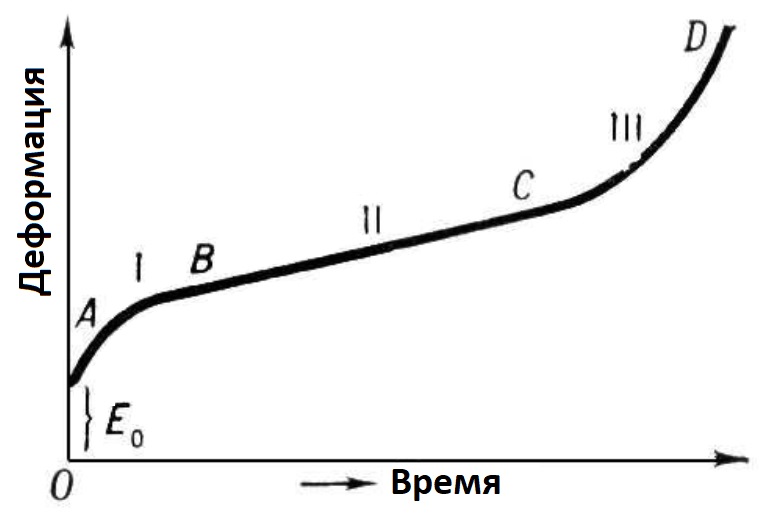
Рис. 8
Многошаговый нелинейный решатель Femap может моделировать нелинейное поведение композиционных материалов в результате внутрислоевого или межслоевого разрушения (рис. 9).
В случае внутрислоевого разрушения отдельные слои ослабевают и теряют жесткость при превышении определенного уровня нагрузки. Решатель отслеживает жесткость каждого слоя в изделии и обновляет жесткость элемента по мере того как слои становятся более поврежденными. В крайнем случае может произойти полная потеря жесткости в элементе. Внутрислоевые разрушения (для однонаправленного или тканого слоя) бывают различных типов: разрушение волокон, разрушение матрицы, разрушение связей между матрицей и волокнами.
При межслоевом разрушении связь между слоями изделия может ослабнуть и потерять жесткость. Femap использует связующие элементы для моделирования такого поведения. Моделирование показывает области, где связь теряется и слои могут отделяться.
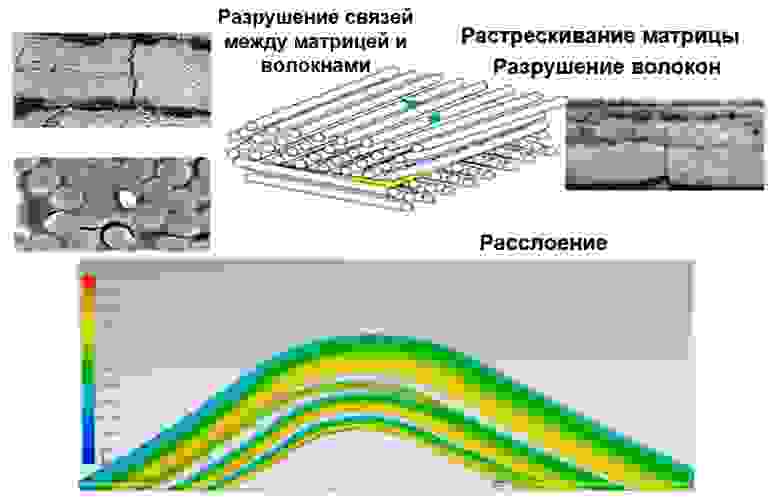
Рис. 9
Учет истории нагружения. Многошаговые решения с применением сабкейсов
Состояние конструкции в некоторых случаях зависит от последовательности приложения нагрузок, то есть нелинейность задачи может быть обусловлена необходимостью учета истории нагружения конструкции. Есть задачи, в которых достаточно учесть исходное напряженно-деформированное состояние (часто для нелинейностей, связанных с поведением материала). Но иногда бывает необходимо учесть сложную историю нагружения, состоящую из нескольких сабкейсов с изменяющимися силовыми факторами и граничными условиями. Граничные условия могут меняться при изменении площадок контакта.
Важной особенностью многошагового нелинейного решателя Femap является то, что он может поддерживать несколько сабкейсов и выполнять различные решения – такие как статические, динамические, модальные в отдельных сабкейсах в рамках одного решения. В дополнение к изменению типа анализа в сабкейсах также можно изменять настройки параметров и граничные условия. Это открывает пользователям большие возможности настройки решений. Вот типовой сценарий с использованием сабкейсов: каждый сабкейс начинается с условий, в которых закончился предыдущий сабкейс. Такой сабкейс называется последовательным. Но пользователь также может начать решение снова и не в последовательном сабкейсе.
На рис. 10 показан пример моделирования трех компонентов авиационного двигателя: два фланца и ступица соединены болтами в несколько этапов. Для эффективного решения используется симметричный сектор модели. На первом этапе анализируются отклонения от пресс-формы для одного фланца и ступицы. На втором два болта затягиваются, чтобы соединить фланец и ступицу. На третьем рассматривается запрессовка второго фланца. На четвертом затягиваются еще два болта, чтобы соединить второй фланец и ступицу. Затем, на пятом этапе, анализируется нагрузка от высокоскоростного вращения полностью соединенных деталей. Последним шагом является модальный анализ – он используется для прогнозирования напряжений от вибрации. Этот полный набор из шести шагов может быть выполнен в рамках одного анализа, что позволяет получить богатый набор данных для понимания напряженно-деформированного состояния двигателя.

Рис. 10
В дополнение к статическим сабкейсам поддерживаются динамические (transient). Этот тип сабкейса может начинать решение или следовать за статическими сабкейсами (рис. 11). При запуске решения могут быть применены начальные условия в форме перемещений или скорости. Например, для моделирования падения рационально начинать решение с точки непосредственно перед ударом и задавать начальную скорость, равную скорости удара. Если динамический анализ следует за статическим или другим динамическим анализом, то отклонения, скорости, ускорения в начале сабкейса будут такими же, как в конце предыдущего сабкейса.
В динамическом сабкейсе сгенерированные силы инерции, демпфирование, матрица жесткости и силы уравновешены приложенными нагрузками. Силы инерции можно отключить при анализе переходных процессов. Это очень полезно для ускорения решения и перехода к стационарному состоянию.
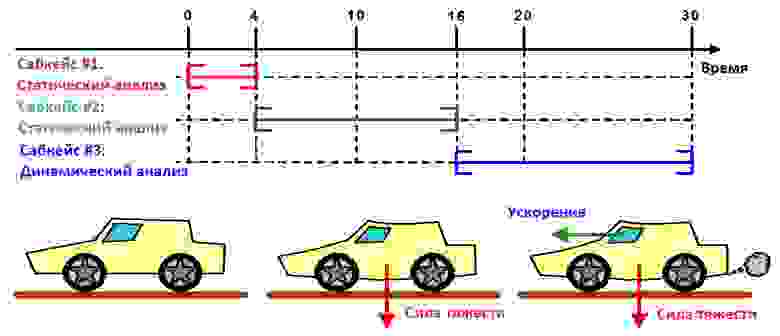
Рис. 11
Динамический анализ и моделирование кинематических связей
Моделирование падения часто выполняется для электронных приборов, чтобы понять, насколько хорошо они переживут столкновение с землей. На рис. 12 отображен ударный процесс, возникающий при падении тепловизионной камеры. Материал корпуса из поликарбоната моделируется как упругопластичный материал, а внутренняя печатная плата и электронные компоненты – как линейно-упругие материалы. Динамический анализ начинается с точки соприкосновения тепловизора с землей. Камере задается начальная скорость, соответствующая высоте, с которой она была сброшена (в данном случае это высота 1 метр). Камера быстро соприкасается с землей и отскакивает. Анализируются напряжения и деформации корпуса и бортов.

Рис. 12
Femap поддерживает применение кинематических связей для соединения различных частей сборки. Поддерживаются основные типы шарниров, такие как цилиндрические, сферические шарниры, жесткие и гибкие направляющие.
На рис. 13 изображен процесс развертывания солнечных панелей спутника, соединенных посредством цилиндрического шарнира. С помощью данной модели можно оценить вибрации и определить уровень напряжений.

Рис. 13
Заключение
Главными критериями качества для оценки расчетной модели и полученных результатов всегда были и будут сравнение с натурными экспериментами и аналитическими решениями. Нелинейные модели не являются исключением из правил. Разработчики Femap из компании Siemens проверяют нелинейные формулировки с помощью тестов NAFEMS (Международная ассоциация инженерного моделирования и анализа) и аналитических решений.
В дополнение к проверке формулировок, алгоритмы регулярно тестируются с помощью большой библиотеки тестовых моделей, чтобы избежать появления ошибок по мере добавления улучшений и расширений.
Однако перед каждым инженером каждый раз встает вопрос адекватности принятых допущений, правильного использования имеющихся программных инструментов и многокритериальной оценки полученных результатов.
В данной статье предложен обзор актуальных нелинейных задач и инструментов для их решения. Безусловно, этой информации недостаточно, чтобы на практике приступить к решению вышеобозначенных задач. Поэтому приглашаю вас на бесплатный вебинар «Femap и возможности модуля многошаговых нелинейных решений Multistep Nonlinear», который состоится 19 ноября 2020 года в 12:00. Во второй половине вебинара я решу задачу растяжения металлического образца с учетом пластичности и изотропного упрочнения материала.
Филипп Титаренко,
продакт-менеджер по направлению Femap
АО «Нанософт»
E-mail: titarenko@nanocad.ru
1. Femap с NX Nastran, Simcenter 3D Многошаговые нелинейные решатели: SOL401 / SOL402.Multistep Nonlinear (перевод Ф.В. Титаренко). Siemens.
2. NX Nastran Handbook of Nonlinear Analysis (Solutions 106 and 129). Siemens.

