Двоичное кодирование
Преобразование информации из непрерывной формы в дискретную
Для решения своих задач человеку часто приходится преобразовывать имеющуюся информацию из одной формы представления в другую. Например, при чтении вслух происходит преобразование информации из дискретной (текстовой) формы в непрерывную (звук). Во время диктанта на уроке русского языка, наоборот, происходит преобразование информации из непрерывной формы (голос учителя) в дискретную (записи учеников).
Информация, представленная в дискретной форме, значительно проще для передачи, хранения или автоматической обработки. Поэтому в компьютерной технике большое внимание уделяется методам преобразования информации из непрерывной формы в дискретную.
Дискретизация информации — процесс преобразования информации из непрерывной формы представления в дискретную.
Двоичноекодирование
В общем случае, чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка. Таких языков тысячи. Каждый язык имеет свой алфавит.
Алфавит — конечный набор отличных друг от друга символов (знаков), используемых для представления информации. Мощность алфавита — это количество входящих в него символов (знаков).
Алфавит, содержащий два символа, называется двоичным алфавитом (рис. 1.11). Представление информации с помощью двоичного алфавита называют двоичным кодированием. Закодировав таким способом информацию, мы получим её двоичный код.
Рассмотрим в качестве символов двоичного алфавита цифры 0 и 1.
Покажем, что любой алфавит можно заменить двоичным алфавитом. Прежде всего, присвоим каждому символу рассматриваемого алфавита порядковый номер. Номер представим с помощью двоичного алфавита. Полученный двоичный код будем считать кодом исходного символа (рис. 1.12).
Порядковому номеру каждого символа исходного алфавита будет поставлена в соответствие цепочка (последовательность) из нескольких двоичных символов.
Правило получения двоичных кодов для символов алфавита мощностью больше двух можно представить схемой на рис. 1.13.
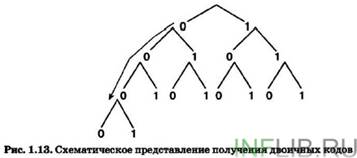
Двоичные символы (0,1) здесь берутся в заданном алфавитном порядке и размещаются слева направо. Двоичные коды (цепочки символов) читаются сверху вниз. Все цепочки (кодовые комбинации) из двух двоичных символов позволяют представить четыре различных символа произвольного алфавита:
| Порядковый номер символа |
| Двухразрядный двоичный код |
Цепочки из трёх двоичных символов получаются дополнением двухразрядных двоичных кодов справа символом 0 или 1. В итоге кодовых комбинаций из трёх двоичных символов получается 8 — вдвое больше, чем из двух двоичных символов:
| Порядковый номер символа |
| Трёхразрядный двоичный код |
Соответственно, четырёхразрядйый двоичный код позволяет получить 16 кодовых комбинаций, пятиразрядный — 32, шестиразрядный — 64 и т. д. Длину двоичной цепочки — количество символов в двоичном коде — называют разрядностью двоичного кода.
| Разрядность двоичного кода |
| Количество кодовых комбинаций |
Обратите внимание, что:
4 = 2 * 2,
8 = 2 * 2 * 2,
16 = 2 * 2 * 2 * 2,
И т. д.
Дата добавления: 2015-11-20 ; просмотров: 1952 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Информатика. 7 класс
Конспект урока
Кодирование информации. Двоичный код
Перечень вопросов, рассматриваемых в теме:
Дискретизация информации – процесс преобразования информации из непрерывной формы представления в дискретную. Чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка.
Алфавит языка – конечный набор отличных друг от друга символов, используемых для представления информации. Мощность алфавита – это количество входящих в него символов.
Алфавит, содержащий два символа, называется двоичным алфавитом. Представление информации с помощью двоичного алфавита называют двоичным кодированием. Двоичное кодирование универсально, так как с его помощью может быть представлена любая информация.
1. Босова Л. Л. Информатика: 7 класс. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2017. – 226 с.
Теоретический материал для самостоятельного изучения
Для решения своих задач человеку часто приходится преобразовывать имеющуюся информацию из одной формы представления в другую. Например, при чтении вслух происходит преобразование информации из дискретной (текстовой) формы в непрерывную (звук). Во время диктанта на уроке русского языка, наоборот, происходит преобразование информации из непрерывной формы (голос учителя) в дискретную (записи учеников).
Информация, представленная в дискретной форме, значительно проще для передачи, хранения или автоматической обработки. Поэтому в компьютерной технике большое внимание уделяется методам преобразования информации из непрерывной формы в дискретную.
Дискретизация информации – процесс преобразования информации из непрерывной формы представления в дискретную.
Рассмотрим суть процесса дискретизации информации на примере.
На метеорологических станциях имеются самопишущие приборы для непрерывной записи атмосферного давления. Результатом их работы являются барограммы – кривые, показывающие, как изменялось давление в течение длительных промежутков времени. Одна из таких кривых, вычерченная прибором в течение семи часов проведения наблюдений, показана на рисунке 1.
На основании полученной информации можно построить таблицу, содержащую показания прибора в начале измерений и на конец каждого часа наблюдений.
Полученная таблица даёт не совсем полную картину того, как изменялось давление за время наблюдений: например, не указано самое большое значение давления, имевшее место в течение четвёртого часа наблюдений. Но если занести в таблицу значения давления, наблюдаемые каждые полчаса или 15 минут, то новая таблица будет давать более полное представление о том, как изменялось давление.
Таким образом, информацию, представленную в непрерывной форме (барограмму, кривую), мы с некоторой потерей точности преобразовали в дискретную форму (таблицу).
В дальнейшем вы познакомитесь со способами дискретного представления звуковой и графической информации.
В общем случае, чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка. Таких языков тысячи. Каждый язык имеет свой алфавит.
Алфавит – конечный набор отличных друг от друга символов (знаков), используемых для представления информации. Мощность алфавита – это количество входящих в него символов (знаков).
Алфавит, содержащий два символа, называется двоичным алфавитом (рис. 3). Представление информации с помощью двоичного алфавита называют двоичным кодированием. Закодировав таким способом информацию, мы получим её двоичный код.
Рассмотрим в качестве символов двоичного алфавита цифры 0 и 1. Покажем, что любой алфавит можно заменить двоичным алфавитом. Прежде всего, присвоим каждому символу рассматриваемого алфавита порядковый номер. Номер представим с помощью двоичного алфавита. Полученный двоичный код будем считать кодом исходного символа.
Если мощность исходного алфавита больше двух, то для кодирования символа этого алфавита потребуется не один, а несколько двоичных символов. Другими словами, порядковому номеру каждого символа исходного алфавита будет поставлена в соответствие цепочка (последовательность) из нескольких двоичных символов. Правило получения двоичных кодов для символов алфавита мощностью больше двух можно представить схемой на рисунке.
Двоичные символы (0,1) здесь берутся в заданном алфавитном порядке и размещаются слева направо. Двоичные коды (цепочки символов) читаются сверху вниз. Все цепочки (кодовые комбинации) из двух двоичных символов позволяют представить четыре различных символа произвольного алфавита:
Цепочки из трёх двоичных символов получаются дополнением двухразрядных двоичных кодов справа символом 0 или 1. В итоге кодовых комбинаций из трёх двоичных символов получается 8 – вдвое больше, чем из двух двоичных символов:
Соответственно, четырёхразрядный двоичный код позволяет получить 16 кодовых комбинаций, пятиразрядный – 32, шестиразрядный – 64 и т. д.
Длину двоичной цепочки – количество символов в двоичном коде – называют разрядностью двоичного кода.
Обратите внимание, что:
32 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 и т. д.
Здесь количество кодовых комбинаций представляет собой произведение некоторого количества одинаковых множителей, равного разрядности двоичного кода.
Если количество кодовых комбинаций обозначить буквой N, а разрядность двоичного кода – буквой i, то выявленная закономерность в общем виде будет записана так:
В математике такие произведения записывают в виде:
Запись 2 i читают так: «2 в i-й степени».
Задача. Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию. Двоичный код какой разрядности потребуется, если алфавит, используемый племенем Мульти, содержит 16 символов? Выпишите все кодовые комбинации.
Чтобы выписать все кодовые комбинации из четырёх 0 и 1, воспользуемся схемой на рис. 1.13: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.
Универсальность двоичного кодирования
В начале нашей беседы вы узнали, что информация, представленная в непрерывной форме, может быть выражена с помощью символов некоторого естественного или формального языка. В свою очередь, символы произвольного алфавита могут быть преобразованы в двоичный код. Таким образом, с помощью двоичного кода может быть представлена любая информация на естественных и формальных языках, а также изображения и звуки (рис. 6). Это и означает универсальность двоичного кодирования.
Двоичные коды широко используются в компьютерной технике, требуя только двух состояний электронной схемы – «включено» (это соответствует цифре 1) и «выключено» (это соответствует цифре 0).
Простота технической реализации – главное достоинство двоичного кодирования. Недостаток двоичного кодирования – большая длина получаемого кода.
Равномерные и неравномерные коды
Различают равномерные и неравномерные коды. Равномерные коды в кодовых комбинациях содержат одинаковое число символов, неравномерные – разное.
Выше мы рассмотрели равномерные двоичные коды.
Примером неравномерного кода может служить азбука Морзе, в которой для каждой буквы и цифры определена последовательность коротких и длинных сигналов. Так, букве Е соответствует короткий сигнал («точка»), а букве Ш – четыре длинных сигнала (четыре «тире»). Неравномерное кодирование позволяет повысить скорость передачи сообщений за счёт того, что наиболее часто встречающиеся в передаваемой информации символы имеют самые короткие кодовые комбинации.
Разбор решения заданий тренировочного модуля
№1.Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Переведите десятичное число 273 в двоичную систему счисления.
Воспользуемся алгоритмом перевода целых чисел из системы с основанием p в систему с основанием q:
1. Основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления.
2. Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, меньшее делителя.
3. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
4. Составить число в новой системе счисления, записывая его, начиная с последнего остатка.
Ответ: 27310= 100010001.
№2. Тип задания: единичный / множественный выбор.
Четыре буквы латинского алфавита закодированы кодами различной длины:
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 1.5. Двоичное кодирование
Информатика. 7 класса. Босова Л.Л. Оглавление
1.5.1. Преобразование информации из непрерывной формы в дискретную
Для решения своих задач человеку часто приходится преобразовывать имеющуюся информацию из одной формы представления в другую. Например, при чтении вслух происходит преобразование информации из дискретной (текстовой) формы в непрерывную (звук). Во время диктанта на уроке русского языка, наоборот, происходит преобразование информации из непрерывной формы (голос учителя) в дискретную (записи учеников).
Информация, представленная в дискретной форме, значительно проще для передачи, хранения или автоматической обработки. Поэтому в компьютерной технике большое внимание уделяется методам преобразования информации из непрерывной формы в дискретную.
Дискретизация информации — процесс преобразования информации из непрерывной формы представления в дискретную.
Рассмотрим суть процесса дискретизации информации на примере.
На метеорологических станциях имеются самопишущие приборы для непрерывной записи атмосферного давления. Результатом их работы являются барограммы — кривые, показывающие, как изменялось давление в течение длительных промежутков времени. Одна из таких кривых, вычерченная прибором в течение семи часов проведения наблюдений, показана на рис. 1.9.
На основании полученной информации можно построить таблицу, содержащую показания прибора в начале измерений и на конец каждого часа наблюдений (рис. 1.10).
Полученная таблица даёт не совсем полную картину того, как изменялось давление за время наблюдений: например, не указано самое большое значение давления, имевшее место в течение четвёртого часа наблюдений. Но если занести в таблицу значения давления, наблюдаемые каждые полчаса или 15 минут, то новая таблица будет давать более полное представление о том, как изменялось давление.
Таким образом, информацию, представленную в непрерывной форме (барограмму, кривую), мы с некоторой потерей точности преобразовали в дискретную форму (таблицу).
В дальнейшем вы познакомитесь со способами дискретного представления звуковой и графической информации.
1.5.2. Двоичное кодирование
В общем случае, чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка. Таких языков тысячи. Каждый язык имеет свой алфавит.
Алфавит — конечный набор отличных друг от друга символов (знаков), используемых для представления информации. Мощность алфавита — это количество входящих в него символов (знаков).
Алфавит, содержащий два символа, называется двоичным алфавитом (рис. 1.11). Представление информации с помощью двоичного алфавита называют двоичным кодированием. Закодировав таким способом информацию, мы получим её двоичный код.
Рассмотрим в качестве символов двоичного алфавита цифры 0 и 1.
Покажем, что любой алфавит можно заменить двоичным алфавитом. Прежде всего, присвоим каждому символу рассматриваемого алфавита порядковый номер. Номер представим с помощью двоичного алфавита. Полученный двоичный код будем считать кодом исходного символа (рис. 1.12).
Если мощность исходного алфавита больше двух, то для кодирования символа этого алфавита потребуется не один, а несколько двоичных символов. Другими словами, порядковому номеру каждого символа исходного алфавита будет поставлена в соответствие цепочка (последовательность) из нескольких двоичных символов.
Правило получения двоичных кодов для символов алфавита мощностью больше двух можно представить схемой на рис. 1.13.
Двоичные символы (0,1) здесь берутся в заданном алфавитном порядке и размещаются слева направо. Двоичные коды (цепочки символов) читаются сверху вниз. Все цепочки (кодовые комбинации) из двух двоичных символов позволяют представить четыре различных символа произвольного алфавита:
Цепочки из трёх двоичных символов получаются дополнением двухразрядных двоичных кодов справа символом 0 или 1. В итоге кодовых комбинаций из трёх двоичных символов получается 8 — вдвое больше, чем из двух двоичных символов:
Соответственно, четырёхразрядный двоичный код позволяет получить 16 кодовых комбинаций, пятиразрядный — 32, шестиразрядный — 64 и т. д.
Длину двоичной цепочки — количество символов в двоичном коде — называют разрядностью двоичного кода.
Обратите внимание, что:
Здесь количество кодовых комбинаций представляет собой произведение некоторого количества одинаковых множителей, равного разрядности двоичного кода.
Если количество кодовых комбинаций обозначить буквой N, а разрядность двоичного кода — буквой i, то выявленная закономерность в общем виде будет записана так:
В математике такие произведения записывают в виде:
Запись 2 i читают так: «2 в i-й степени».
Задача. Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию. Двоичный код какой разрядности потребуется, если алфавит, используемый племенем Мульти, содержит 16 символов? Выпишите все кодовые комбинации.
Чтобы выписать все кодовые комбинации из четырёх 0 и 1, воспользуемся схемой на рис. 1.13: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.
На сайте http://sc.edu.ru/ размещена виртуальная лаборатория «Цифровые весы» (135009). С её помощью вы можете самостоятельно открыть метод разностей — ещё один способ получения двоичного кода целых десятичных чисел.
1.5.3. Универсальность двоичного кодирования
В начале этого параграфа вы узнали, что информация, представленная в непрерывной форме, может быть выражена с помощью символов некоторого естественного или формального языка. В свою очередь, символы произвольного алфавита могут быть преобразованы в двоичный код. Таким образом, с помощью двоичного кода может быть представлена любая информация на естественных и формальных языках, а также изображения и звуки (рис. 1.14). Это и означает универсальность двоичного кодирования.
Двоичные коды широко используются в компьютерной технике, требуя только двух состояний электронной схемы — «включено» (это соответствует цифре 1) и «выключено» (это соответствует цифре 0).
Простота технической реализации — главное достоинство двоичного кодирования. Недостаток двоичного кодирования — большая длина получаемого кода.
1.5.4. Равномерные и неравномерные коды
Различают равномерные и неравномерные коды. Равномерные коды в кодовых комбинациях содержат одинаковое число символов, неравномерные — разное.
Выше мы рассмотрели равномерные двоичные коды.
Примером неравномерного кода может служить азбука Морзе, в которой для каждой буквы и цифры определена последовательность коротких и длинных сигналов. Так, букве Е соответствует короткий сигнал («точка»), а букве Ш — четыре длинных сигнала (четыре «тире»). Неравномерное кодирование позволяет повысить скорость передачи сообщений за счёт того, что наиболее часто встречающиеся в передаваемой информации символы имеют самые короткие кодовые комбинации.
Самое главное.
Дискретизация информации — процесс преобразования информации из непрерывной формы представления в дискретную. Чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка.
Алфавит языка — конечный набор отличных друг от друга символов, используемых для представления информации. Мощность алфавита — это количество входящих в него символов.
Алфавит, содержащий два символа, называется двоичным алфавитом. Представление информации с помощью двоичного алфавита называют двоичным кодированием. Двоичное кодирование универсально, так как с его помощью может быть представлена любая информация.
Вопросы и задания.
1.Ознакомьтесь с материалом презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
Двоичная система счисления
Двоичный код — понятие, которое кажется сложным большинству людей. Однако на самом деле это одна из самых простых шифровальных систем в мире. Более того, мы сталкиваемся с ней ежедневно в обычной жизни.
Например, в наших компьютерах хранится самая различная информация — текстовые файлы, видеоролики, аудиозаписи и изображения. Но в виде картинок, текстов и мультимедийных файлов эту информацию видим только мы — а сам компьютер воспринимает и обрабатывает любые сведения в форме двоичного кода.
Двоичная система счисления — что это такое?
Двоичный, или, как еще его называют, бинарный код — шифр, состоящий всего из двух символов. Его можно сравнить с азбукой Морзе, где используются только тире и точки в разных комбинациях — морзянкой передают сколь угодно сложные сообщения.
Двоичный код чаще всего представлен нулем и единицей. Но это не обязательно — двоичного кода можно брать и любые другие обозначения, главное, чтобы эти символы были противоположными или взаимоисключающими по сути.
Что такое разрядность двоичного кода?
Одним из важных свойств двоичной системы является понятие разрядности — этим словом называют количество позиций, используемых в конкретном коде для составления комбинаций.
Смысл разрядного двоичного кода заключается в том, что одно и то же число в нем можно обозначить разными комбинациями символов — например, обозначения 0001, 001, 01 и 1 будут подразумевать одно и то же число «1». Читают разряды не так, как текст, а справа налево. Как правило, на практике код бывает 4, 8, 16, 32 и 64 разрядным — в зависимости от объема информации и специфики решаемой задачи.
У неопытного пользователя может возникнуть вопрос — какой смысл в двоичной системе, и не проще ли обходиться без нее? Однако когда речь идет о сложной вычислительной технике, то оперировать огромным множеством простейших элементов для нее удобнее, нежели обращаться с малочисленными, но сложными символами.