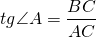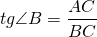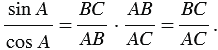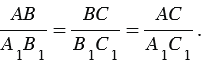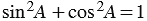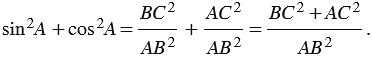Синус, косинус, тангенс в прямоугольном треугольнике
Гипотенузой называется та сторона треугольника, что лежит против угла в 90 градусов, две оставшиеся стороны называются катетами прямоугольного треугольника.
Подробнее про прямоугольный треугольник здесь.
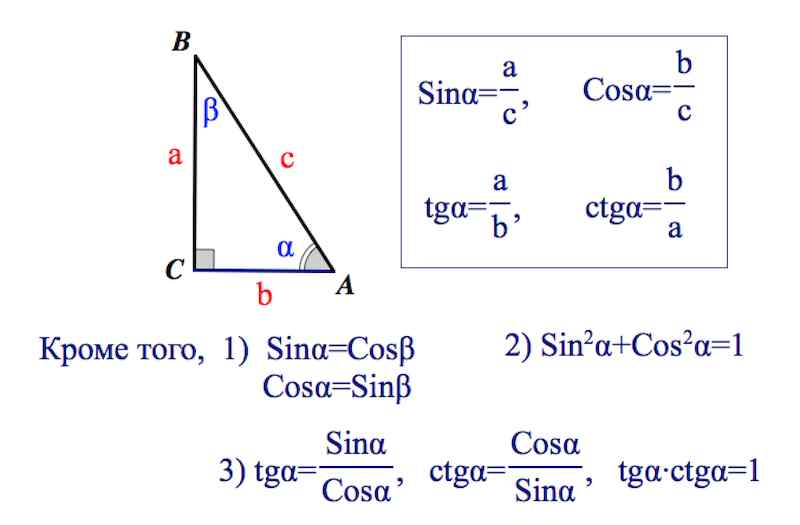
Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Котангенсом угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
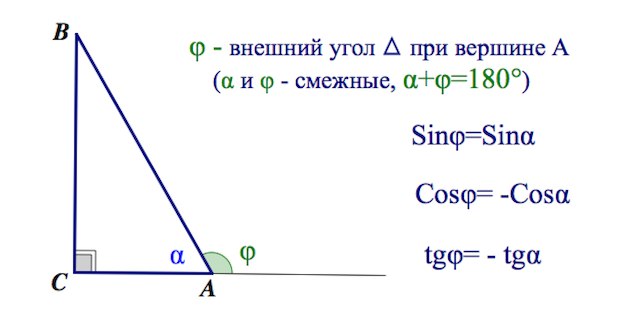
Бывает (и на ЕГЭ, ГИА), что приходится иметь дело с косинусами, синусами и тангенсами внешних углов треугольника. Формулы приведения позволяют увидеть, что есть еще и вот такая связь между смежными углами (помимо того, что их сумма равна 180):
Смотрите подборку задач на применение указанных соотношений в статье «Прямоугольный треугольник. Вычисление длин и углов» часть I, часть II.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Тангенс в прямоугольном треугольнике
Что такое тангенс в прямоугольном треугольнике? Как найти тангенс? От чего зависит значение тангенса?
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
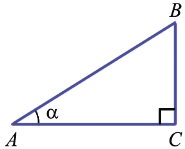
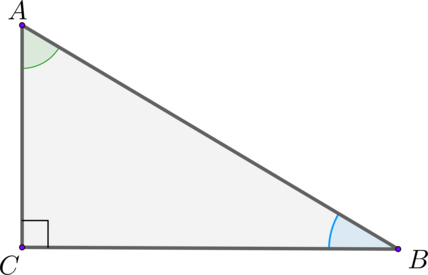
Например, для угла A треугольника ABC
Поэтому тангенс угла A в треугольнике ABC — это
Для угла B треугольника ABC
противолежащим является катет AC,
Соответственно, тангенс угла B в треугольнике ABC
равен отношению AC к BC:
Таким образом, тангенс острого угла прямоугольного треугольника — это некоторое число, получаемое при делении длины противолежащего катета на длину прилежащего катета.
Так как длины катетов — положительные числа, то и тангенс острого угла прямоугольного треугольника является положительным числом.
Тангенс угла треугольника зависит от величины угла, но не зависит от катетов (важно лишь их отношение).
Если в треугольнике изменить длины катетов, не меняя угол, то величина тангенса не изменится.
Синус, косинус и тангенс острого угла прямоугольного треугольника
(1)
(2)
(3)
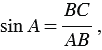
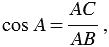
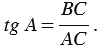
Из формул (1) и (2) получаем:
Сравнивая с формулой (3), находим:
(4)
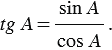
Получили, что тангенс угла равен отношению синуса к косинусу этого угла.
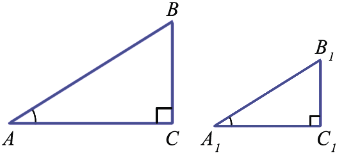
Докажем, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
Доказать: sin A = sin A1, cos A = cos A1, tg A = tg A1.
Доказательство:
Из этих равенств следует, что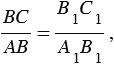 
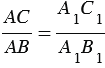
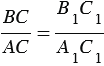
т.е. sin A = sin A1. Аналогично 
, т.е. cos A = cos A1, и 
, т.е. tg A = tg A1, что и требовалось доказать.
Мы получили, что синус, косинус и тангенс острого угла зависит только от величины этого угла.
Докажем основное тригонометрическое тождество:
Из формул (1) и (2) получаем
По теореме Пифагора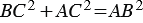 
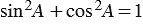
, поэтому 
.
Поделись с друзьями в социальных сетях:
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
Обратите внимание на основные соотношения для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
Давайте докажем некоторые из них.
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
| 0 | |
| 0 | |
| 0 | |
| 0 | − |
| − | 0 |
Обратите внимание на два красных прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Ты нашел то, что искал? Поделись с друзьями!
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача решается за четыре секунды.
Найдем по теореме Пифагора.
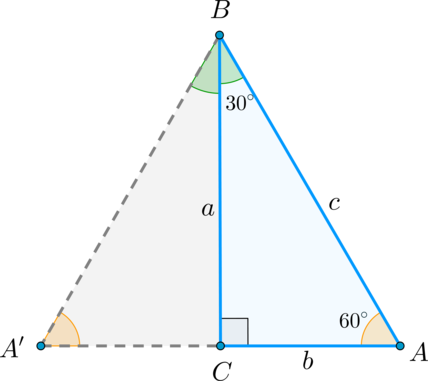
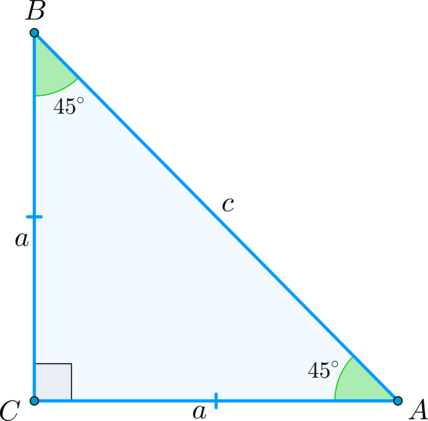
Треугольник с углами и — равнобедренный. В нем гипотенуза в раз больше катета.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Начальные сведения о синусе, косинусе, тангенсе и котангенсе
Определения
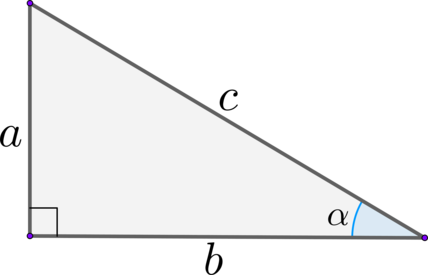
Синус острого угла в прямоугольном треугольнике – это отношение противолежащего к этому углу катета к гипотенузе: \(\sin \alpha=\dfrac ac\)
Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего к этому углу катета к гипотенузе: \(\cos \alpha=\dfrac bc\)
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего к этому углу катета к прилежащему катету: \(\mathrm
Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего к этому углу катета к противолежащему катету: \(\mathrm
Утверждение
Синусы, косинусы, тангенсы и котангенсы равных углов соответственно равны.
Теорема
Из определений синуса, косинуса, тангенса и котангенса вытекают следующие формулы:
Утверждение
В прямоугольном треугольнике \(ABC\) с прямым углом \(\angle C\) :
\(\sin \angle A=\cos \angle B\)
Доказательство
Утверждение следует непосредственно из определения синуса и косинуса острого угла в прямоугольном треугольнике.
Теорема
Для углов \(30^\circ, 45^\circ, 60^\circ\) верна следующая таблица:
\[<\large<\begin
Доказательство
Теперь по определению \(\sin \angle A=\sin 60^\circ =\dfrac ac=\dfrac<\sqrt3>2\)
Замечание
Для простоты запоминания таблицы можно записать ее в следующем виде:
Теорема
Справедливы следующие формулы приведения:
\[\begin
Пример
Учащиеся, которые готовятся к сдаче ЕГЭ по математике и при этом рассчитывают на получение конкурентных баллов по итогам его прохождения, непременно должны повторить теорию о синусе, косинусе, тангенсе и котангенсе. Как показывает практика, задания по данной тематике ежегодно встречаются в аттестационном испытании. Таким образом, если одним из ваших слабых мест являются формулы и теоремы синусов, косинусов, тангенсов и котангенсов, рекомендуем освежить в памяти базовую теорию. В этом вам поможет образовательный портал «Школково». В соответствующем разделе представлена теория о синусах, косинусах, тангенсах и котангенсах, которая позволит вам подготовиться к сдаче экзамена. Весь базовый материал составлен нашими специалистами на основе многолетнего опыта и представлен в максимально доступной форме. Ознакомившись с теорией, выпускник сможет грамотно объяснять решение задач ЕГЭ на синусы, косинусы, тангенсы и котангенсы. В этом состоит половина успеха при прохождении аттестационного испытания.
Для того чтобы учащиеся из Москвы или другого населенного пункта России, посетившие наш ресурс, смогли легко и качественно подготовиться к ЕГЭ, мы не только в понятной форме изложили теорию косинусов, синусов, тангенсов и котангенсов, но и подобрали соответствующие упражнения. Для каждого из них наши специалисты прописали подробный алгоритм решения и правильный ответ. Выполняя такие задачи при подготовке к ЕГЭ по математике, выпускники смогут лучше закрепить изученную теорию синусов и косинусов в треугольнике. Выбрать простые и более сложные упражнения вы можете в разделе «Каталог».
Изучив теорию о синусах, косинусах, тангенсах и котангенсах и попрактиковавшись в решении задач по данной теме при подготовке к ЕГЭ, учащиеся имеют возможность сохранить любое задание в «Избранное», чтобы при необходимости обсудить его с преподавателем.