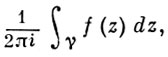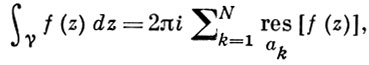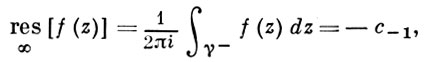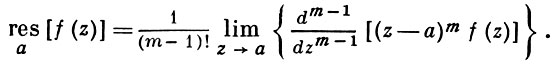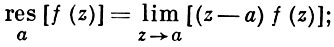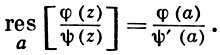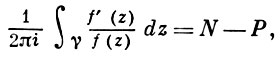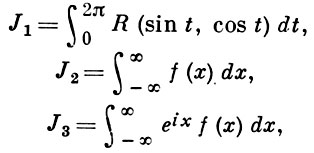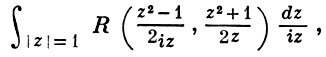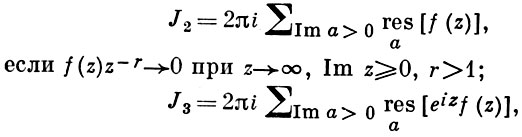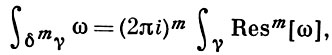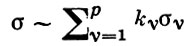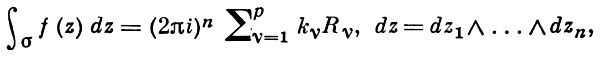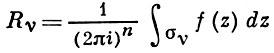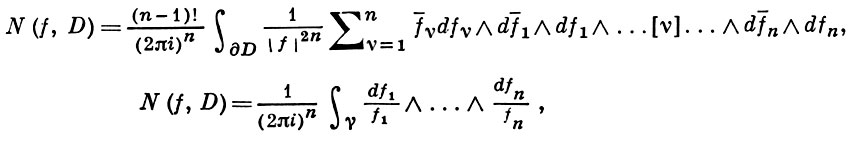Логарифмический вычет
Вы́чет в компле́ксном анализе — объект (число, форма или когомологический класс формы), характеризующий локальные свойства заданной функции или формы.
Содержание
Одномерный комплексный анализ [ | ]
Вычет функции [ | ]
Вычет в «бесконечности» [ | ]
Цикл интегрирования в этом определении ориентирован положительно, то есть против часовой стрелки.
Аналогично предыдущему случаю вычет в бесконечности имеет представление и в виде коэффициента лорановского разложения в окрестности бесконечно удалённой точки:
Вычет дифференциальной формы [ | ]
Логарифмические вычеты [ | ]
Понятие логарифмического вычета используется для доказательства теоремы Руше и основной теоремы алгебры.
Способы вычисления вычетов [ | ]
Согласно определению вычет может быть вычислен как контурный интеграл, однако в общем случае это довольно трудоёмко. Поэтому на практике пользуются, в основном, следствиями из определения.
Приложения теории вычетов [ | ]
В большинстве случаев теория вычетов применяется для вычисления разного рода интегральных выражений с помощью основной теоремы о вычетах. Часто полезной в данных случаях бывает лемма Жордана.
Вычисления определённых интегралов от тригонометрических функций [ | ]
Вычисление несобственных интегралов [ | ]
Для вычисления несобственных интегралов с применением теории вычетов используют следующие две леммы:
∫ − ∞ + ∞ f ( x ) d x = 2 π i ∑ k = 1 n R e s z = z k f ( z ) <\displaystyle \int \limits _<-\infty >^<+\infty >\!f(x)\,dx=2\pi i\sum _
∫ − ∞ + ∞ f ( x ) e i α x d x = 2 π i ∑ k = 1 n R e s z = z k f ( z ) e i α z <\displaystyle \int \limits _<-\infty >^<+\infty >\!f(x)e^
При этом интегралы в левых частях равенств не обязаны существовать и поэтому понимаются только лишь в смысле главного значения (по Коши).
ВЫЧЕТ
Вычет функции в бесконечно удаленной точке n = ∞ для функции f(z), однозначной и аналитической в окрестности этой точки, определяется формулой
При m = 1 (простой полюс) эта формула принимает вид
если f(z) = φ(z)/ψ(z), где φ(z) и ψ(z) регулярны в окрестности точки а, причем для φ(z) точка а есть простой нуль, то
Применение теоремы о В. к логарифмич. производной приводит к важной теореме о логарифмическом вычете: если функция f(z) мероморфна в односвязной области G, а простая замкнутая кривая γ лежит в G и не проходит через нули и полюсы функции f(z), то
В. применяются к вычислению нек-рых определенных интегралов от действительных функций, таких, напр., как
т. е. к вычислению В.;
если f(z) удовлетворяет условиям Жордана леммы.
Теория В. одного переменного разработана в основном О. Коши (A. Cauchy) в 1825-29. Ряд результатов, относящихся к обобщениям теории В. и ее приложениям, был получен Ш. Эрмитом (Ch. Hermite, теорема о сумме В. двоякопериодической функции), П. Лораном (P. Laurent), Ю. В. Сохоцким, Э. Линделёфом (Е. Lindelöf) и др.
Теория вычетов аналитических функций многих комплексных переменных базируется на интегральных теоремах Стокса и Коши-Пуанкаре, позволяющих заменять интеграл от замкнутой формы по одному циклу интегралом от этой формы по другому циклу, гомологичному первому. Начало теории В. функции многих переменных положил А. Пуанкаре [6], к-рый в 1887 впервые обобщил интегральную теорему Коши и понятие В. на функции двух комплексных переменных, показав, в частности, что интеграл от рациональной функции двух комплексных переменных по двумерному циклу, не проходящему через особенности подинтегральной функции, сводится к периодам абелевых интегралов, и применил двойные В. для обоснования двумерного аналога Лагранжа ряда.
— разложение σ по этой базе, то обобщение теоремы о В. имеет вид
Лит.: [1] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1, М., 1967; [2] Евграфов М. А., Аналитические функции, 2 изд., М., 1968; [3] Привалов И. И., Введение в теорию функций комплексного переменного, 11 изд., М., 1967; [4] Шабат Б. В., Введение в комплексный анализ, М., 1969; [5] Спрингер Д., Введение в теорию римановых поверхностей, пер. с англ., М., 1960; [6] Pоinсаré Н., «Acta math.», 1887, t. 9, 321-380; [7] Лере Ж., Дифференциальное и интегральное исчисления на комплексном аналитическом многообразии, пер. с франц., М., 1961; [8] Фукс Б. А., Введение в теорию аналитических функций многих переменных, М., 1962; [9] Южаков А. П., «Изв. ВУЗов. Матем.», 1964, № 5 (42), с. 149-61; [10] Griffits P. А., «Аnn. Math.», 1969, v. 90, № 3, р. 460-95; [11] Егорычев Г. П., Южаков А. П., «Сиб. матем. ж.», 1974, т. 15, № 5, 1049-60; [12] Южаков А. П., Элементы теории многомерных вычетов, Красноярск, 1975.
Теорема о логарифмическом вычете
Название работы: Теорема о логарифмическом вычете, принцип аргумента. Теорема Руше. Теорема Гурвица о пределе последовательностей аналитических функций. Определение вычета. Логарифмическая функция и логарифмический вычет. Кратность нуля и полюса для мероморфной функции
Предметная область: Математика и математический анализ
Описание: Ранее было рассмотрено определение последовательности непрерывных функций. Для данной последовательности имеет место следующая теорема: Теорема 2.1. Если функции непрерывны на множестве, то в случае равномерной сходимости их на к конечной функции, последняя также непрерывна на.
Дата добавления: 2015-06-12
Размер файла: 63.02 KB
Работу скачали: 8 чел.
Теорема о логарифмическом вычете, принцип аргумента. Теорема Руше. Теорема Гурвица о пределе последовательностей аналитических функций. Определение вычета. Логарифмическая функция и логарифмический вычет. Кратность нуля и полюса для мероморфной функции.
Сходимость аналитических функций
Ранее было рассмотрено определение последовательности непрерывных функций. Для данной последовательности имеет место следующая теорема:
В случае аналитических функций имеет место следующая фундаментальная теорема Вейерштрасса.
Имея это в виду, из (3) и (4) получаем при
Теорема о логарифмическом вычете
Доказательство. Используем теорему Коши о вычетах, согласно которой:
Отсюда следует, что:
При подсчете числа нулей регулярной функции в заданной области часто применяется теорема Руше.
Пусть, где полюс 1-го порядка. Значит, 1
C другой стороны, так как
Относительно равномерно сходящихся последовательностей регулярных функций докажем еще следующую теорему, имеющую многочисленные применения.
Если область содержит ∞, но отлична от полной плоскости, то, отобразив ее надлежащей дробно-линейной функцией на область, не содержащую ∞, можно применить к преобразованным функциям выше доказанное.
Логарифмический вычет
Вы́чет в компле́ксном анализе — объект (число, форма или когомологический класс формы), характеризующий локальные свойства заданной функции или формы.
Содержание
Одномерный комплексный анализ [ | ]
Вычет функции [ | ]
Вычет в «бесконечности» [ | ]
Цикл интегрирования в этом определении ориентирован положительно, то есть против часовой стрелки.
Аналогично предыдущему случаю вычет в бесконечности имеет представление и в виде коэффициента лорановского разложения в окрестности бесконечно удалённой точки:
Вычет дифференциальной формы [ | ]
Логарифмические вычеты [ | ]
Понятие логарифмического вычета используется для доказательства теоремы Руше и основной теоремы алгебры.
Способы вычисления вычетов [ | ]
Согласно определению вычет может быть вычислен как контурный интеграл, однако в общем случае это довольно трудоёмко. Поэтому на практике пользуются, в основном, следствиями из определения.
Приложения теории вычетов [ | ]
В большинстве случаев теория вычетов применяется для вычисления разного рода интегральных выражений с помощью основной теоремы о вычетах. Часто полезной в данных случаях бывает лемма Жордана.
Вычисления определённых интегралов от тригонометрических функций [ | ]
Вычисление несобственных интегралов [ | ]
Для вычисления несобственных интегралов с применением теории вычетов используют следующие две леммы:
∫ − ∞ + ∞ f ( x ) d x = 2 π i ∑ k = 1 n R e s z = z k f ( z ) <\displaystyle \int \limits _<-\infty >^<+\infty >\!f(x)\,dx=2\pi i\sum _
∫ − ∞ + ∞ f ( x ) e i α x d x = 2 π i ∑ k = 1 n R e s z = z k f ( z ) e i α z <\displaystyle \int \limits _<-\infty >^<+\infty >\!f(x)e^
При этом интегралы в левых частях равенств не обязаны существовать и поэтому понимаются только лишь в смысле главного значения (по Коши).
Электронная библиотека
Пусть функция w = f(z) – аналитическая в окрестности точки z0, за исключением самой точки (т.е. z0 – изолированная особая точка функции w = f(z)).
Вычет обозначается: или res f(z0) (происходит от слова resudi – остаток):
Теорема: Вычет относительно устранимой особой точки равен нулю.
Доказательство: Пусть z0 – устранимая точка, тогда функция
будет аналитическая в окрестности z0 и по теореме Коши что и требовалось доказать.
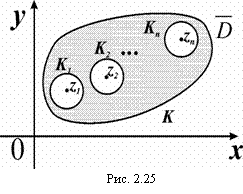
Доказательство: Опишем из каждой особой точки zК (k = 1, 2,…,n) как из центра, окружности Кк настолько малого радиуса, чтобы они целиком лежали в и не содержали других особых точек функции f(z) (рис. 2.25).
В многосвязной области f(z) будет аналитической. По теореме Коши:
Умножим и разделим правую часть последнего равенства на 2p I получим:
Что и требовалось доказать.
Найдем вычет относительно простого полюса. Пусть f(z) имеет в точке простой полюс, тогда
Как отмечено ранее она аналитическая в окрестности z0 и по формуле Коши
Вывод: вычет относительно простого полюса находят по формуле:
Найти вычет функции относительно точки z = 0.
Решение. Для функции точка z = 0 – простой полюс. Поэтому
Формула (2.88) получается сразу:
Решение. Согласно формуле (2.88)
так как z = 0 – простой полюс.
Решение. Функция имеет две особые точки z = 0 и z = 2; обе точки попадают в область, ограниченную окружностью |z| = 3.
Точка z = 0 – устранимая, так как
а вторая – простой полюс (сделайте рисунок).
Вычет относительно устраненной точки равен нулю. Вычет относительно точки z = 2 находим по формуле (2.88):
По основной теореме Коши о вычетах (2.85), получим:
Вывод формулы для нахождения вычета относительно кратного полюса аналогичен рассуждениям, проведенным для случая простого полюса, а именно: если f(z) имеет в точке z0 кратный полюс, то для функции (k – кратность полюса) точка z0 устранимая. Тогда функция
аналитическая в окрестностях z0. Значит,
Но на контуре поэтому
Вывод: получена формула для нахождения вычета функции относительно полюса порядка k:
Задачи для упражнений
Вычислить интегралы, используя основную теорему Коши о вычетах: