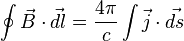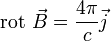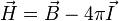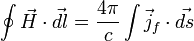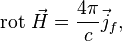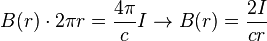теорема о циркуляции вектора магнитной индукции в дифференциальной форме

Закон Био-Савара. Теорема о циркуляции

Принцип суперпозиции: если магнитное поле работает за счет нескольких проводников с током, тогда индукция результативного поля – это совокупность индукций полей, которые создаются каждым проводником по отдельности.

Индукция B → проводника с током представлена, как векторная сумма элементарных индукций ∆ B → вырабатываемых отдельными участками проводника. На практике нельзя отделить один участок проводника с током, поскольку постоянные токи всегда замкнутые. Возможно лишь измерить совокупную индукцию магнитного поля, которое создают все элементы тока. Как найти индукцию магнитного поля?

Закон Био–Савара

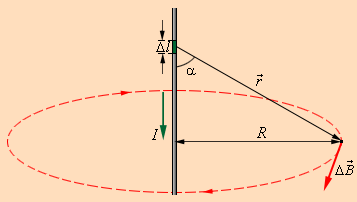
В формуле r – это расстояние от заданного участка Δ l до точки наблюдения, α – это угол между направлением на точку наблюдения и направлением тока на заданном участке, μ 0 – это магнитная постоянная.

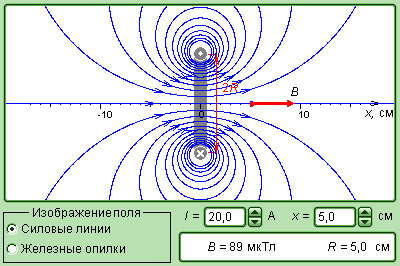
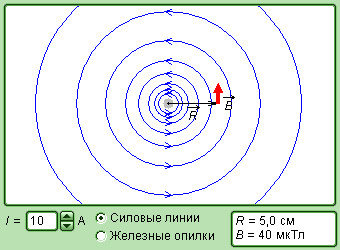
С помощью этого закона можно определять магнитные поля токов с различными конфигурациями. Запросто рассчитать магнитное поле в центре кругового витка с током. Вычисления приводят к соотношению:

где R – это радиус кругового проводника.

Чтобы определить направление вектора B → тоже используется правило буравчика, только в этом случае рукоятка вращается по направлению кругового тока, а поступательное движение буравчика указывает, куда направлен вектор магнитной индукции.

Теорема о циркуляции вектора магнитной индукции

Вычисления магнитного поля зачастую упрощаются с учетом симметрии в конфигурации токов. В этом помогает теорема о циркуляции вектора магнитной индукции.

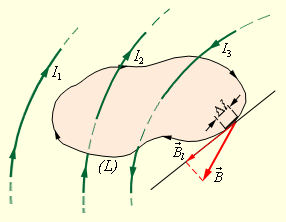
Некоторые токи, при которых магнитное поле создается, пропускают выбранный контур L тем временем, как остальные токи находятся в стороне от контура.

Согласно теореме о циркуляции, циркуляция вектора B → магнитного поля постоянных токов по любому из контуров L все время определяется, как произведение магнитной постоянной μ 0 на сумму всех токов:

∑ ( L ) B l ∆ l = μ 0 ∑ l i.

Теорема о циркуляции в этом примере математически выражается следующей формулой:

Общий вид теоремы о циркуляции можно вывести из принципа суперпозиции и закона Био-Савара.

отсюда можно вывести формулу для модуля магнитной индукции поля прямолинейного проводника с током, приведенную раньше.

Из данного примера видно, что теорема о циркуляции вектора магнитной индукции B → можно использовать для вычисления магнитных полей, которые создаются симметричным распределением токов, когда можно наугад определить общую структуру поля.

Существует много примеров определения магнитных полей при помощи теоремы о циркуляции.

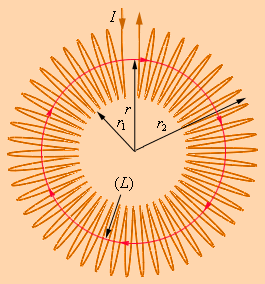
Предположим, что катушка намотана виток к витку на ненамагниченный тороидальный сердечник. В ней линии магнитной индукции сходятся внутри катушки и выступают концентрическими окружностями. Они имеет такое направление, что, смотря вдоль них, наблюдатель увидел бы ток в витках, циркулирующих по часовой стрелке.

Однако в пределе каждая часть тороидальной катушки при необходимости рассматривается в качестве длинной прямолинейной катушки, которая называется соленоид. Вдали торцов такой катушки модуль магнитной индукции определяется, как соотношение в случае с тороидальной катушкой.

Данное вычисление совпадает с формулой для магнитного поля тонкой тороидальной катушки.

Источник

§ 37. ТЕОРЕМА О ЦИРКУЛЯЦИИ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ

ВИХРЕВОЙ ХАРАКТЕР МАГНИТНОГО ПОЛЯ.

Теорема о циркуляции вектора магнитной индукции поля постоянных токов в вакууме может быть доказана на основе закона Био-Савара, что, в общем случае, достаточно сложно.

— циркуляция вектора магнитной индукции по любому замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов охватываемых этим контуром.

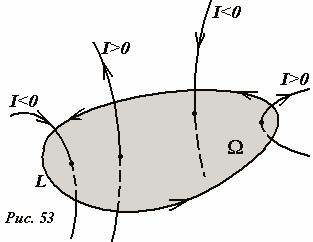
Ток считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта (рис.75).

Если ток распределен по объему, в котором расположен контур, то полный ток охваченный контуром , где интеграл берется по произвольной поверхности натянутой на контур, плотность тока соответствует токе расположения площадки . В этом случае теорема о циркуляции:

Покажем справедливость теоремы на примерах.

ПРИМЕР 1. Контур охватывает прямолинейный бесконечно длинный провод с током, причем контур расположен в плоскости перпендикулярной проводу (рис.76). Найдем циркуляцию вектора магнитного поля, используя формулу для расчета индукции поля, полученную методом суперпозиции . Скалярное произведение под интегралом можно представить (рис.77):

Если замкнутый контур L` не охватывает ток (рис.78),

То и циркуляция также равна нулю.

ПРИМЕР 2. Контур лежит не в плоскости перпендикулярной проводу (рис.79). Разложим вектор на составляющие вектора, один из которых лежит в плоскости перпендикулярной проводу, а второй перпендикулярен этой плоскости:

Циркуляция вектора магнитной индукции определяется только «проекцией» контура на плоскость перпендикулярную проводу.

ПРИМЕР 3. Если контур охватывает несколько токов, то вектор индукции результирующего поля:

ПРИМЕР 4. Если ток непрерывно распределен в объеме, в котором расположен контур, то полный ток, охватываемый контуром , где интеграл берется по произвольной поверхности натянутой на контур.

Тогда :

РИС.80 РИС.81 РИС.82 РИС.83

Теорема о циркуляции позволяет достаточно просто рассчитать индукцию магнитного по известному распределению токов, если можно выбрать контур, вдоль которого модуль вектора магнитной индукции и направление постоянно.

В простейшем варианте можно выбрать контур полностью совпадающий с линией магнитной индукции как в поле прямого тока (рис.80), тороида (рис.81).

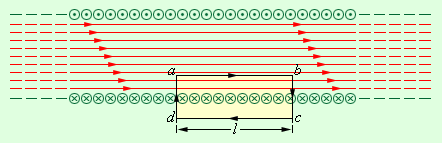
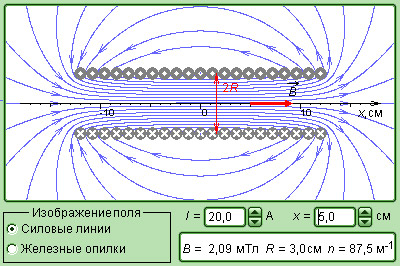
Поле внутри соленоида (рис.82) тем более однородно, чем больше длина соленоида по сравнению с его диаметром. Для «бесконечного» соленоида снаружи вблизи его поверхности магнитного поля нет и можно выбрать контур, лишь часть которого совпадает с линией магнитной индукции (рис.83).

Ток охватываемый контуром , где N – число витков с током, охваченных контуром. Тогда:

Следовательно, индукцию магнитного поля внутри «бесконечного» соленоида можно рассчитать по формуле

, где n – число витков соленоида на единицу длины.

Факт, что циркуляция вектора магнитной индукции по замкнутому контуру не равна нулю, означает, что, в отличие от электростатического, магнитное поле – не потенциально.

Используем теорему Стокса и сравним это выражение с записью теоремы о циркуляции вектора магнитной индукции в случае непрерывного распределения тока в некотором объеме.

— дифференциальная (локальная) форма теоремы о циркуляции. Математическая констатация того факта, что линии вектора магнитной индукции замкнуты вокруг вектора плотности тока по правилу правого буравчика и поэтому магнитное поле называют вихревым или соленоидальным.

Используем, что или с помощью определителя:

, .

Источник

Теорема о циркуляции магнитного поля

Теорема о циркуляции магнитного поля — одна из фундаментальных теорем классической электродинамики, сформулированная Андре Мари Ампером в 1826 году.

Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.

В математической формулировке для магнитостатики теорема имеет следующий вид

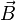
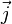
Здесь — вектор магнитной индукции, — плотность тока; интегрирование слева производится по произвольному замкнутому контуру, справа — по произвольной поверхности, натянутой на этот контур. Данная форма носит название интегральной, поскольку в явном виде содержит интегрирование. Теорема может быть также представлена в дифференциальной форме

Эквивалентность интегральной и дифференциальной форм следует из теоремы Стокса.

Приведённая выше форма справедлива для вакуума. В случае применения её в среде (веществе), она будет корректна только в случае, если под j понимать вообще все токи, то есть учитывать и «микроскопические» токи, текущие в веществе, включая «микроскопические» токи, текущие в областях размерами порядка размера молекулы и магнитные моменты микрочастиц.

Поэтому в веществе, если не пренебрегать его магнитными свойствами, часто удобно из полного тока выделить ток намагничения, выразив его через величину намагниченности 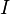и введя вектор напряжённости магнитного поля

Тогда теорема о циркуляции запишется в форме

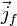
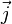
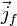
где под (в отличие от в формуле выше) имеются в виду т. н. свободные токи, в которых ток намагничения исключен (что бывает удобно практически, поскольку — это обычно уже в сущности макроскопические токи, которые не связаны с намагничением вещества и которые в принципе нетрудно непосредственно измерить).

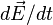
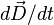
В динамическом случае — то есть в общем случае классической электродинамики — когда поля меняются во времени (а в средах при этом меняется и их поляризация) — и речь тогда идет об обобщенной теореме, включающей , — всё сказанное выше относится и к микроскопическим токам, связанным с изменениями поляризации диэлектрика. Эта часть токов тогда учитывается в члене .

Теорема о циркуляции играет в магнитостатике приблизительно ту же роль, что и теорема Гаусса в электростатике. В частности, при наличии определённой симметрии задачи, она позволяет просто находить величину магнитного поля во всём пространстве по заданным токам. Например, для вычисления магнитного поля от бесконечного прямолинейного проводника с током по закону Био — Савара — Лапласа потребуется вычислить неочевидный интеграл, в то время как теорема о циркуляции (с учётом осевой симметрии задачи) позволяет дать мгновенный ответ:

вопрос 47. Квантовая статистика электронов в металлах. Функция Ферми. Уровни Ферми. Выроденное состояние электронного газа в металлах.

Квантовая статистика базируется на принципе Паули, согласно которому в каждом энергетическом состоянии может находиться только один электрон. Отсюда сразу вытекает различие классического и квантового распределений электронов по энергиям. С классической точки зрения энергия всех электронов при температуре абсолютного нуля должна равняться нулю. А по принципу Паули даже при абсолютном нуле число электронов на каждом уровне не может превышать двух. И если общее число свободных электронов в кристалле равно n, то при 0 К они займут n 2 наиболее низких энергетических уровней.

В квантовой теории вероятность заполнения энергетических состояний электронами определяется функцией Ферми:

-1 (8.7)

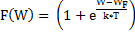
где W — энергия уровня, вероятность заполнения которого определяется, W_F — энергия характеристического уровня, относительно которого кривая вероятности симметрична.

Таким образом, величина W_F определяет максимальное значение энергии, которую может иметь электрон в металле при температуре абсолютного нуля. Эту характеристическую энергию называют энергией Ферми или уровнем Ферми. Соответствующий ей потенциал j = W_F/e называют электрохимическим потенциалом. Следует отметить, что энергия W_F не зависит от объема кристалла, а определяется только концентрацией свободных электронов, что непосредственно вытекает из принципа Паули.

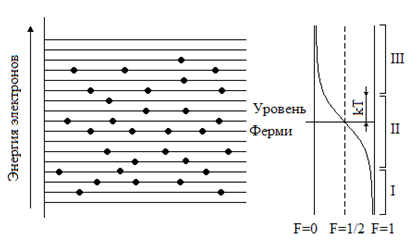
При нагревании кристалла ему сообщается тепловая энергия порядка kT. За счет этого возбуждения некоторые электроны, находящиеся вблизи уровня Ферми, начинают заполнять состояния с более высокой энергией: график функции распределения становится несколько пологим.

Распределение электронов в частично заполненной зоне (а) и функция вероятности заполнения электронами уровней (б): I – уровни, заполненные; II – интервал размывания; III – уровни, полностью свободные

Из формулы (8.7) легко видеть, что при любой температуре для уровня с энергией W =W_F вероятность заполнения электронами равна 0,5. Все уровни, расположенные ниже уровня Ферми, с вероятностью больше 0,5 заполнены электронами. Наоборот, все уровни, лежащие выше уровня Ферми, с вероятностью более 0,5 свободны от электронов.

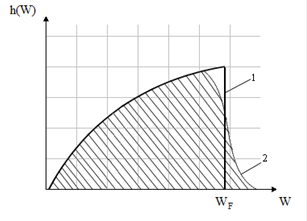
Распределение электронов по энергиям в металле можно представить параболической зависимостью, изображенной на рисунке 8.3. Электроны, расположенные в глубине от уровня Ферми, не могут обмениваться энергией с кристаллической решеткой, ибо для них все ближайшие энергетические состояния заняты.

Системы микрочастиц, поведение которых описывается статистикой Ферми–Дирака, называют вырожденными. В состоянии вырождения средняя энергия электронного газа практически не зависит от температуры. Электронный газ в металле остается вырожденным до тех пор, пока любой из электронов не сможет обмениваться энергией с кристаллической решеткой, а это, в свою очередь, возможно лишь тогда, когда средняя энергия тепловых колебаний станет близкой к энергии Ферми. Для металлов температура снятия вырождения T_F по порядку величины составляет 10 4 К, т.е. превышает не только температуру плавления, но и температуру испарения металлов.

Вследствие вырождения в процессе электропроводности могут принимать участие не все свободные электроны, а только небольшая часть их, имеющая энергию, близкую к энергии Ферми. Только эти электроны способны изменять свои состояния под действием поля. Электрический ток, возникающий в металле под влиянием разности потенциалов, отражает изменения в распределении электронов по скоростям. В соответствии с квантовой статистикой это распределение является производным от распределения по энергиям и симметрично в отсутствие внешнего поля. Под действием электрического поля происходит рассеяние электронов под большими углами в процессе их упругих столкновений с узлами решетки. В результате этого возникает избыток быстрых электронов, движущихся против поля, и дефицит быстрых электронов с противоположным направлением скорости.

При изменении температуры энергия Ферми W_F изменяется незначительно, что является спецификой вырожденного состояния электронного газа. Столь малые изменения в таком широком температурном диапазоне можно не учитывать. Концентрации свободных электронов в чистых металлах различаются незначительно. Температурное изменение n также очень мало. Поэтому проводимость определяется в основном средней длиной свободного пробега электронов, которая, в свою очередь, зависит от строения проводника, т.е. химической природы атомов и типа кристаллической решетки.

вопрос 48. Теплообмен при ламинарном обтекании плоской изотермической пластины.

Ламинарное течение — течение, при котором жидкость или газ перемещается слоями без перемешивания и пульсаций (то есть беспорядочных быстрых изменений скорости и давления).

Источник

Учебники

Журнал «Квант»

Общие

§12. Постоянное магнитное поле

12.12 Циркуляция вектора индукции. Теорема о циркуляции магнитного поля.

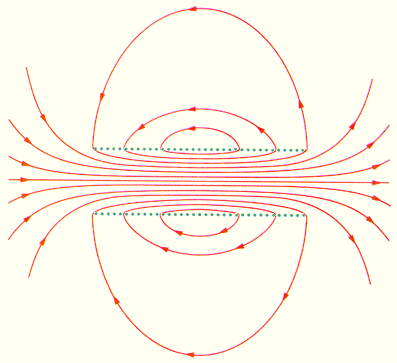
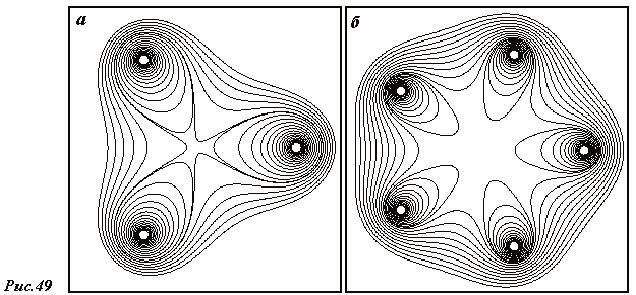
Силовые линии магнитного поля являются замкнутыми кривыми, поэтому картины силовых линий магнитного поля напоминают линии тока жидкости, движущейся с завихрениями. Посмотрите еще раз на приведенные ранее картины силовых линий магнитного поля – сплошные вихри. На рис. 49 показаны еще два примера силовых линий магнитного поля, созданного длинными параллельными проводниками (на рис. 49.а – их три, а на рис. 49.б – пять), по которым протекают равные токи.

Для математического описания таких полей удобно использовать понятие циркуляции вектора.

Точнее следует сказать, что знание циркуляции необходимо для описания любого векторного поля: напомним, любое векторное поле определяется однозначно, если известны теоремы о потоке и циркуляции векторов этого поля. Другое дело, что в электростатическом поле циркуляция вектора по любому контуру равна нулю, поэтому электростатическое поле является потенциальным и для него оказывается возможным ввести такую важную физическую характеристику как потенциал поля. Для магнитного поля циркуляция не имеет явного физического смысла, а является весьма полезной вспомогательной математической величиной.

Определение циркуляции вектора магнитной индукции, аналогично определению циркуляции любого векторного поля.

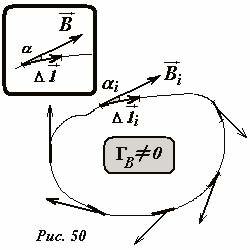
Рассмотрим произвольную замкнутую линию (не обязательно, чтобы это была силовая линия). Выделим на этой линии малый участок, определяемый вектором \(

\Delta \vec l\) (рис. 50). Пусть вектор индукции магнитного поля на этом участке равен \(

\Delta \vec l\)). Далее разобьем всю замкнутую линию (Рис. 50) на малые участки \(

Построенная таким образом, математическая конструкция называется циркуляцией вектора магнитной индукции по заданному контуру L. Ее величина может быть как положительной, так и отрицательной, ее знак определяется произвольным выбором направления обхода контура, но, как обычно, положительным принимается направление обхода против часовой стрелки.

Понятно, что циркуляция магнитного поля может отличаться от нуля. Например, если в качестве произвольного контура выбрать замкнутую силовую линию, то при ее обходе на всех участках вектор индукции будет совпадать по направлению с направлением касательной, как было сказано ранее, «все время будем плыть по течению».

Теперь нам необходимо установить теорему, позволяющую установить циркуляцию вектора индукции. Отметим, что эта теорема является прямым следствием закона Био-Саварра-Лапласа, можно сказать, иной математической формулировкой этого физического закона. Не будем заниматься строгим доказательством теоремы, а проиллюстрируем ее простым примером.

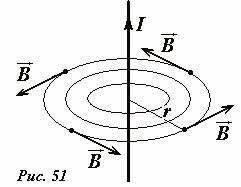
Пусть магнитное поле создается длинным прямым проводником, по которому протекает электрический ток силой I. Индукцию такого поля мы рассчитали: силовые линии являются концентрическим окружностями с центрами на проводнике (Рис. 51). Легко подсчитать циркуляцию вектора индукции (1) по контуру, совпадающему с одной из силовых линий (например, радиуса r). Действительно, на любом участке этого контура вектор индукции направлен по касательной (поэтому все α_i = 0), а модуль вектора индукции постоянен и равен \(

Так как для вектора магнитной индукции справедлив принцип суперпозиции, а циркуляция линейно выражается линейно через индукцию поля, по принцип суперпозиции также справедлив и для циркуляции магнитного поля.

Обобщая все эти положения, дадим окончательную формулировку теоремы о циркуляции: циркуляция вектора магнитной индукции по любому контуру равна сумме токов, пересекающих контур, умноженной на магнитную постоянную

Сумма токов, пересекающих контур \(

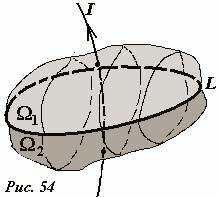
Наконец, уточним, что значит «ток пересекает контур», особенно, если контур не является плоским. Контур это замкнутая линия, поэтому приведенное выражение следует понимать, как ток пересекает любую поверхность (Рис. 54), опирающуюся на контур (или еще говорят «поверхность, натянутую на контур»). Легко доказать, что эта сумма токов, не зависит от выбора поверхности, натянутой на данный контур: из закона сохранения электрического заряда следует, что в статическом случае (когда все токи и все заряды не изменяются с течением времени) сумма токов, пересекающих любую замкнутую поверхность, равна нулю («сколько втекает, столько же вытекает»).

Источник