Тренажер устного счета
Данный тренажер является одним из тренажеров по математике для развития навыков устного счета с удобным, интуитивно-понятным интерфейсом.
Онлайн тренажер устного счета
Принцип работы основан на генерации примеров по математике подходящего вам уровня сложности для всех классов, решение которых способствует развитию навыков устного счёта.
Приложение благоприятно влияет на умственную деятельность как детей, так и взрослых.
Разнообразие режимов
На странице настроек режима можно задавать необходимые параметры генерации примеров по математике для любого класса.
Тренажер устного счета позволяет отрабатывать 4 небезызвестных арифмитических действия на шести уровнях сложности.
Далее корректируете вид математического примера выбирая тип, устанавливая количество слагаемых, манипулируя числовыми множествами.
На данном этапе разработки были продуманы и реализованы режимы, позволяющие работать с двумя множествами чисел: Положительными и Отрицательными. В каждом из ним можно попрактиковаться в различных типах заданий: «Пример», «Уравнение», «Сравнение».



Все изменения настроек сразу применяются и Вы тут же можете увидеть как будет выглядеть новый пример в графе «Например». А когда подбор нужных характеристик окончен, нажмите на кнопку ПОЕХАЛИ.
Бонусом является возможность загрузить и в дальнейшем распечатать «самостоятельную работу» в формате PDF, состоящую из 26 примеров соответствующего режима, кликнум по значку Принтер.
Процесс счёта
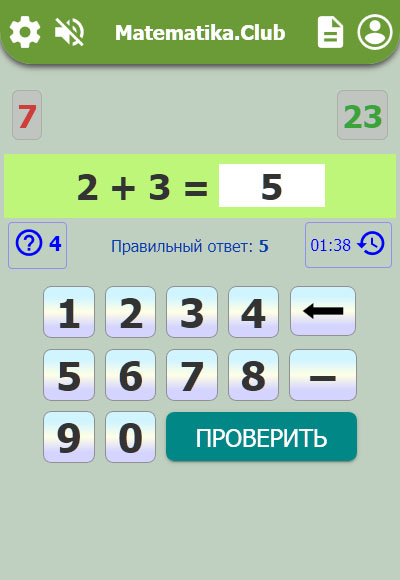
Вверху представлены 4 кнопки быстрого доступа: к главной странице сайта, профилю пользователя. Также есть возможность включить/отключить звковые уведомления или перейти к Протоколу ошибок и подсказок.
Вы решаете заданый пример, вводите ответ с помощью экранной клавиатуры, нажимаете на кнопку ПРОВЕРИТЬ. Если затрудняетесь дать ответ, воспользуйтесь подсказкой. После проверки результат Вы увидите сообщение либо о правильно введенном ответе, либо об ошибке.
Если по какой-либо причине вы хотите обнулить свои результаты, нажмите на иконку «Сбросить результат» спарва.
Игровая форма
Приложение также предусматривает игровую анимацию «Сражение фехтовальщиков».
Такой интерфейс делает процесс решения математических примеров более интересным, являясь также простой мотивацией для детей.
Если режим с анимацией вам мешает, его можно отключить на странице установок с помощью иконки
Протокол ошибок
В любой момент работы с тренажером вы можете перейти к разделу приложения «Протокол ошибок», кликнув на соответствующую иконку сверху, либо перелестнув страницу вниз.
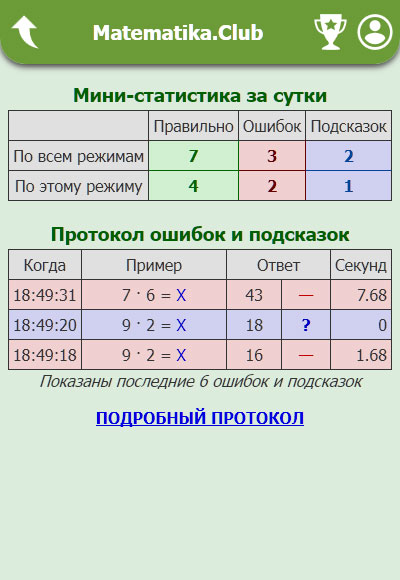
Здесь вы сможете посмотреть свою статистику (количество примеров по категориям) за последние сутки и по последнему режиму.
А также увидеть список ошибок и подсказок (максимум 6 штук), либо перейти к подробной статистике.
Дополнительная информация
Хотим также обратить внимание, что ссылка на какой-либо режим имеет довольно простой вид:
домен сайта + раздел приложения + кодировка данного режима
например: matematika.club/app/#12301
Таким образом Вы легко можете пригласить любого человека посоревноваться в решении арифметических примеров по математике, просто передав ему ссылку на текущий режим.
Тренажёр устного счёта
Онлайн-тест для проверки знания таблицы умножения и навыков устного счёта. Выберите арифметическое действие, кол-во вопросов в тесте и приступайте к проверке навыков сложения, вычитания, деления или умножения.
Кол-во вопросов в тесте
Тренируйте устный счёт эффективно
Тренажёр устного счёта предназначен для проверки знания таблицы умножения и тренировки вычислительных навыков: умения складывать и вычитать, делить и умножать. Тренажёр развивает память, концентрацию и скорость реакции, помогает ученикам начальной школы довести навыки устного счёта до автоматизма, а старшеклассникам — быстро освежить в памяти таблицу умножения перед школьной контрольной или экзаменом.
Учитесь всерьёз и надолго
Для облегчения запоминания вопросов в тренажёре на Блицтесте реализована система умного повторения — эффективный способ запоминания информации. Система включается автоматически для авторизованных пользователей. Просто выбирайте цель и приступайте к учёбе.
Таблица умножения
Сложение в пределах от 10 до 20
Сложение в пределах 10
Сложение в пределах 20 с переходом через десяток
Повышайте успеваемость в школе
Регулярные тренировки в тренажёре развивают навыки устного счёта и гарантируют рост успеваемости по математике в школе.
Задача математики в начальной школе — научить детей решать примеры на четыре арифметических действия: сложение, вычитание, умножение и деление. Школа учит детей считать письменно, но не менее важно развивать навыки устного счёта. В тренажёре удобно учить умножение и деление в пределах 100 и практиковаться в устном счёте в рамках программы математики начальной школы. Режимы повышенной трудности помогут старшеклассникам закрепить вычислительные навыки, необходимые при решении задач по геометрии и тригонометрии.
Базовый курс математики
Тренажёр устного счёта развивает математические навыки, а курс «Математика начальной школы» даёт конкретные математические знания. В курсе сформулированы основополагающие термины и правила, без которых немыслимо изучение математики старших классов:
Развивайте память и концентрацию
В жизни мы ежедневно сталкиваемся с задачами, требующими быстрого решения. Продавец взвесил яблоки и назвал стоимость. Если он ошибся, у нас есть несколько секунд, чтобы его поправить, прежде чем оплатить покупку. Онлайн-тренажёр устного счёта развивает скорость реакции, тренирует память и концентрацию, позволяет довести навыки устного счёта до автоматизма.
Тренируйте только нужное
Выбирайте в Тренажёре устного счёта нужные арифметические действия и один или несколько множителей, делителей, слагаемых или вычитаемых. Используйте настройки тренажёра для тренировки устного счёта с заданным числом, прохождения полного теста по таблице умножения, решения примеров повышенной сложности с отрицательными числами или устного счёта с большими числами.
Опирайтесь на подсказки
Тренажёр устного счёта не только удобный инструмент контроля знаний, но и надёжный помощник в освоении и развитии математических навыков. По ходу онлайн-теста тренажёр выводит для каждого примера подсказки: состав числа или конкретные математические выражения, дополняющие пример.
Регулируйте сложность примеров
Тренируйте сложение и вычитание в пределах двадцати или включите режим «Большие числа» и считайте в пределах ста с переходом через десятки. Регулируйте трудность примеров на умножение и деление: оставайтесь в рамках таблицы умножения или умножайте и делите в т.ч. и на двузначные числа. Используйте переключатель «Отрицательные числа» для добавления в примеры чисел меньше нуля.
Учитесь играючи!
Развивающие и образовательные игры — сила. Фокусировка внимания и позитивная мотивация в игре гарантируют крепкое усвоение материала.
Мы позаботились о простоте и удобстве тренажёра для детей и постарались оптимизировать его для мобильных устройств и планшетов. Для самых маленьких пользователей, которым сложно сохранять концентрацию, мы сделали возможность ограничить тест пятью вопросами и добавили в тренажёр космонавта, звёздочки, звуки, анимацию и конфетти.
Тренажёр устного счёта — бесплатный сервис, но в него вложено огромное количество усилий и средств. Поддержите нас — станьте частью Блицтеста!
Александр Мартынов
Руководитель Блицтеста
Устный счет
Устный счет существует столько же, сколько существует человечество. В разные времена навыки быстрого счета играли большую роль в развитии не только людей, но и всего человечества. Сейчас наука продвинулась так далеко, что для вычислений используются мощные компьютеры, и человек просто не в силах сделать столько вычислений, сколько необходимо для одного только запуска большого адронного коллайдера или обычного смартфона.
Но даже сейчас, когда компьютерные системы ведут бухгалтерию миллионов компаний, автоматизируют все сложные и рутинные операции на предприятиях, заводах, аэропортах и даже в магазинах – быстрый счет не потерял и не потеряет своей актуальности.
Примеры упражнений для устного счета
Фруктовая математика
Игра «Фруктовая математика» поможет вам усовершенствовать свое мышление. Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.
Числовой охват
Надо запомнить цифры и воспроизвести их в правильном порядке. Можно пользоваться клавиатурой.
Навыки устного счета
Навыки устного счета бывают разными и перед тем как идти дальше ответьте, пожалуйста, на несколько вопросов:
Это были вопросы для размышления. Они помогают не только вовлечь Вас в процесс, показать альтернативные варианты, когда навыки быстрого счета бывают очень нужны. Подумайте, возможно Вы найдете еще плюсы, того какую пользу еще может принести этот математический навык.
Если Вы ответили «Да» хотя бы на один из вопросов, то надеюсь, что Вы научитесь лучше считать в уме.
Уроки устного счета
Чтобы научиться быстро считать в уме, Вам понадобится каждый день тренировать свой мозг. Выполняйте упражнения устного счета по 15-30 минут в день. Уже в первые дни заметите результат, большинство добиваются успехов уже на первом занятии.
Помню, у меня было так же, когда я уже давно ничего не считал и решил посмотреть, что осталось от моих былых способностей. Поначалу считал очень медленно, но потом получалось все быстрее и быстрее.. На первом занятии я стал быстро складывать почти все трехзначные числа. В процессе счета очень важную роль играет развитие памяти. Чем лучше развита память, тем быстрее запоминаются наиболее частые комбинации.
В результате мозг запоминает разные варианты и быстрее выдает результат. Поэтому счет потом идет больше по памяти, чем по вычислениям. Для вычисления сложных действий могут браться результаты более простых из памяти.
Уроки устного счета онлайн
Игры для развития устного счета
Вы когда-нибудь задумывались: «Как можно тренировать счет легко и интересно?«. Скорее всего да, потому что тренировать устный счет традиционным способом, как это принято в школе очень тяжело.
Наш мозг любит играть, он любит интересные задания, где виден прогресс в графиках или очках. Именно поэтому многие ученые в последнее столетие изучают работу мозга. Они обнаружили, что навыки развиваются лучше всего именно в игровой форме. Играйте по 3-5 игр в день, по 2 минуты и Вы увидите результат. Скорость Ваших ответов и набираемые очки будут постепенно увеличиваться.
Игра «Угадай операцию»
Это одно из лучших упражнений для тренировки счета, потому что вам потребуется вставить правильно математические знаки, чтобы получить верный результат. Это упражнение поможет вам развить устный счет, логику и скорость мысли. С каждым верным ответом сложность увеличивается.
Игра «Математические матрицы»
«Математические матрицы» великолепное упражнение для развития устного счета, которое поможет развить мыслительную работу мозга, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке показано число «29», а искомая пара «5» и «24».
Игра «Копилка»
Не могу удержаться, чтобы не посоветовать вам игру «Копилка» с того же самого сайта, на котором вам нужно зарегистрироваться, указать только E-mail и пароль. Эта игра сможет устроить вам фитнес для мозга и отдых для тела. Суть игры в том, чтобы указать 1 из 4 окошечек, в котором сумма монет наибольшая. Сумеете ли вы показать прекрасный результат? Мы ждем вас.
Игра «Математические сравнения»
Представляю прекрасную игру «Математические сравнения», с которой вы сможете расслабиться телом, а напрячься мозгом. На скриншоте показан пример данной игры, в которой будет вопрос, связанный с картинкой, а вам надо будет ответить. Время ограниченно. Как много вы успеете ответить?
Игра «2 назад»
Для развития устного счета советуем упражнение «2 назад». Эта игра помогает в развитии устного счета, памяти и внимания. На экран будет показана последовательность цифр, которые нужно запомнить, а затем сравнить цифру последней карты с предыдущей. Это упражнение тренирует не только устный счет, но и мозг в целом. Упражнение доступно после регистрации, вы готовы? Развивайтесь с нами.
Игра «Визуальная геометрия»
Помимо этих упражнений есть еще более 30 бесплатных развивающих игровых-тренажеров, которые доступны сразу после регистрации.
Для получения доступа к бесплатным играм нужно зарегистрироваться указать только Ваш Email и пароль (или авторизоваться с помощью соц. сетей).
Устный счёт на ЕГЭ и ГИА
Устный счёт так же может пригодиться на экзаменах по математике, в том числе и на едином государственном экзамене, который пишут все школьники одиннадцатых классов. Этот навык поможет меньше мучиться со сложными вычислениями. Разбейте их на более мелкие математические операции, которые легче посчитать в уме.
Устный счёт улучшает не только ваши вычислительные способности, но и другие мыслительные стратегические операции, такие как память, что позволит ещё быстрее и качественнее запоминать любую информацию и применять свои новые способности не только на экзаменах, но и в своей повседневной жизни.
Чтобы научиться быстрее считать и лучше подготовиться к ЕГЭ или ГИА, запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика». Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Устный счет по математике
Взрослым и детям школьного возраста отлично подойдут тренинги и уроки устного счета. Особенно они нужны детям, потому что они только учатся считать, но школьникам 1,2 и 3 классов нужны более простые уроки устного счета по математике.
Для школьников начальных классов вполне хватит простых арифметических упражнений. Но зато как их можно натренировать, особенно если сделать это в игровой форме.
Игра «Числовой охват: Революция»
Интересная и полезная игра «Числовой охват: Революция», которая поможет Вам улучшить память. Суть игры в том, что на мониторе будут выводиться цифры по порядку, по одной, которые Вам следует запомнить, а затем воспроизвести. Такие цепочки будут состоять из 4, 5 и даже 6 цифр. Время ограниченно. Побейте дневной рекорд среди всех игроков.
Курсы для развития устного счета и мозга
Ускоряем устный счет, НЕ ментальная арифметика
Секретные и популярные приемы и лайфхаки, подойдет даже ребенку. Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого вычитания, сложения, умножения, деления, расчета процентов, но и отработаете их в специальных заданиях и развивающих играх. Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Развитие памяти и внимания у ребенка 5-10 лет
Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.
После прохождения курса ребенок сможет:
Супер-память за 30 дней
В течение 30 дней после подписки Вы будете получать интересные упражнения и развивающие игры на свою почту, которые сможете применять в своей жизни.
Мы будем учиться запоминать все, что может потребоваться в работе или личной жизни: учиться запоминать тексты, последовательность слов, цифры, изображения, события, которые произошли в течение дня, недели, месяца и даже карты дорог.
Как улучшить память и развить внимание
Бесплатное практическое занятие от advance.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Если вы хотите разогнать свой мозг, улучшить его работу, подкачать память, внимание, концентрацию, развить больше креативности, выполнять увлекательные упражнения, тренироваться в игровой форме и решать интересные задачки, тогда записывайтесь! 30 дней мощного фитнеса мозга Вам гарантированы:)
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, копить деньги и в дальнейшем инвестировать их.
Скорочтение за 30 дней
Запишитесь на курс Скорочтение за 30 дней, чтобы научиться читать в 3-4 раза быстрее. С 2015 года по нашей программе обучилось 1507 человек из Москвы, Санкт-Петербурга, Екатеринбурга, Новосибирска, Казани, Челябинска, Уфы, Оренбурга, Нижнего Новгорода, Киева, Минска и других городов.
В этой статье я дал общее представление об устном счете, способах развития устного счета, тренажерах, рассказал про курс «Ускоряем устный счет, НЕ ментальная арифметика», который поможет научиться считать на сверхзвуковой скорости.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Список уроков
Нажми «Продолжить» для возвращения к примерам или «Главная» для перехода на главную страницу к списку уроков (результат урока при этом сохранится)
примеров решено, пора отдохнуть.
Нажми «Продолжить» для возвращения к примерам или «Главная» для перехода на главную страницу к списку уроков (результат урока при этом сохранится)
Урок пройден!
Отлично! Урок успешно завершен, теперь можно переходить к следующему. Ты просто умница! Результаты по этому уроку можно посмотреть, нажав на кнопку «Статистика» в верхнем меню
Статистика по урокам
*Для расчета среднего времени используются лучшие 95% из всех результатов
Описание тренажера. Немного теории
Родителям / Наставникам
Тренажер устного счета для сложения и вычитания
Программа сложения и вычитания от 0 до 100 предназначена для развития у детей навыков уверенного счета и выбора эффективного метода вычисления результата в уме.
Программа состоит из 6 основных этапов, разделенных на 25 уроков. Каждый урок развивает определенный вычислительный навык, либо открывая новый этап вычислений, либо повторяя предыдущие для закрепления достигнутого результата. Важно, чтобы ребенок изучал уроки последовательно и переходил к следующему только после того, как завершен предыдущий (степень готовности 100%), что означает полное усвоение текущего материала. Это позволит надежно закрепить навыки счета и быстрее освоить следующие уроки без необходимости возвращаться к предыдущим урокам и пояснениям.
Программа сложения и вычитания двузначных чисел предполагает, что в процессе курса ученик тренирует сложение чисел меньше 10, овладевает понятием десятка, начальными навыками сложения и вычитания двузначных чисел и чисел меньше 10, в том числе с переходом через десяток.
Вторая часть курса предназначена для обучения и закрепления навыков более комплексного сложения и вычитания двузначных чисел с результатом, находящимся в пределах 100.
Основные этапы и их особенности
Этап 1 — счет в пределах 10
Это простейший этап, переходный от присчитывания (N+1, N-1) к настоящему сложению и вычитанию. На этом этапе для ребенка важно усвоить несколько базовых принципов. Первое — понять, что сложение или вычитание любых двух чисел можно представить, как присчитывание, то есть сложение или вычитание числа и нескольких единиц (5+3=5+1+1+1=6+1+1=7+1=8, 8-2=8-1-1=7-1=6). Таким образом, ребенок легко сможет складывать и вычитать числа больше единицы. Важно следить, чтобы к концу этого этапа ребенок от присчитывания перешел к сложению и вычитанию чисел целиком, без раскладывания второго аргумента на несколько единиц (5+3=8, 8-2=6). Второе — ребенок должен усвоить, что при сложении можно свободно переставлять слагаемые, а также понять, что к большему числу удобнее прибавлять меньшее, чем наоборот (2+6=6+2, при этом удобнее и быстрее к шести прибавить два, чем к двум шесть).
Вариантом этого этапа является сложение и вычитание чисел внутри десятка, но без перехода через десяток (19-5=14, 12+4=16). Важным принципом здесь для ребенка является то, что операции внутри десятка не зависят от того, с каким десятком мы работаем. Следует убедиться, что ребенок усвоил независимость операций с единицами от десятков, прежде чем переходить к следующему этапу. Сперва этот тип вычислений встречается в виде операций с числами от 10 до 20, позднее для закрепления навыков в последующих уроках будут встречаться такие же операции в любых десятках вплоть до 100.
Этап 2 — понятие десятка
Ключевым этапом для перехода к операциям над двузначными числами является введение понятия десятка. Ребенок должен научиться разделять десятки и единицы и проводить операции над десятками независимо от единиц. Для этого сначала используются примеры, позволяющие переходить от полного десятка к неполному и наоборот (10+5=15, 19-9=10), а также примеры, отнимающие от неполного десятка его полную часть (19-10=9). В результате ребенок должен научиться отделять десятки от единиц и оперировать отдельно тем и другим. Вначале используются операции в пределах 10-20, впоследствии добавляются операции в более старших десятках.
Для закрепления понятия десятка, как самостоятельного элемента, используются примеры со сложением и вычитанием целых десятков (20+20=40, 30-20=10), позволяющие ребенку понять, что операции с целыми десятками можно производить так же, как с единицами, если не обращать внимания на ноль.
Этап 3 — основы перехода через десяток
Следующим ключевым моментом является способность ребенка выполнять вычисления, когда результат находится за пределами десятка, в котором они были начаты. Для приучения ребенка к мысли о возможности перехода через десяток сначала ему предлагаются примеры, где от полного десятка нужно отнять несколько единиц (60-2=58). Для ребенка важно научиться отделять один десяток от первого аргумента, запоминать оставшуюся часть, производить вычисления с отделенным десятком, а потом прибавлять получившийся результат к зафиксированному ранее остатку (60-2=(50+10)-2=50+(10-2)=50+8=58).
Далее ребенку предлагаются более сложные примеры, когда либо из неполного десятка нужно вычесть число единиц, превышающее число единиц в уменьшаемом, либо сложить два слагаемых, которые в результате дают число больше 10 (18-9=9, 9+7=16). Одним из самых важных умений на этом этапе является разложение одного из аргументов на две части. Одна часть должна дополнять второй аргумент до полного десятка, а вторая прибавляется или вычитается из полученного полного десятка (18-9=18-8-1=10-1=9, 9+7=9+1+6=10+6=16). Удобно объяснить это ребенку, используя формулировку «прибавить по частям» или «вычесть по частям». Особенно важными являются такие умения в случае вычитания с переходом через десяток. Следует помочь ребенку понять, что можно отделить единицы от десятков и получить из любого двузначного числа пару более простых аргументов, сведя операцию к вычислению с целыми десятками (18-9=10+8-9=10+8-8-1=10-1=9).
Ребенок должен научиться видеть отдельно десятки и единицы, а также вычислять недостающую до целого десятка часть для любого числа от 1 до 9. Очень важно также проследить, чтобы ребенок усвоил переход к вычислениям, содержащим в себе несколько этапов (сперва упрощение, потом финальный результат).
Этап 4 — переход через десяток в пределах 100 (Уроки 16-18)
Четвертый этап представляет собой интенсивное повторение и закрепление материала, усвоенного в рамках первых трех этапов. Ученик тренирует навык сложения и вычитания двузначных и однозначных чисел с переходом через десяток.
Важно осознать, что при этом «лишний» десяток прибавляется к уже имеющемуся количеству десятков в двузначном числе, увеличивая их на 1, а недостающий десяток при вычитании берется также из десятков двузначного числа, при этом количество десятков уменьшается на 1.
Этап 5 — складываем и вычитаем единицы и десятки (Уроки 19-21)
Пятый этап готовит ученика к полноценному сложению и вычитанию двузначных чисел. На этом этапе ученик осваивает действия отдельно с десятками и единицами.
Вначале ученик прибавляет двузначные числа к целым десяткам, либо вычитает двузначные числа из неполных десятков так, чтобы получились целые десятки. Это необходимо, чтобы создать у ученика понимание, каким образом осуществляется переход от неполных десятков к полным при избыточном наполнении (нам нужно отнять несколько единиц, чтобы получить полный десяток) и наоборот (к полному десятку прибавляем несколько единиц и получаем неполный).
Вторая часть этапа тренирует навык сложения и вычитания десятков и единиц по отдельности (перехода через десяток не происходит), поэтому главное, что должен усвоить обучающийся — это складывать и вычитать десятки с десятками, а единицы с единицами.
В заключительной части этапа ученик начинает складывать двузначные числа, получая в результате полные десятки, а также вычитать двузначные числа из полных десятков. Это необходимо, чтобы изучить дополнительно возникающий десяток при сложении (складывая единицы, мы получаем 10), либо метод изъятия целого десятка для того, чтобы было откуда вычитать единицы (сначала производим действия над десятками, затем вычитаем единицы). В том и в другом случае полезно научить ученика сначала складывать или вычитать десятки, затем запоминать промежуточный результат и производить действия над единицами. Объясните ученику, что складывая и вычитая сперва десятки, можно получить примеры из Этапа 4, которые легко решать. Это умение также очень пригодится на следующем этапе.
Этап 6 — полноценное сложение и вычитание двузначных чисел (Уроки 22-25)
На данном этапе ученик складывает и вычитает двузначные числа, состоящие из неполных десятков, с переходом через десяток в результате. Это самый сложный вариант сложения и вычитания двузначных чисел, поскольку требует двухэтапного вычисления (если подходить совсем детально, то можно выделить даже четыре этапа).
Сперва ученик складывает или вычитает отдельно десятки и единицы (эти два действия можно объединить в один этап при более широком подходе). При этом он получает некоторое количество целых десятков и либо число больше 10 (при сложении), либо остаток единиц для вычитания (при вычитании).
Далее при сложении ученик отделяет образовавшийся десяток от единиц и добавляет его к десяткам, затем добавляет к результату единицы. При вычитании ученику приходится дополнительно вычесть оставшиеся единицы из имеющихся у него целых десятков, чтобы получить итоговый результат.
Самой важной задачей ученика является переход именно к двухэтапному вычислению, без излишней детализации. Для этого и производится тренировка сперва примеров на сложение, потом на вычитание, а потом комбинаций таких примеров.
Проблемы и решения
При сложении и вычитании двузначных чисел у учеников возникает две наиболее распространенные проблемы. Они путают десятки и единицы, а также забывают изменить значение десятков в результате, после того, как выполнят действие с единицами, которое при сложении добавляет «лишний» десяток, а при вычитании требует изъять один десяток из результата, чтобы было из чего вычесть оставшиеся единицы вычитаемого.
Путаница с десятками и единицами
Если ученик все равно затрудняется отделять десятки от единиц, мы рекомендуем вернуться ко второму этапу нашего курса «Понятие десятка».
Изменение количества десятков в окончательном результате
Бывает, что ученик записывает в окончательный результат десятки сразу из промежуточного, несмотря на то, что при сложении у него получается еще один десяток после действия над единицами, а при вычитании ему не хватает единиц, и приходится брать дополнительно десяток из промежуточного результата.
В том и в другом случае нужно объяснить ученику, что складывая или вычитая десятки, он получает только промежуточный результат, который надо запомнить, но не писать — из него возможно потребуется что-то еще взять или наоборот, добавить после того, как он проделает действия над единицами. При сложении может получиться еще один десяток, а при вычитании может потребоваться больше единиц, чем у нас есть. Тогда мы и задействуем промежуточный результат — возьмем оттуда недостающее или добавим «лишнее». И только после этого можем записать окончательный результат для десятков, а к нему добавить то, что получилось в единицах.
Уроки и их связь с этапами
Все уроки организованы как комплекс примеров одного вида, позволяя за счет многократного повторения закрепить у ребенка навыки конкретного вида вычислений. Каждый урок закрепляет определенную часть одного из этапов, описанных выше. Введение новых видов вычислений чередуется с закреплением пройденного материала и более сложными вариантами предыдущих уроков. Каждый урок имеет определенную цель, указанную в его описании. Цель данной учебной программы в целом — научить ребенка складывать и вычитать двузначные числа в уме. Важно следить, чтобы ребенок последовательно усваивал элементы вычислений и использовал полученные знания при решении последующих уроков. Критерии оценки включают в себя правильность решения (требуется дать не менее 95% правильных ответов для каждого урока) и среднее время, затрачиваемое на ответ. Среднее время имеет три основных значения — предельно допустимое, нормальное, отличное. Для каждого примера эти значения отличаются, в зависимости от сложности урока и предполагаемого качественного уровня знаний ученика. Переход к следующему уроку предлагается только в том случае, если получено не менее 95% правильных ответов и среднее время меньше предельно допустимого.
Урок 1
Примеры вида 1+5, 8-3 и т.д. Простейшее представление Этапа 1. Ребенок приучается вычислять результат сразу, без прибавления или вычитания по 1. Важно объяснить, что при сложении ребенку будет проще прибавлять меньшее число к большему, а не наоборот (1+5=5+1, при этом 5+1 считать намного удобнее и быстрее). Также важно объяснить, что при вычитании произвольно переставлять аргументы нельзя.
Урок 2
Примеры вида 19-5, 15+4 и т.д. Более сложное представление Этапа 1. Ребенок приучается оперировать единицами в пределах второго десятка. Важно объяснить ему, что первая цифра в двузначных числах такого примера не играет никакой роли, сперва ее можно просто прикрыть пальцем и вычислить результат для однозначных чисел как в Уроке 1, а потом убрать палец, добавить скрытую им цифру и получить правильный ответ. Впоследствии ребенок должен научиться вычислять результат, не прикрывая часть числа, а видя его целиком.
Урок 3
Примеры вида 10+5, 19-9, 19-10 и т.д. В этом примере впервые осуществляется переход к Этапу 2 и вводится понятие десятка, как самостоятельного участника вычислений. Для ребенка важно научиться различать десятки и единицы (сначала возможны ошибки вида 10+5=60, для их коррекции можно воспользоваться приемом, описанным в предыдущем примере). Наибольшее внимание следует уделить операциям с вычитанием целых десятков. Если ребенок испытывает затруднения с вычислениями этого вида, попробуйте научить его прикрывать пальцем сначала первые цифры, а затем вторые — и таким образом получать отдельно десятки, отдельно единицы: 19-10=(1)9-(1)0=(1-1)(9-0)=(0)(9)=09=9. Впоследствии обращайте внимание ребенка на то, что можно просто отбрасывать разряды уменьшаемого и вычитаемого в том случае, если они одинаковые (в примерах этого вида десятки всегда одинаковы).
Урок 4
Примеры вида 20+30, 30-20 и т.д. Операции с целыми десятками, когда десятки складываются и вычитаются так же, как единицы в Уроке 1. Важно объяснить ребенку, что десятки можно складывать и вычитать самостоятельно, и в этом случае они ведут себя точно так же, как единицы — нужно только потом не забывать добавлять 0 справа к полученному результату.
Урок 5
Примеры вида 27+1, 27-1 и т.д. Закрепление пройденного материала. Одновременно происходит повторение присчитывания к различным числам и закрепление понимания того, что единицы внутри любого десятка ведут себя так же, как и внутри первого (27+1=20+(7+1)=20+8=28). Ребенок готовится к тому, чтобы производить вычисления внутри десятков, получая результаты с неполными десятками.
Урок 6
Примеры вида 52+4, 58-5 и т.д. Вычисления, аналогичные Уроку 2, но производящиеся внутри различных десятков. Таким образом, ребенок приучается к тому, что в пределах любого десятка одинаковые единицы ведут себя совершенно одинаково, важно показать и объяснить ему связь с Уроками 1 и 2.
Урок 7
Примеры вида 60-2, 50-4 и т.д. Первое упражнение с переходом через десяток (переход к Этапу 3). Очень важно научить ребенка отделять один десяток от остальных и объяснить ему, что от 10 отнимать несколько единиц он уже умеет, а остальные десятки нужно потом просто прибавить к получившимся единицам, и это он тоже уже умеет делать (Урок 7 тесно связан с Уроками 1, 3, 4).
Урок 8
Примеры вида 18-9, 16-8 и т.д. Более сложный вариант перехода через десяток. Нужно показать ребенку связь с Уроками 3 и 7 и научить сперва вычитать единицы, а потом остаток из целых десятков (18-9=18-8-1=10-1, 16-8=16-6-2=10-2).
Урок 9
Примеры вида 9+7, 8+5 и т.д. Вариант перехода через десяток в большую сторону. Важно научить ребенка видеть недостающую до десятка часть слагаемого (9+7=9+1+6=10+6) и показать связь с Уроками 1 и 3.
Урок 10
В этом примере сочетаются Уроки 8 и 9 для окончательного закрепления навыков вычисления с переходом через десяток. Если ребенок испытывает затруднения с этим уроком, следует вернуться к Урокам 8 и 9 по отдельности для закрепления навыков. При этом следует уделить больше внимания объяснению ребенку связей с предыдущими Уроками.
Урок 11
Примеры вида 20+6, 26-20, 26-6. Этот урок связан с Уроком 3 так же, как Урок 6 связан с Уроками 1 и 2. Следует показать ребенку эту связь и приучить его к мысли, что с десятками, так же, как и с единицами в пределах любого десятка, можно оперировать однотипно.
Урок 12
Примеры вида 56+4, 63+7 и т.д. Разновидность Этапа 3, переход через десяток осуществляется вверх до целого десятка. Важно показать ребенку связь с Уроками 3, 7, 9 и объяснить, по какому принципу единицы переходят в десятки (когда сумма единиц равна 10, мы получаем плюс один десяток).
Урок 13
Примеры вида 34+20, 34+2 и т.д. Важно проследить, чтобы ребенок четко различал понятия десятков и единиц, прибавляя десятки к десяткам, а единицы к единицам. В случае совершения большого количества ошибок нужно показать ребенку связь с Уроками 4 и 6, при необходимости вернуться к закреплению материала этих уроков.
Урок 14
Примеры вида 48-30, 48-3 и т.д. Важно проследить, чтобы ребенок вычитал десятки из десятков, а единицы из единиц. Покажите ребенку связь с Уроком 13, объясните, что эти уроки отличаются только знаком (плюс или минус), а в остальном совершенно одинаковы. При необходимости вернитесь к Уроку 13, либо к Урокам 4 и 6.
Урок 15
Последний урок представляет собой сочетание примеров из Уроков 13 и 14. Ребенок должен хорошо различать не только десятки и единицы, но также и вид вычисления — сложение или вычитание. При необходимости дополнительного повторения вернитесь к Урокам 13 и 14.
Урок 16
Примеры вида: 55+7, 89+4 — тренировка перехода вперед через десяток.
Для ученика важно усвоить, что переход вперед через десяток осуществляется одинаково, независимо от десятка, из которого мы начали движение. Количество десятков при этом увеличивается на 1.
Урок 17
Примеры вида: 51-8, 22-4 — тренировка перехода назад через десяток. Так же, как и в Уроке 16, самым важным является понимание, что переход через десяток осуществляется одинаково, независимо от десятка, из которого мы начали движение. Количество десятков при этом уменьшается на 1, а остаток единиц вычитаемого вычитается из целых десятков.
Важно не забывать вычесть остаток единиц.
Урок 18
Примеры вида: 55+7, 51-8 — тренировка перехода вперед и назад через десяток. Сочетание Уроков 16 и 17, важно сохранять правильное направление движения в зависимости от знака действия «+» или «-».
Урок 19
Примеры вида: 40+16, 36-16 — первый опыт действий с двузначными числами. Важно сразу же начать складывать и вычитать сначала десятки, потом единицы.
Необходимо следить, чтобы ученик запоминал промежуточный результат для десятков, пока проделывает действия с единицами, и не забывал добавлять его к итоговому результату. Лучше, чтобы ученик именно запоминал промежуточный результат, а не писал его сразу — это поможет на следующих этапах.
Урок 20
Примеры вида: 45+12, 45-12 — несколько усложненный вид Урока 19. Нужно производить действия и над десятками, и над единицами, запоминать результаты и потом составлять из них итоговый ответ.
Данный урок является необходимым для перехода к полноценному сложению и вычитанию двузначных чисел.
Урок 21
Примеры вида: 58+22, 40-16 — несмотря на то, что урок кажется похожим на Урок 19, это не так. В данном уроке впервые появляются «лишние» десятки при сложении и ощущается недостаток единиц в уменьшаемом при вычитании.
Ученик должен научиться производить дополнительные действия с промежуточным результатом для десятков — добавить к нему получившийся «лишний» десяток при сложении единиц или взять из него недостающий десяток при вычитании. Важно запоминать не только промежуточный результат действий над самими десятками, но и то, что мы добавили или взяли один десяток из этого результата.
Урок 22
Примеры вида: 17+19, 35+57 — полноценное сложение двузначных чисел с переходом через десяток. У нас получается не только «лишний» десяток при действиях с единицами, но мы еще и имеем дело с неполными десятками при действиях над единицами. Нужно не только сначала сложить десятки, затем учесть появившийся «лишний» десяток и прибавить его к промежуточному результату, но еще и добавить к этому результату оставшиеся при сложении единицы.
Ученику важно держать в уме сразу три позиции: промежуточный результат по десяткам, дополнительный десяток при сложении единиц, оставшиеся при сложении единицы — и только сложив все три позиции вместе, записывать итоговый результат.
Урок 23
Примеры вида: 62-36, 82-15 — полноценное вычитание двузначных чисел с переходом через десяток. Один из самых сложных видов действий с двузначными числами, поскольку требует правильной последовательности при получении итогового результата. Сперва ученик должен вычесть десятки и запомнить промежуточный результат для них. Затем он должен взять недостающий десяток из этого промежуточного результата и запомнить для десятков уменьшенное на 1 значение. Затем, взяв десяток и добавив к нему единицы уменьшаемого, из получившегося числа должен вычесть единицы вычитаемого. И получившиеся в результате единицы добавить к промежуточному результату для десятков.
Альтернативным решением является вычитание единиц по частям, хотя в конечном итоге такой подход не дает особого выигрыша в количестве или сложности действий.
Урок 24
Примеры вида: 17+19, 62-36 — сочетание Уроков 22 и 23. Для ученика важно не путать направление движения и последовательность действий для сложения и вычитания.
При проблемах с данным Уроком можно вернуться и повторить Уроки 22 и 23 по отдельности, либо только те действия, с которыми возникают проблемы.
Урок 25
Сложение и вычитание любых двузначных чисел с результатом в пределах 100. Важно, чтобы ученик ориентировался, когда необходим переход через десяток, а когда он не нужен. Также важно удостовериться, что ученик производит действия над десятками и единицами правильно.
Детям / Ученикам
Сложение и вычитание до 10
Ты уже знаешь числа от 0 до 10, знаешь, какие из них больше, какие меньше. Ты знаешь, что каждое число можно получить, прибавив 1 к предыдущему (1+1=2). Или вычитая 1 из следующего (5-1=4). Теперь нужно научиться складывать и вычитать числа больше 1.
Сложение
Сложение двух чисел больше 1 значит, что нужно к одному из них столько раз прибавить по 1, сколько единиц содержит второе число. Например: 5+3 = 5+(3 раза по 1) = 5+1+1+1.
Получается, что мы увеличиваем число несколько раз на 1, и нам нужно прибавить только 1 каждый раз, а это мы уже умеем делать. 5+1+1+1=6+1+1=7+1=8. Получается, что мы можем решить пример 5+3=8, прибавляя только по 1 несколько раз. Числа 5 и 3 в этом примере называются слагаемое (оба они называются при сложении одинаково), а число 8 называется сумма. Потом, когда ты будешь хорошо знать, как решать эти примеры, ты сразу будешь давать правильный ответ, не прибавляя единицы, а сразу получая сумму в уме.
При сложении важно знать, что результат не изменится даже если ты переставишь слагаемые местами. Давай проверим:
5+3 = 5+1+1+1 = 6+1+1 = 7+1 = 8
3+5 = 3+1+1+1+1+1 = 4+1+1+1+1 = 5+1+1+1 = 6+1+1 = 7+1 = 8
Как видишь — сумма не меняется. Но посмотри, насколько длиннее получился второй пример! А если ты посмотришь внимательно, то увидишь, что когда мы решали пример 3+5, мы прибавили к 3 две единицы из 5 и получили пример 5+3. Поэтому удобнее всегда прибавлять к большему числу меньшее. Если ты видишь пример 3+5 или 2+7 — смело переставляй слагаемые местами. 5+3 или 7+2 решать намного быстрее и проще, а сумма будет такая же.
Вычитание
Вычитание двух чисел больше 1 значит, что из первого из них нужно вычесть по 1 столько раз, сколько единиц содержит второе число. Например: 8-3=8-(три раза по 1)=8-1-1-1.
Получается, что мы уменьшаем число несколько раз на 1, и нам нужно вычесть только 1 каждый раз, а это мы уже умеем делать. 8-1-1-1=7-1-1=6-1=5. Получается, что вычитая только по 1 несколько раз, мы можем решить пример 8-3=5. Число 8 в этом примере называется уменьшаемое (его мы делаем меньше, уменьшаем), число 3 называется вычитаемое (его мы вычитаем из 8, чтобы уменьшить уменьшаемое), а число 5 называется разность (оно показывает разницу между уменьшаемым и вычитаемым).
В отличие от сложения, переставлять местами уменьшаемое и вычитаемое при вычитании нельзя. Уменьшаемое — самое большое число в примере, если мы переставим его на место вычитаемого — мы не сможем решить пример. Давай проверим:
8-3 = 8-1-1-1 = 7-1-1 = 6-1 = 5
3-8 = 3-1-1-1-1-1-1-1-1 = 2-1-1-1-1-1-1-1 = 1-1-1-1-1-1-1 = 0-1-1-1-1-1
Видишь? Мы не можем вычитать дальше, потому что не умеем вычитать из нуля! Поэтому менять местами уменьшаемое и вычитаемое нельзя.
Потом, когда ты научишься хорошо вычитать, тебе уже не нужно будет каждый раз вычитать из уменьшаемого по единице, ты сразу будешь получать разность в уме, как только увидишь уменьшаемое и вычитаемое.
Что такое десяток
Десять единиц — десяток
Ты уже знаешь числа от 0 до 9 и знаешь, что бывают числа больше 9 (например, 10). Посмотри внимательно на число 10 — чем оно отличается от всех других чисел от 0 до 9? Правильно, в нем две цифры. Прибавив к 9 единицу, мы получаем первый десяток. Он обозначается, как 1 (первый), написанная слева от 0 (в десятке пока ноль единиц). Числа от 0 до 9 называются единицами (помнишь, мы прибавляем по единице, чтобы получить следующее число?). Каждая единица увеличивает эти числа на 1. А для того, чтобы увеличить на 1 десяток, нам нужно целых 10 единиц. Десяток — это десять единиц.
Десятки нужны нам потому, что у нас всего десять разных цифр, и мы не можем по-другому записать числа больше 9. Если бы не придумали десятки, нам потребовалось бы для 10 придумывать свою цифру (1 и 0 использовать было бы уже нельзя), для 11 — еще одну, и все их запоминать. Десяток позволяет нам начать считать как бы «с начала», записать, сколько десятков у нас есть — и снова считать единицы от 0 до 9. Десять единиц — один десяток. Двадцать единиц — два десятка. Посмотри — десятки мы считаем так же, как единицы, только вместо 1 прибавляем сразу 10. Если закрыть вторую цифру пальцем в числах 10, 20, 30, 40 — увидишь уже знакомые тебе числа 1, 2, 3, 4. Это и есть десятки — один десяток, два десятка, три десятка, четыре десятка. Видишь — они очень похожи на единицы. Их так же считают от 0 до 9. Когда ты считаешь числа от 0 до 9, у тебя есть ноль десятков и несколько единиц. То есть десятки есть в любом числе — просто пока число меньше 10, десятков в нем ноль (любое число от 0 до 9 можно записать как 00, 01, 02, 03, 04. ). Когда число становится равно 10, в нем появляется один десяток и ноль единиц. Мы пишем 1 слева от единиц (чтобы не забыть, что у нас уже есть один десяток) — и продолжаем считать единицы дальше (10+1=11, 11+1=12, 12+1=13, 13+1=14. ). Когда насчитаем еще 10 единиц — прибавляем еще один десяток (19+1=10+9+1=10+10=20). Теперь у нас уже два десятка и снова ноль единиц. Теперь уже слева от единиц мы пишем 2, а единицы начинаем считать снова с нуля (20+1=21, 21+1=22, 22+1=23, 23+1=24. ).
Иногда нам нужно вычесть несколько единиц из числа больше 10. Тогда мы тоже вычитаем единицы из единиц, а десяток так и остается записанным слева. 15-2=13, 18-1=17, 16-4=12.
Считаем десятки
Как только ты поймешь, как получаются десятки — тебе будет очень легко считать их. Представь, что мы складываем в кучу шарики. В кучу у нас может влезть только 10 шариков, потом она будет разваливаться. Поэтому мы складываем 10 шариков в кучу и больше туда ничего не кладем, а начинаем складывать рядом вторую кучу. Первая куча — это и есть десяток. Мы его как бы отложили в сторону и начали складывать рядом новую кучу из единиц — шариков. Получим еще одну кучу из 10 шариков — у нас будет два десятка, оба лежат рядом, и если нам понадобятся шарики из них — мы их можем взять. Мы складываем новую кучу, но все целые кучи никуда не делись — они остаются тут же под рукой. Теперь начинаем собирать шарики, чтобы сложить их обратно в коробку. Сначала мы берем шарики из кучи с единицами (сначала разбираем неполную кучу, чтобы не трогать наши красивые ровные десятки), а когда они там кончатся — начинаем брать из десятков. Как только мы взяли хотя бы один шарик из десятка — у нас снова получились единицы (куча стала неполной), а десятков (полных куч) стало меньше на 1. Десяток — это ровно 10 единиц, ни больше, ни меньше.
Сколько у тебя есть куч по 10 шариков — столько у тебя десятков. Если считать не шарики, а кучи, то можно говорить не 10, 20, 30 шариков, а один, два, три десятка шариков. Видишь, десятки можно считать так же, как единицы — от 0 до 9. И кучи (десятки) можно двигать целиком. Если взять две и три кучи шариков — у нас получится 20 и 30 шариков или 2 и 3 десятка шариков. Теперь возьмем и составим все кучи рядом — у нас получится 5 куч или 5 десятков шариков или 50 шариков. Видишь, как просто можно складывать десятки? 20 и 30 можно сложить так же легко, как 2 и 3. Нужно просто не обращать внимания на ноль в конце чисел 20 и 30, а складывать 2 и 3 десятка. Получим 5 десятков, а потом вспомним про ноль, допишем его — и получим 50. 20+30=50.
А теперь возьмем получившиеся пять куч и отделим обратно наши две кучи. Было пять куч — стало снова три и две. Унесем две кучи — останется только три. Было 5 десятков шариков, унесли (вычли) 2 десятка, осталось 3 десятка. Было 50 шариков, унесли 20, осталось 30. Вычитать десятки мы можем так же, как единицы, нужно просто считать левые части чисел, а про ноли пока забыть. Вычесть 20 из 50 так же легко, как вычесть 2 из 5. Берем 5 десятков и вычитаем из них 2 десятка. Получаем 3 десятка. Теперь вспоминаем про ноль и дописываем его — получаем 30. 50-20=30.
Десятки нужны для того, чтобы удобно было записывать числа больше 9. Десятки можно складывать и вычитать так же, как единицы.
Десятки и единицы вместе
Остаток от десятка
Если единиц больше 10 — мы будем писать остаток в «свободную» часть десятка, там где у нас был ноль (10 становится 11, потом 12, 13 и так далее). Это очень легко, нужно просто запомнить, что единицы мы пишем в самую правую часть числа, туда, где у десятков стоят нули. 10+5=15, 20+3=23, 30+8=38 — правда, все просто?
Если же нам нужно вычесть несколько единиц из десятка — мы вычитаем 1 из десятков и получаем 10 единиц, из которых можем вычесть нужное нам количество, а остаток записать в единицы. Ты уже умеешь вычитать из 10 любые числа от 0 до 9, верно? Так же точно можно вычитать числа от 0 до 9 из любого десятка — из 20, 30, 40 и так далее. Нужно просто отделить один десяток (10 единиц) и вычитать из него. Только не забудь уменьшить число десятков на 1 — ты же отделяешь один десяток. 20 превращается в 10, 30 в 20, 40 в 30. А остаток от вычитания мы пишем в «свободную» часть числа вместо ноля. Например, если нам нужно вычесть 6 из 40, мы отделяем один десяток (вместо 40 получаем 30 и 10), 30 пока откладываем в сторону, а из 10 вычитаем 6. Получается 30 и 4. Вместо ноля к 30 мы запишем 4 и получаем число 34 — это и есть разность 40 и 6.
Переход через десяток
Иногда бывает так, что результат нельзя получить сразу. Например, как прибавить 5 к 8? Сразу и не скажешь, сколько получится, верно? Больше 10, а вот как посчитать, сколько именно? Давай попробуем разбить результат на десятки и единицы. Десятки ты уже умеешь получать, для этого нам нужно получить ровно 10, ни больше, ни меньше. Чтобы получить 10, нам нужно разбить число 5 на части. Сколько нужно прибавить к 8, чтобы получить 10? Правильно, 2. Заберем 2 из 5 и прибавим к 8. Получим 10, а от 5 у нас останется только 3. Теперь у нас есть десяток и три единицы. Сложить их очень легко, 10+3=13. Получается, что 8+5=8+2+3=10+3=13.
Точно так же мы будем поступать, когда нам нужно вычесть из числа с десятками вычитаемое, которое больше количества единиц в уменьшаемом. То есть, например, из 32 вычесть 6. Сразу непонятно, сколько получится, правда? Вот если бы было 30 — это мы уже умеем делать. Давай получим сначала 30 из 32. Для этого нам надо разбить 6 на части — сколько нужно вычесть из 32, чтобы осталось 30? 2, верно? Из 6 забираем 2, остается 4. Из 32 вычитаем 2, остается 30. Теперь у нас осталось 30, а вычесть из них надо уже не 6, а только 4 (два мы забрали, помнишь?). Теперь от 30 нужно отделить один десяток, из которого мы и будем вычитать. У нас есть три десятка, если отделить один, то останется еще два. Получается, что из 30 мы возьмем 10, а еще 20 останется, потом добавим их к результату. Из 10 вычесть 4 — будет 6. Получили 6, да еще 20, которые оставались — будет 26. Получается, что 32-6=32-2-4=30-4=20+10-4=20+6=26. Совсем не трудно, правда?
Это интересно: порядки
Такая запись, когда десятки пишутся слева от единиц, сотни слева от десятков и так далее, в математике называется порядками. Единицы — числа первого порядка, десятки — второго порядка. Потом ты будешь изучать третий, четвертый, пятый порядки — их очень много, но все они пишутся так же, как десятки — слева от числа. Если ты посчитаешь, сколько цифр в числе — ты сможешь сказать, сколько в нем порядков. Одна цифра — один порядок, единицы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 — это все единицы, числа первого порядка. Две цифры — два порядка, десятки: 23, 48, 14, 56 — это примеры чисел второго порядка. Три цифры — три порядка, сотни: 100, 123, 554. И так далее. В числа первого порядка входят только единицы, в числа второго порядка входят десятки и единицы, в числа третьего порядка — сотни, десятки и единицы, то есть каждый порядок включает в себя все предыдущие.
Сложение и вычитание двузначных чисел
Ты уже умеешь складывать и вычитать однозначные числа, а также прибавлять и вычитать однозначные числа из двузначных. Ты даже умеешь переходить при этом через десяток. Теперь тебе осталось научиться складывать и вычитать двузначные числа — и ты будешь знать все способы сложения и вычитания до 100. Чтобы научиться этому, потребуется три этапа.
Переход через десяток в пределах 100 (Уроки 16-18)
Cкладывае и вычитаем единицы и десятки (Уроки 19-21)
Теперь задача немного сложнее. Тебе нужно не просто прибавить несколько единиц к двузначному числу или вычесть их из него, а еще и прибавить или вычесть десятки. Чтобы тебе было проще — сначала прибавляй или вычитай десятки, а потом единицы. Видишь, как похоже получается задание на примеры из первых уроков, если сначала прибавить или вычесть десятки? Всегда проще сначала выполнять действия с более высокими порядками, потом с более низкими.
Полноценное сложение и вычитание двузначных чисел (Уроки 22-25)
Примеры и их решение
Сложение и вычитание до 10
Сложение
3+6=6+3=6+1+1+1=7+1+1=8+1=9, 3 и 6 — слагаемые, 9 — сумма
Вычитание
9-1=8, 9 — уменьшаемое, 1 — вычитаемое, 8 — разность
6-4=6-1-1-1-1=5-1-1-1=4-1-1=3-1=2, 6 — уменьшаемое, 4 — вычитаемое, 2 — разность
Действия с десятками
Сложение
20+30=50, 2, 3, 5 — десятки, 0 — единицы
Вычитание
50-20=30, 2, 3, 5 — десятки, 0 — единицы
Действия с десятками и единицами
Сложение с переходом через десяток
8+6=8+2+4=10+4=14, 6 прибавляем по частям, чтобы из 8 сначала получить 10, а потом добавить остаток от 6
25+9=25+5+4=30+4=34, 9 прибавляем по частям, чтобы сначала из 25 получить 30, а потом добавить остаток от 9
8+13=13+8=13+7+1=20+1=21, сначала переставляем местами слагаемые, чтобы к большему прибавлять меньшее. Потом прибавляем 8 по частям, чтобы сначала из 13 получить 20, а потом добавить остаток от 8
Вычитание с переходом через десяток
30-4=20+10-4=20+6=26, сначала отделяем один десяток от 30, из него вычитаем единицы, а потом прибавляем полученные единицы к 20, оставшимся от 30 после отнятия десятка
23-6 = 23-3-3 = 20-3 = 10+10-3 = 10+7 = 17, сначала разбиваем 6 на части, чтобы из 23 получить 20, а потом из 20 вычитаем остаток от 6. Для этого мысленно от 20 отделяем один десяток и считаем, сколько от него останется единиц, если вычесть 3. Полученные единицы прибавляем к 10, оставшимся от 20 после отнятия десятка
Сложение и вычитание с участием целых десятков
Примеры вида: 40+16, 36-16 — первые действия с двузначными числами.
Запомни — сначала складываем или вычитаем десятки, потом единицы. Так ты не запутаешься, и потом будет гораздо проще. Если ты сложишь или вычтешь сначала десятки — то получится знакомый тебе пример из Уроков 1-3, где надо сложить или вычесть промежуточный результат и несколько единиц, а такие ты уже умеешь решать.
40+16 = 40+10+6 = 50+6 = 56
36-16 = 30+6-10-6 = 30-10+6-6 = 20+0 = 20
Простое сложение и вычитание двузначных чисел
Примеры вида: 45+12, 45-12 — похоже на Урок 4, но в обоих числах присутствуют и десятки, и единицы. Нужно просто складывать или вычитать их по отдельности, а потом сложить промежуточные результаты (десятки и единицы), чтобы получить итоговый результат.
45+12 = 40+5+10+2 = 40+10+5+2 = 50+7 = 57
45-12 = 40+5-10-2 = 40-10+5-2 = 30+3 = 33
Основы перехода через десяток с двузначными числами
Примеры вида: 58+22, 40-16 — эти примеры похожи на Урок 4, но обрати внимание, что в них есть переход через десяток.
Сначала мы так же, как и в Уроках 4 и 5, складываем или вычитаем десятки. А потом смотрим, что нужно сделать с единицами. Если мы складываем их, обрати внимание, что в результате получится целый десяток. Его нужно будет прибавить к десяткам промежуточного результата, а не к единицам. Если же мы вычитаем единицы — то нам не хватит единиц в уменьшаемом. Придется взять один десяток из промежуточного результата (уменьшить десятки в промежуточном результате на 1), а потом добавить к нему оставшиеся после вычитания единицы, чтобы получить итоговый результат.
58+22 = 50+8+20+2 = 50+20+8+2 = 70+10 = 80
40-16 = 40-10-6 = 30-6 = 20+10-6 = 20+4 = 24
Действия с двузначными числами с переходом через десяток
Сложение двузначных чисел с переходом через десяток
Примеры вида: 17+19, 35+57 — самый сложный вариант сложения двузначных чисел.
Оба числа двузначные, да еще и единиц столько, что придется делать переход через десяток. Но ты уже знаешь, как решать такие примеры. Сначала складываем десятки, запоминаем промежуточный результат. Потом складываем единицы по частям, полученный десяток прибавляем к промежуточному результату, а потом добавляем оставшиеся единицы и получаем итоговый результат.
35+57 = 30+5+50+7 = 30+50+5+7 = 80+12 = 80+10+2 = 90+2 = 92
Вычитание двузначных чисел с переходом через десяток
Примеры вида: 62-36, 82-15 — самый сложный вариант вычитания двузначных чисел.
Сначала вычитаем десятки, запоминаем промежуточный результат. Потом вычитаем единицы по частям. Когда единицы в уменьшаемом кончатся, возьмем из промежуточного результата один десяток, вычтем из него остаток единиц. Количество десятков в промежуточном результате уменьшим на 1, а потом добавим оставшиеся единицы, чтобы получить итоговый результат.
62-36 = 60+2-30-6 = 60-30+2-6 = 30-4 = 20+10-4 = 20+6 = 26
Помощь
Элементы управления
Верхнее меню
Элементы управления (навигации), находящиеся в верхнем меню. Они представлены в виде картинок (иконок). Часть из них будут постоянно находится в меню, а часть появляться на тех страничках, для которых они необходимы.
Элементы управления для отдельного урока (в списке уроков)
Об учебном процессе
Прежде, чем вы начнете
Обучение пойдет намного быстрее, если уроки проходить по порядку. В каждом уроке отрабатывается 1-2 навыка необходимых ребенку для легкого и быстрого сложения и вычитания двузначных чисел в уме. Каждый урок предполагает уже усвоенные навыки из предыдущих уроков.
Описание учебного процесса
Курс для обучения сложению и вычитанию двухзначных чисел в уме.
На протяжении всего курса необходимо решать примеры на сложение и вычитание. Курс разбит на уроки по тематикам и степени сложности.
На главной странице курса представлен список из 25 уроков. Требуется решать примеры достаточно правильно (количество правильных ответов должно быть не менее 95%) и быстро (в зависимости от сложности примеров, каждый ответ должен занимать в среднем не более 3-6 секунд), чтобы завершить урок.
Будут показаваться примеры, нужно вводить ответ с помощью клавиатуры.
Если ответ правильный, производится переход к следующему примеру. В случае неверного ответа показывается сообщение об ошибке и выводится правильный ответ.
Учитываются ошибки и время, за которое дан правильный ответ.
Для завершения урока необходимо решить не менее 100 примеров, но необходимое количество будет корректироваться в зависимости от количества ошибок и времени за которое дан правильный ответ (если оно больше допустимого).
Над примером расположена шкала (прогресс), показывающая, сколько процентов от полного материала урока пройдено.
Урок завершен, когда процент готовности по уроку 100%. В списке уроков этот урок помечается так
Через каждые 10 примеров тренажер переходит в режим «Паузы». Это необходимо чтобы отдохнуть и отвлечься, т.к. важно время, затраченное на пример. Здесь же ученику сообщается о том, насколько хорошо он справляется с заданием: в таблице приведены показатели текущей успеваемости по последней группе примеров — количество правильных ответов, ошибок, среднее время, затрачиваемое на ответ, а также среднее время, необходимое для того, чтобы материал считался усвоенным. Если среднее время ученика меньше указанного (в этом случае оно будет зеленым) — значит все в порядке.
После паузы можно продолжить или вернуться к списку уроков. При этом прогресс по уроку будет сохранен.