Операции над машинными кодами чисел
Все современные ЭВМ имеют достаточно развитую систему команд, включающую десятки и сотни машинных операций. Однако выполнение любой операции основано на использовании простейших микроопераций типа сложения и сдвиг. Это позволяет иметь единое арифметико-логическое устройство для выполнения любых операций, связанных с обработкой информации. Правила сложения двоичных цифр двух чисел А и В представлены в табл. 1.4.
Здесь показаны правила сложения двоичных цифр ai, bi одноименных разрядов с учетом возможных переносов из предыдущего разряда pi-1.
| Значения разрядов двоичных чисел а и b | Разряд суммы Si | Перенос в следующий разряд Рi |
| ai | bi | pi-1 |
• во-первых, приходится отдельно обрабатывать значащие разряды чисел и разряды знака;
• во-вторых, значение разряда знака влияет на алгоритм выполнения операции (сложение может заменяться вычитанием и наоборот).
Во всех ЭВМ без исключения все операции выполняются над числами, представленными специальными машинными кодами. Их использование позволяет обрабатывать знаковые разряды чисел так же, как и значащие разряды, а также заменять операцию вычитания операцией сложения.
Сложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код. Пусть числа А≥0 и В≥0, тогда операция алгебраического сложения выполняется в соответствии с табл. 1.5.
Таблица преобразования кодов при алгебраическом сложении
Скобки в представленных выражениях указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа. Сложение двоичных чисел осуществляется последовательно, поразрядно в соответствии с табл. 1.4. При выполнении сложения с использованием машинных кодов необходимо соблюдать следующие правила.
1. Слагаемые должны иметь одинаковое число разрядов. Для выравнивания разрядной сетки слагаемых можно дописывать нули слева к целой части числа и нули справа к дробной части числа.
2. Знаковые разряды чисел участвуют в сложении так же, как и значащие.
3. Необходимые преобразования кодов (п.1.2.) производятся с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу.
4. При образовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом. При использовании ДК единица переноса отбрасывается. Знак результата формируется автоматически, результат представляется в том коде, в котором представлены исходные слагаемые.
Пример 1.17. Сложить два числа А10=7 В10=16
Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки:
Сложение в обратном или дополнительном коде дает один и тот же результат 0.00111
Обратим внимание, что при сложении цифр отсутствуют переносы в знаковый разряд и из знакового разряда, что свидетельствует о получении правильного результата.
В соответствии с табл. 1.5 должна быть реализована зависимость А+(-В), в которой второе слагаемое преобразуется с учетом знака
[A2]пк = 0.10000 = 0.10000 [А2]ок = 0.10000 [А2]дк = 0.10000;
[B2]пк = 1.00111 = 1.00111 [В2]ок = 1.11000 [В2]дк = 1.11001.
Сложение в OK Сложение в ДК
При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда. В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда (см.п.4 правил). В случае ДК этот перенос игнорируется.
Пример 1.19. Сложить два числа А10 =- 16 В= +7 в ОК и ДК.
В соответствии с табл. 1.3 должна быть реализована зависимость
(-А)+В, в которой первое слагаемое преобразуется с учетом знака
[B2]пк = + 00111= 0.00111 [В2]ок = 0.00111 [В2]дк = 0.00111.
Сложение в OK Сложение в ДК
При сложении чисел в ОК и ДК были получены отрицательные результаты («1» в знаковом разряде). Для перевода обратного кода отрицательного числа в прямой необходимо инвертировать значащие разряды, а знаковый разряд оставить без изменения. А для перевода дополнительного кода отрицательного числа в прямой код необходимо инвертировать значащие разряды и прибавить единицу младшего разряда.
т.о. имеем в ПК из ОК 1.01001, а в ПК из ДК 1.01000
Умножение. Умножение двоичных чисел реализуется в прямом коде. Рассмотрим, каким образом оно приводится к операциям сложения и сдвигам.
Перемножим эти числа, представленные прямыми двоичными кодами, так же, как это делается в десятичной системе.
+ 111 – мл. разряд ОП2 равен «1», поэтому к РЧС +ОП1;
1 такт å = 111 – результирующее значение РЧС;
® 0111 – сдвиг РЧС вправо на один разряд;
2 такт å = 00111 –очередной р-д ОП2=«0», поэтому только сдвиг
Знак произведения определяется путем сложения по «модулю 2» знаков сомножителей ( 0 Å 0 = 0)
Нетрудно видеть, что произведение получается путем сложения частных произведений, представляющих собой разряды множимого, сдвинутые влево в соответствии с позициями разрядов множителя. Частные произведения, полученные умножением на нуль, игнорируются. Важной особенностью операции умножения n-разрядных сомножителей является увеличение разрядности произведения до п+п=2п. Знак произведения формируется путем сложения по модулю «2» знаковых разрядов сомножителей. Возможные переносы из знакового разряда игнорируются.
Деление. Операция деления, как и в десятичной арифметике, является обратной операции умножения. Эта операция также приводится к последовательности операций сложения и сдвига.
Отметим, что делимое перед операцией деления должно быть приведено к 2n-разрядной сетке. Только в этом случае при делении на n-разрядный делитель получается n-разрядное частное.
Знак частного формируется также путем сложения по «модулю 2» знаковых разрядов делимого и делителя, как это делалось при умножении.
Признаками переполнения являются:
n наличие переноса из значащих разрядов в знаковый и отсутствие переноса из знакового разряда («положительное» переполнение);
n наличие переноса из знакового разряда и отсутствие переноса из значащих в знаковый разряд («отрицательное» переполнение).
Пример 1.21.Сложить 2 числа: А=+5 и В=+6 в четырехразрядной сетке (с учетом знакового разряда).
Сложение в OK Сложение в ДК
Пример 1.22.
Сложить 2 числа: А=-5 и В=-6 в четырехразрядной сетке (с учетом знакового разряда).
Сложение в OK Сложение в ДК
Как видно из примеров, при сложении положительных чисел получается отрицательный результат и наоборот. Это объясняется тем, что в трех значащих разрядах максимальное число по модулю может быть семь, а в примерах необходимо записать соответственно С=+11 и С=-11.
Задания для работы на занятии:
1.Перевести из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную и двоично-десятичную числа:
-175,34;
-256,75.
2.Перевести из двоичной системы счисления в десятичную, восьмеричную, шестнадцатеричную и двоично-десятичную числа:
-10000111010101,1001;
-1111100010101111100101,10101.
3. Образовать все виды машинных кодов от чисел:
4.Умножить в машинных кодах числа:
-5 и +9;
-3 и –8.Результат проверить.
Контрольные вопросы:
1. Что понимается под системой счисления?
2. Сформулируйте правила перевода целых и дробных чисел из одной системы счисления в другую?
3. Как переводятся числа в системах счисления с основаниями, кратными степени 2?
4. Каково назначение обратного и дополнительного кодов?
5. Каково назначение модифицированных обратного и дополнительного кодов?
Задание на самоподготовку:
1. Составить и выполнить по одному примеру на решение задач по
· переводу чисел из одной системы счисления в другую;
· образованию машинных кодов;
· их сложению, вычитанию и умножению.
2. Подготовиться к ПЗ№2 «Минимизация логических функций».
Литература:
1. Пятибратов А.П. и др. Вычислительные системы, сети и телекоммуникации: Учебник.-2-е изд., перераб. и доп./ А.П.Пятибратов, Л.П. Гудыно, А.А.Кириченко; Под ред. А.П.Пятибратова. М.: Финансы и статистика, 2002.-512с:ил.
2. Каган Б.М. Электронные вычислительные машины и системы: Учеб. Пособие для вузов.-3-е изд.,перераб и доп.-М.: Энергоатомиздат,1991.-592с.:ил.
3. Нешумова К.А. Электронные вычислительные машины и системы. М.: Высшая школа, 1989.-366с.:ил.
5. Арифметические операции в ЭВМ
Все современные ЭВМ имеют достаточно развитую систему команд, включающую десятки и сотни машинных операций. Однако выполнение любой операции основано на использовании простейших микроопераций типа сложения и сдвиг. Это позволяет иметь единое арифметико-логическое устройство для выполнения любых операций, связанных с обработкой информации. Правила сложения двоичных цифр двух чисел А и В представлены в табл. 2.
Здесь показаны правила сложения двоичных цифр ai, bi одноименных разрядов с учетом возможных переносов из предыдущего разряда pi-1.
Правила сложения двоичных цифр
Перенос в следующий разряд
• • во-первых, следует отдельно обрабатывать значащие разряды чисел и разряды знака;
• • во-вторых, значение разряда знака влияет на алгоритм выполнения операции (сложение может заменяться вычитанием и наоборот).
Во всех ЭВМ без исключения все операции выполняются над числами, представленными специальными машинными кодами. Их использование позволяет обрабатывать знаковые разряды чисел так же, как и значащие разряды, а также заменять операцию вычитания операцией сложения,
Различают прямой код (П), обратный код (ОК) и дополнительный код (ДК)
5.1. Машинные коды
Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (нуль или единица) перед его старшим числовым разрядом.
A 10 =+10 A 2 =+1010 [A 2 ] П =0:1010;
B 10 =-15 B 2 =-1111 [B 2 ] П =1:1111.
Точечной вертикальной линией здесь отмечена условная граница, отделяющая знаковый разряд от значащих.
A 10 =+5 A 2 =+101 [A 2 ] П =[A 2 ] OK =0:101; B 10 =-13 B 2 =-1101 [B 2 ] OK =1:0010.
Свое название обратный код чисел получил потому, что коды цифр отрицательного числа заменены на инверсные. Укажем наиболее важные свойства обратного кода чисел:
• сложение положительного числа С с его отрицательным значением в обратном коде дает так называемую машинную единицу МЕок= 1: 111. 11, состоящую из единиц в знаковом и значащих разрядах числа;
A 10 =+19 A 2 =+10011 [A 2 ] П =[A 2 ] OK =[A 2 ] ДК =0:10011; B 10 =-13 В 2 =-1101 [B2] ДК =[B 2 ] OK +2 0 =1:0010+1=1:0011.
Укажем основные свойства дополнительного кода:
•сложение дополнительных кодов положительного числа С с его отрицательным значением дает так называемую машинную единицу дополнительного кода:
МЕ ДК =МЕ ОК +2 0 =10: 00…00,
т.е. число 10 (два) в знаковых разрядах числа;
•дополнительный код получил такое свое название потому, что представление отрицательных чисел является дополнением прямого кода чисел до машинной единицы МЕдк.
A 10 =9 A 2 =+1001 [A 2 ] П =[A 2 ] OK =[A 2 ] ДК =0:1001 [A 2 ] МОК =[A 2 ] МДК =00:1001;
B 10 =-9 B 2 =-1001 [B 2 ] OK =1:0110 [B 2 ] ДК =1:0111 [B 2 ] МОК =11:0110 [B 2 ] МДК =11:0111.
5.2. Арифметические операции над числами с фиксированной точкой
Сложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код. Пусть числа A=>O и В=>О, тогда операция алгебраического сложения выполняется в соответствии с табл. 2.3.
Таблица преобразования кодов при алгебраическом сложении
Скобки в представленных выражениях указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа. Сложение двоичных чисел осуществляется
последовательно, поразрядно в соответствии с табл. 2.2. При выполнении сложения цифр необходимо соблюдать следующие правила.
1. Выравнивание слагаемых. Слагаемые должны иметь одинаковое число разрядов. Для выравнивания разрядной сетки слагаемых можно дописывать незначащие нули слева к целой части числа и незначащие нули справа к дробной части числа.
2. Знаковые разряды чисел участвуют в сложении так же, как и значащие.
3. Необходимые преобразования кодов (п.5.1) производятся с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при
Пример 1. Сложить два числа А 10 =7 В 10 =16
Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки:
[A 2 ] П =[A 2 ] OK =[A 2 ] ДК =0: 00111;
[B 2 ] П =[B 2 ] OK =[B 2 ] ДК =0: 10000.
Сложение в обратном или дополнительном коде дает один и тот же результат
Обратим внимание, что при сложении цифр отсутствуют переносы в знаковый разряд и из знакового разряда, что свидетельствует о получении правильного результата.
При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда. В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда (см.п.4 правил). В случае ДК этот перенос игнорируется.
Умножение. Умножение двоичных чисел наиболее просто реализуется в прямом коде. Рассмотрим, каким образом оно приводится к операциям сложения и сдвигам.
Пример 3. Умножить два числа А 10 =7 В 10 =5.
Перемножим эти числа, представленные прямыми двоичными кодами, так же, как это делается в десятичной системе.
Нетрудно видеть, что произведение получается путём сложения частных произведений, представляющих собой разряды множимого, сдвинутые влево в соответствии с позициями разрядов множителя. Частные произведения, полученные умножением на нуль, игнорируются. Важной особенностью операции умножения n-разрядных сомножителей является увеличение разрядности произведения до n+n=2n. Знак произведения формируется путём сложения
знаковых разрядов сомножителей. Возможные переносы из знакового разряда игнорируются.
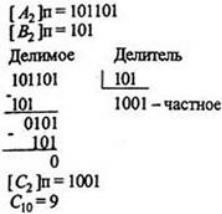
Деление. Операция деления, как и в десятичной арифметике, является обратной операции умножения. Покажем, что и эта операция приводится к последовательности операций сложения и сдвига.
Пример 4. Разделить два числа А 10 =45 B 10 =5
Знак частного формируется также путем сложения знаковых разрядов делимого и делителя, как это делалось при умножении.
5.3. Арифметические операции над двоичными числами
с плавающей точкой
В современных ЭВМ числа с плавающей точкой хранятся в памяти машин, имея мантиссу и порядок (характеристику) в прямом коде и нормализованном виде. Все арифметические действия над этими числами выполняются так же, как это делается с ними, если они представлены в полулогарифмической форме (мантисса и десятичный порядок) в десятичной системе счисления. Порядки и
мантиссы обрабатываются раздельно.
Сложение (вычитание). Операция сложения (вычитания) производится в следующей последовательности.
1. Сравниваются порядки (характеристики) исходных чисел путем их вычитания р=р1-р2. При выполнении этой операции определяется, одинаковый ли порядок имеют исходные слагаемые.
2. Если разность порядков равна нулю, то это значит, что одноименные разряды мантисс имеют одинаковые веса (двоичный порядок). В противном случае должно проводиться выравнивание порядков.
3. Для выравнивания порядков число с меньшим порядком сдвигается вправо на разницу порядков р. Младшие выталкиваемые разряды при этом теряются.
4. После выравнивания порядков мантиссы чисел можно складывать
(вычитать) в зависимости от требуемой операции. Операция вычитания заменяется операцией сложения в соответствии с данными табл. 2.3. Действия над слагаемыми производятся в ОК или ДК по общим правилам.
5. Порядок результата берется равным большему порядку p рез =max (p1,p2).
6. Если мантисса результата не нормализована, то осуществляются нормализация и коррекция значений порядка.
Пример. Сложить два числа А 10 =+ 1.375; B 10 =-0.625.
В нормализованном виде эти числа будут иметь вид:
Определяем, что р≠ 0.
2. Порядок первого числа больше порядка второго числа на единицу. Требуется выравнивание порядков.
3. Для выравнивания порядков необходимо второе число сдвинуть вправо на один разряд.
мантисса числа В в допол. коде [m’ B ]дк= 1: 1011 4. Складываем мантиссы.
5. Порядок числа С равен порядку числа с большим порядком, т.е. р c =
Видно, что мантисса результата не нормализована, так как старшая цифра мантиссы равна нулю.
6. Нормализуем результат путем сдвига мантиссы на один разряд влево
и соответственно вычитаем из значения порядка единицу:
Умножение (деление). Операция умножения (деления) чисел с плавающей точкой также требует разных действий над порядками и мантиссами. Алгоритмы этих операций выполняются в следующей последовательности.
1. При умножении (делении) порядки складываются (вычитаются) так, как это делается над числами с фиксированной точкой.
2. При умножении (делении) мантиссы перемножаются (делятся).
1. Сложение порядков (1+(-1)) 0:1 + 1:1
2. Перемножение мантисс 101*11=01111
3. Определение знака результата: 0+1=1 т.е. результат отрицательный
5.4. Арифметические операции над двоичнодесятичными кодами чисел
При обработке больших массивов экономической информации переводы чисел из десятичной системы в двоичную и обратно могут требовать значительного машинного времени. Некоторые образцы ЭВМ поэтому имеют или встроенные, или подключаемые блоки, которые обрабатывают десятичные целые числа в их двоично-десятичном представлении. Действия над ними также приводятся к операции алгебраического сложения отдельных цифр чисел, представленных дополнительными кодами в соответствии с табл. 2.3.
Приведем один из алгоритмов сложения, который получил довольно широкое распространение.
1. Сложение чисел начинается с младших цифр (тетрад) и производится с учетом возникающих переносов из младших разрядов в старшие.
2. Знак суммы формируется специальной логической схемой по знаку большего слагаемого.
5. Операция вычитания реализуется достаточно своеобразно. По общему правилу сложения (п.п.1-4) к тетрадам числа с большим модулем прибавляются дополнительные коды тетрад другого числа. В качестве знаке результата берется знак числа с большим модулем.
Правила арифметических операций в ЭВМ над машинными кодами.
Алгебраическое сложение. Параллельный сумматор. Учет переносов и переполнения. Определение знака результата. Особенности сложения и вычитания для прямых кодов. Двухпроводность операции вычитания прямых кодов. Формирование дополнений при вычитании. Реализация сложения и вычитания для дополнительных и обратных кодов.
Методы умножения. Умножение натуральных кодов. Методы реализации таблиц умножения. Машинная реализация умножения прямых кодов. Реализация методов умножения для дополнительных и обратных кодов. Влияние основания системы счисления на время реализации умножения.
Методы деления. Начальная установка делимого и делителя. Метод пробных вычитаний делителя из остатка. Машинная реализация методов для прямых, дополнительных и обратных кодов. Использование избыточного симметричного алфавита для оптимизации алгоритма деления без восстановления остатка. Особенности деления натуральных кодов с симметричным алфавитом.
Арифметические операции над числами с плавающей запятой. Сложение чисел с плавающей запятой. Выравнивание порядков. Сложение и округление мантисс. Нормализация результата. Правила сложения для очень больших и малых чисел и машинного нуля. Умножение и деление для чисел с плавающей запятой. Арифметические действия с числами при ненормализованной мантиссе.
Приближенные вычисления. Округление произведения и частного с учетом природы специфики операции умножения. Приближенное умножение с итеративным изменением длины множимого. Приближенное деление с итеративным изменением длины делителя. Оценки погрешности методов приближенного умножения и деления. Алгоритмы реализации арифметических операций с двойной и выше точностью.
Примеры я не нашла господа ищите сами.
Основой цифровой техники служат три логические операции, лежащие в основе всех выводов компьютера. Это три логические операции: И, ИЛИ, НЕ, которые называют «тремя китами машинной логики».
В компьютере логические функции реализуют логические элементы. Логический элемент (вентиль) – это часть электронной логической схемы, которая реализует элементарную логическую функцию, т.е. это электронная схема, которая формирует выходной сигнал в соответствии с простой булевой операцией преобразования сигналов, поданных на его входы.
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И–НЕ, ИЛИ–НЕ и другие, а также триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода.
Самой простой логической операцией является операция НЕ, по-другому ее часто называют отрицанием, дополнением или инверсией и обозначают NOT ( ).
Если А – истинно, то Ā – ложно и наоборот
Таблица истинности:
Результат отрицания всегда противоположен значению аргумента. Логическая операция НЕ является унарной, т.е. действие выполняются над одним операндом. В отличие от нее, операции И (AND) и ИЛИ (OR) являются бинарными, так как представляют собой результаты действий над двумя логическими величинами.
Например, A – идет дождь; Ā – не идет дождь (не(А) или not(A))
Логическое И еще часто называют конъюнкцией, или логическим умножением, а ИЛИ – дизъюнкцией, или логическим сложением.
Операция И (обозначается «И», «and», «&», А•В) имеет результат «истина» только в том случае, если оба ее операнда истинны.
Таблица истинности:
Если F = A&B, то F истинно тогда и только тогда,
Когда истинны и А и В
Например, A – пасмурно; B – идет дождь.
Можно записать: A&B (читается пасмурно и идет дождь)
Операция ИЛИ (обозначается «ИЛИ», «or», А+В) «менее привередлива» к исходным данным. Она дает «истину», если значение «истина» имеет хотя бы один из операндов. Разумеется, в случае, когда справедливы оба аргумента одновременно, результат по-прежнему истинный.
Таблица истинности:
Если F = A+B, то F ложно тогда и только тогда, когда ложны и А и В.
Например, A – пасмурно; B – идет дождь.
Можно записать: A+B (читается пасмурно или идет дождь)
Операции И, ИЛИ, НЕ образуют полную систему логических операций, из которой можно построить сколь угодно сложное логическое выражение. В вычислительной технике также часто используется операции импликация и эквивалентность.
Таблица истинности:
Логическая равнозначность: эквивалентность – определяет результат сравнения двух простых логических выражений А и В. Результатом эквивалентности является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначается символом «эквивалентности».
Таблица истинности:
Вопрос 10
В вычислительных машинах коды нуля и единицы представляются электрическими сигналами, имеющими два различных состояния. Наиболее распространенными способами физического представления информации являются импульсный и потенциальный:
· импульс или его отсутствие;
· высокий или низкий потенциал;
· высокий потенциал или его отсутствие.
При импульсном способе отображения код единицы идентифицируется наличием электрического импульса, код нуля — его отсутствием (впрочем, может быть и наоборот). Импульс характеризуется амплитудой и длительностью, причем длительность должна быть меньше временного такта машины.
При потенциальном способе отображения код единицы — это высокий уровень напряжения, а код нуля — отсутствие сигнала или низкий его уровень. Уровень напряжения не меняется в течение всего такта работы машины. Форма и амплитуда сигнала при этом во внимание не принимаются, а фиксируется лишь сам факт наличия или отсутствия потенциала.
Вышесказанное обусловило то, что для анализа и синтеза схем в компьютере при алгоритмизации и программировании решения задач широко используется математический аппарат алгебры логики, оперирующий также с двумя понятиями «истина» или «ложь».
Элементы алгебры логики
Алгебра логики— это раздел математической логики, значение всех элементов (функций и аргументов) которой определены в двухэлементном множестве: 0 и 1. Алгебра логики оперирует с логическими высказываниями.
Высказывание — это любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности. При этом считается, что высказывание удовлетворяет закону исключенного третьего, то есть каждое высказывание или истинно, или ложно, и не может быть одновременно и истинным и ложным.
· «Сейчас идет снег» — это утверждение может быть истинным или ложным;
· «Вашингтон — столица США» — истинное утверждение;
· «Частное от деления 10 на 2 равно 3» — ложное утверждение.
В алгебре логики все высказывания обозначают буквами а, b, с и т. д. Содержание высказываний учитывается только при введении их буквенных обозначений, и в дальнейшем над ними можно производить любые действия, предусмотренные данной алгеброй. Причем если над исходными элементами алгебры выполнены некоторые разрешенные в алгебре логики операции, то результаты операций также будут элементами этой алгебры.
Простейшими операциями в алгебре логики являются операции логического сложения(иначе: операция ИЛИ (OR), операция дизъюнкции) и логического умножения(иначе: операция И (AND), операция конъюнкции). Для обозначения операции логического сложения используют символы + или V, а логического умножения — символы • или /\. Правила выполнения операций в алгебре логики определяются рядом аксиом, теорем и следствий. В частности, для алгебры логики применимы следующие законы.
а ∙ (b + с) = а ∙ b + a ∙ с,
(а + b) ∙ с = а ∙ с + b ∙ с.
Справедливы соотношения, в частности:
а + а = а, а + b = b, если а ≤ b,
а ∙ а = а, a ∙ b = а, если а ≤ b,
а + a ∙ b = a, a ∙ b = b, если а ≥ b,
Наименьшим элементом алгебры логики является 0, наибольшим элементом — 1. В алгебре логики также вводится еще одна операция — отрицания(операция НЕ, инверсия), обозначаемая чертой над элементом.

Справедливы, например, такие соотношения:
Функция в алгебре логики — выражение, содержащее элементы алгебры логики а, b, с и др., связанные операциями, определенными в этой алгебре.
Примеры логических функций:
Для любой операции, определенной в алгебре логики существуют таблицы истинности – таблицы, в которых приведены значения операции в зависимости от значений высказываний над которыми выполняется данная операция.
Функция конъюнкции истинна тогда, когда истинны одновременно оба высказывания.
Дизъюнкция
Это сложное высказывание истинно тогда, когда истинно хотя бы одно высказывание, входящее в него.
Читается X1 ИЛИ X2: часто это высказывание называют логическим сложением.
Логическая равнозначность
Это сложное высказывание истинно тогда, когда истинны или ложны одновременно оба высказывания.
Отсюда следует, что вне зависимости от смысла, равнозначными являются как истинные, так и ложные высказывания.
Импликация
Это сложное высказывание ложно только тогда, когда X1 – истинно, а X2 – ложно.
Читается: если X1, то X2. При этом X1 – посылка, X2 – следствие.
Эквивалентности
В некоторых случаях сложное и длинное высказывание можно записать более коротким и простым без нарушения истинности исходного высказывания. Это можно выполнить с использованием некоторых эквивалентных соотношений.
т.е. истинность высказывания не изменится, если его заменить более коротким, таким образом, это правило приведения подобных членов:

– постоянно истинное высказывание.
0 
x1 

— (переместительный) коммуникативный закон.
x1 





х 





правило приведения подобных членов:
1 
Сложение по mod 2
1 


Правило де Моргана
Докажем для двух переменных с помощью таблицы истинности:
| Х1 | Х2 | Х1  Х2 Х2 | X1 & X2 |
Х 

Операция полного склеивания:
XY 

Операция неполного склеивания:
XY