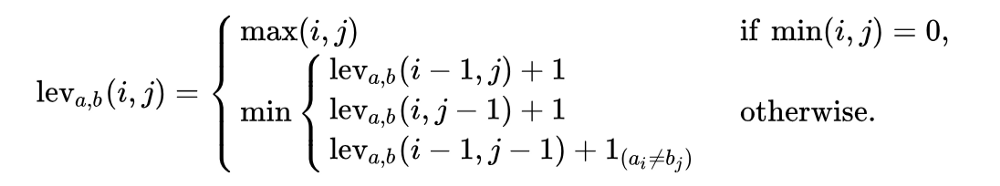Алгоритм «Разделяй и властвуй»
В этой статье вы узнаете, как работает алгоритм «разделяй и властвуй», а также чем он отличается от других способов решения рекурсивных задач.
Алгоритм «разделяй и властвуй» помогает решать большие задачи. Вот как это происходит:
Чтобы использовать алгоритм «разделяй и властвуй», понадобятся знания о рекурсии.
Как работает алгоритм
Алгоритм стоит из 3 шагов:
Разберем этот алгоритм на примере.
Мы будем выполнять сортировку слиянием с помощью алгоритма «разделяй и властвуй».
1. Пусть дан следующий массив:
2. Делим его пополам:
Рекурсивно делим подмассивы до тех пор, пока не останутся только отдельные элементы.
3. Объединяем и сортируем отдельные элементы. На этом этапе мы властвуем и объединяем:
Временная сложность
Сложность алгоритма «разделяй и властвуй» вычисляется с помощью основной теоремы о рекуррентных соотношениях:
Попробуем найти временную сложность рекурсивной задачи.
В качестве примера возьмем сортировку слиянием. Уравнение принимает следующий вид:
«Разделяй и властвуй» vs. динамическое программирование
Суть метода «разделяй и властвуй» заключается в том, что мы делим задачу на меньшие подзадачи. После этого подзадачи рекурсивно вычисляются. Результаты вычисления каждой подзадачи при использовании этого метода не сохраняются. А в динамическом программировании — наоборот. Результаты вычисления каждой подзадачи сохраняются для будущего использования.
Используйте метод «разделяй и властвуй», когда все подзадачи дают разный результат. Динамическое программирование лучше использовать, когда результаты вычислений подзадач могут совпадать.
Разберем пример. Допустим, мы пытаемся найти числа Фибоначчи.
«Разделяй и властвуй»
Динамическое программирование
Разделяй и властвуй (программирование)
Разделяй и властвуй (англ. divide and conquer ) — в информатике важная парадигма разработки алгоритмов. Основана на рекурсивном разбиении решаемой задачи на две (или более) подзадачи того же типа, но меньшего размера. Разбиения выполняются до тех пор, пока все подзадачи не окажутся элементарными.
Литература
Ссылки
Смотреть что такое «Разделяй и властвуй (программирование)» в других словарях:
Разделяй и Властвуй — Разделяй и властвуй: Разделяй и властвуй (политика) политический принцип. Разделяй и властвуй (программирование) парадигма разработки алгоритмов. Разделяй и Властвуй (игра) компьютерная игра. Разделяй и властвуй / Divide And Conquer эпизод… … Википедия
Разделяй и властвуй! — Разделяй и властвуй: Разделяй и властвуй (политика) политический принцип. Разделяй и властвуй (программирование) парадигма разработки алгоритмов. Разделяй и Властвуй (игра) компьютерная игра. Разделяй и властвуй / Divide And Conquer эпизод… … Википедия
Разделяй и властвуй (информатика) — У этого термина существуют и другие значения, см. Разделяй и властвуй (значения). Разделяй и властвуй (англ. divide and conquer) в информатике важная парадигма разработки алгоритмов, заключающаяся в рекурсивном разбиении решаемой задачи … Википедия
РиВ — Разделяй и властвуй: Разделяй и властвуй (политика) политический принцип. Разделяй и властвуй (программирование) парадигма разработки алгоритмов. Разделяй и Властвуй (игра) компьютерная игра. Разделяй и властвуй / Divide And Conquer эпизод… … Википедия
Список алгоритмов — Эта страница информационный список. Основная статья: Алгоритм Ниже приводится список алгоритмов, группированный по категориям. Более детальные сведения приводятся в списке структур данных и … Википедия
Программируемые алгоритмы — Служебный список статей, созданный для координации работ по развитию темы. Данное предупреждение не устанавл … Википедия
Управление — Эта статья предлагается к удалению. Пояснение причин и соответствующее обсуждение вы можете найти на странице Википедия:К удалению/30 августа 2012. Пока процесс обсуждения не завершён, статью можн … Википедия
Детектор затарков — (англ. Zatarc detector) вымышленное устройство в телесериале Звёздные врата SG 1, которое является очень эффективным детектором лжи. Ток ра используют детектор для проверки жертв манипуляции сознанием гоа’улдами затарков (спящих агентов,… … Википедия
Троичный поиск — (Тернарный поиск) это метод в информатике для поиска максимумов и минимумов функции, которая либо сначала строго возрастает, затем строго убывает, либо наоборот. Троичный поиск определяет, что минимум или максимум не может лежать либо в первой,… … Википедия
Технологии Ток\’ра в Звёздных вратах — Ток ра используют в основном технологии гоаулд. Это связан как с их физиологией, так и с характером их действий. Однако для выполнения спцифических задач они разрабатывают свои устройства и заимствуют технологии других например толланское… … Википедия
Динамическое программирование или «Разделяй и Властвуй»
В этой статье рассматриваются сходства и различия двух подходов к решению алгоритмических задач: динамического программирования (dynamic programing) и принципа «разделяй и властвуй» (divide and conquer). Сравнение будем производить на примере, соответственно, двух алгоритмов: бинарного поиска (как быстро найти число в отсортированном массиве) и расстояния Левенштейна (как преобразовать одну строку в другую с минимальным количеством операций).
Хочу сразу заметить, что данное сравнение и объяснение не претендует на исключительную правильность. И возможно даже некоторые преподаватели в университетах захотели бы меня отчислить 

Проблема
Когда я начал изучать алгоритмы мне было сложно понять основную идею динамического программирования (далее DP, от Dynamic Programming) и чем оно отличается от подхода «разделяй и властвуй» (далее DC, от divide-and-conquer). Когда дело доходит до сравнения этих двух парадигм обычно многие успешно используют функцию Фибоначчи для иллюстрации. И это отличная иллюстрация. Но мне кажется, что когда мы используем одну и ту же задачу для иллюстрации DP и DC, то мы теряем одну важную деталь, которая может помочь нам уловить различие между двумя подходами быстрее. И эта деталь состоит в том, что эти две техники наилучшим образом проявляются при решении разного типа задач.
Я все еще в процессе изучения DP и DC и не могу сказать, что я полностью разобрался с этими концепциями. Но я все же надеюсь, что эта статья прольет дополнительный свет и поможет сделать очередной шаг в изучении таких значимых подходов, как dynamic programming and divide-and-conquer.
Сходство DP и DC
То, как я вижу эти две концепции сейчас, могу заключить, что DP является расширенной версией DC.
Я бы не считал их чем-то совершенно различным. Потому что обе эти концепции рекурсивно разбивают проблему на две или более подпроблемы одного и того-де типа до тех пор, пока эти подпроблемы не станут достаточно легкими, чтобы решить их «в лоб», непосредственно. Далее все решения подпроблем объединяются вместе для того, чтобы в итоге дать ответ на оригинальную, изначальную проблему.
Итак, почему же тогда мы все еще имеем два разных подхода (DP и DC) и почему я назвал динамическое программирование расширением. Это потому, что динамическое программирование может быть применено к задачами, которые обладают определенными характеристиками и ограничениями. И только в этом случае DP расширяет DC посредством двух техник: мемоизации (memoization) и табуляции (tabulation).
Давайте немного углубимся в детали…
Ограничения и характеристики необходимые для динамического программирования
Как мы только что с вами выяснили, есть две ключевых характеристики, которыми должна обладать задача/проблема для того, чтобы мы могли попытаться решить ее с помощью динамического программирования:
Динамическое программирование, как расширение принципа «разделяй и властвуй»
Мемоизация (заполнения кеша сверху-вниз) является техникой кеширования, которая использует заново ранее вычисленные решения подзадач. Функция Фибоначчи с использованием техники мемоизации выглядела бы так:
Табуляция (заполнение кеша снизу-вверх) является схожей техникой, но которая в первую очередь сфокусирована на заполнении кеша, а не на поиске решения подпроблемы. Вычисление значений, которые необходимо поместить в кеш легче всего в данном случае выполнять итеративно, а не рекурсивно. Функция Фибоначчи с использованием техники табуляции выглядела бы так:
Более детально о сравнении мемоизации и табуляции вы можете прочитать здесь.
Основная мысль, которую необходимо уловить в этих примерах, заключается в том, что поскольку у нашей DC проблемы есть пересекающиеся подпроблемы, то мы можем использовать кеширование решений подпроблем с помощью одной из двух техник кеширования: мемоизации и табуляции.
Итак, в чем же в конце концов разница между DP и DC
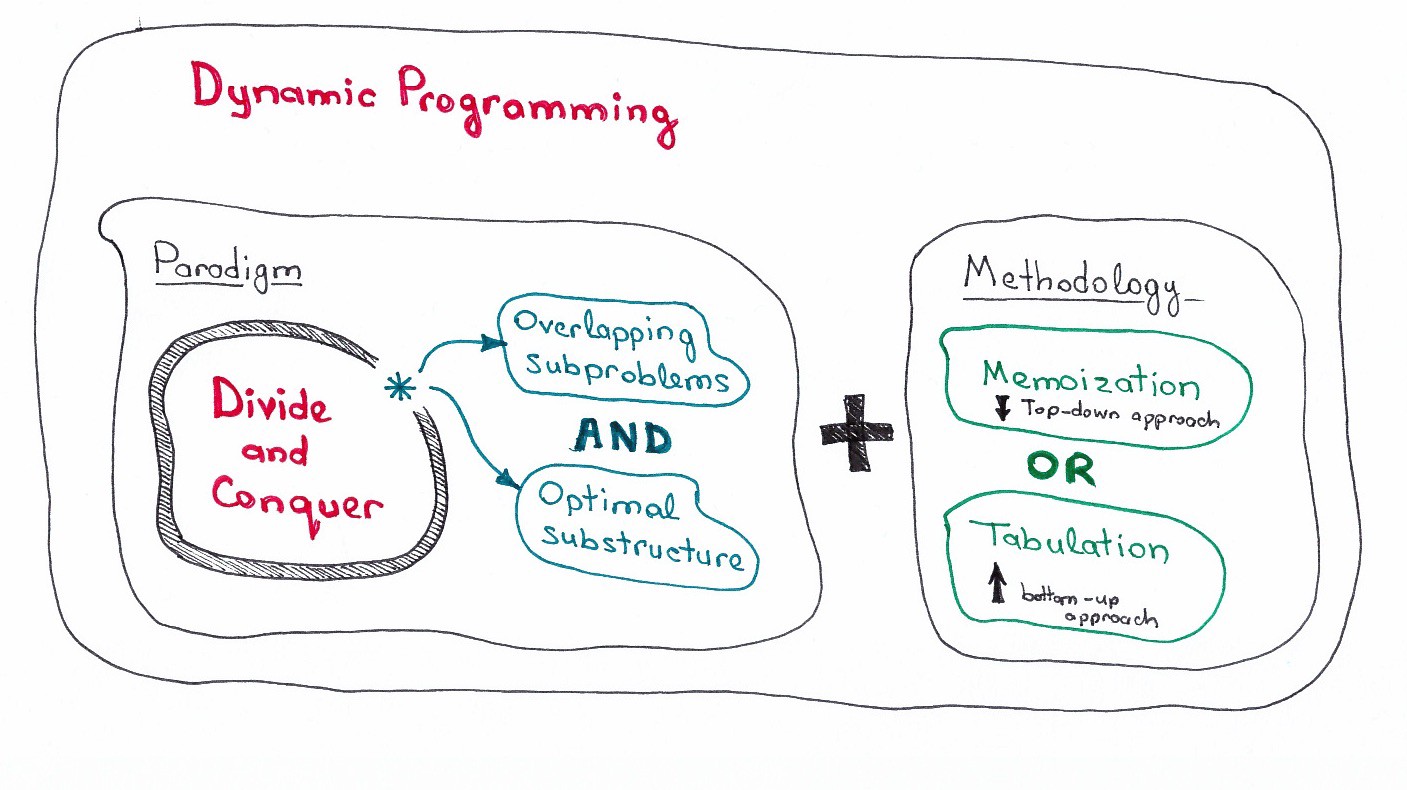
Мы ознакомились с ограничениями и предпосылками использования динамического программирования, а так же с техниками кеширования используемыми в DP подходе. Давайте попытаемся суммировать и изобразить изложенные выше мысли в следующей иллюстрации:
Давайте попытаемся решить пару задач с использованием DP и DC, чтобы продемонстрировать оба этих подхода в действии.
Пример принципа «разделяй и властвуй»: Бинарный поиск
Алгоритм бинарного поиска является поисковым алгоритмом, который находит позицию запрашиваемого элемента в отсортированном массиве. В бинарном поиске мы сравниваем значение искомой переменной со значением элемента в середине массива. Если они не равны, то половина массива, в которой искомый элемент не может находиться исключается из дальнейшего поиска. Поиск продолжается в той половине массива, в которой может находиться искомая переменная до тех пор, пока она не будет найдена. Если же очередная половина массива не содержит элементов, поиск считается законченными и мы делаем вывод, что массив не содержит искомого значения.
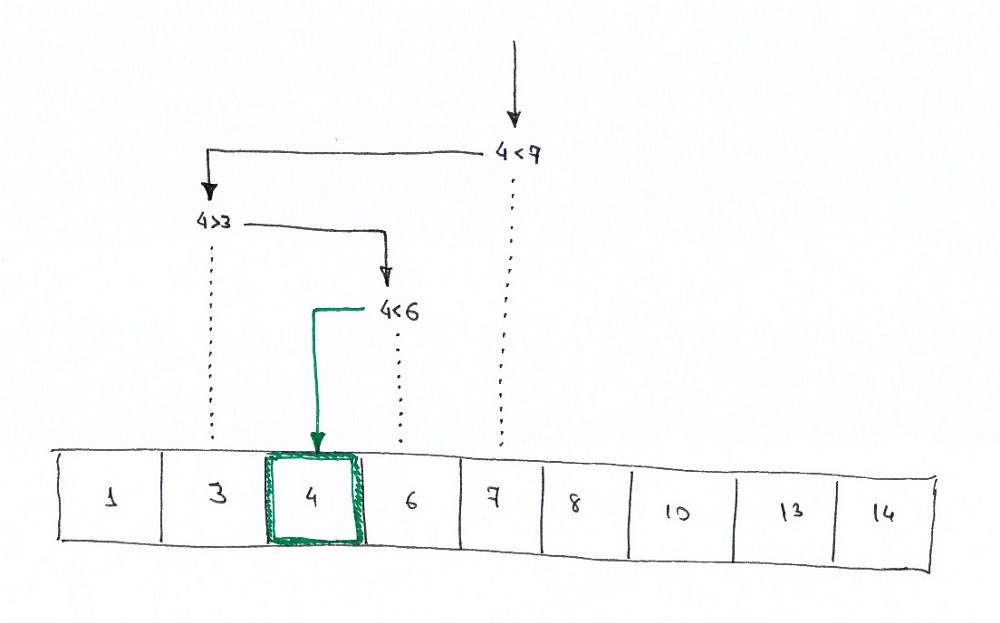
На иллюстрации ниже — пример бинарного поиска числа 4 в массиве.
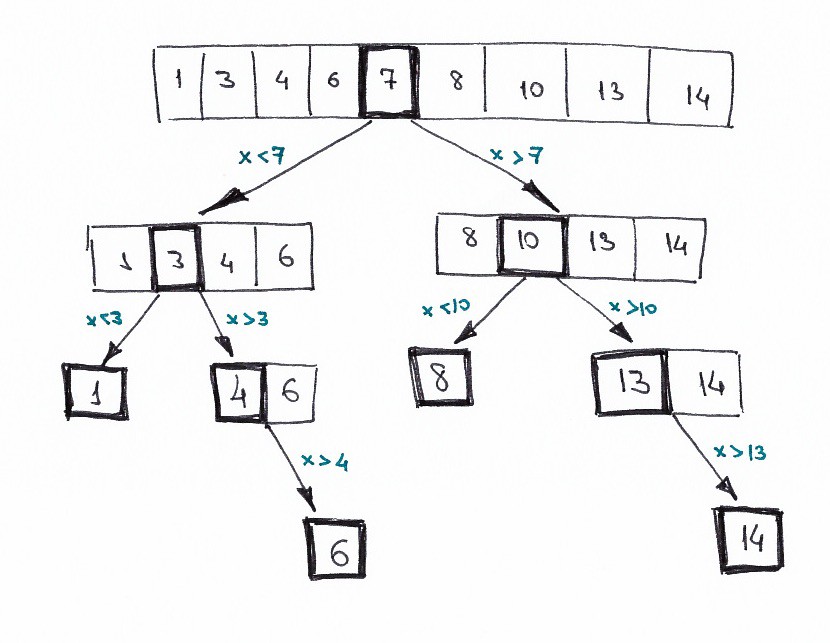
Давайте изобразим ту же логику поиска но в форме «дерева решений» (decision tree).
Вы можете увидеть в этой схеме четкий принцип «разделяй и властвуй», используемый для решения этой проблемы. Мы итеративно разбиваем наш оригинальный массив на подмассивы и пытаемся найти искомый элемент уже в них.
Можем ли мы решить эту задачи с использованием динамического программирования? Нет. По той причине, что данная задача не содержит пересекающихся подпроблем. Каждый раз, когда мы разбиваем массив на части, обе части являются полностью независимыми и не пересекающимися. А согласно предпосылкам и ограничениям динамического программирования, которые мы обсуждали выше, подпроблемы должны каким-то образом пересекаться, они должны быть повторяющимися.
Обычно, всякий раз, когда дерево решений выглядит именно как дерево (а не как граф), это скорее всего означает отсутствие пересекающихся подпроблем,
Здесь вы можете найти полный исходный код алгоритма бинарного поиска с тестами и объяснениями.
Пример динамического программирования: Дистанция редактирования
Обычно, когда дело доходит до объяснения динамического программирования, в качестве примера используется функция Фибоначчи. Но в нашем случае, давайте возьмем немного более сложный пример. Чем больше примеров, тем легче разобраться с концепцией.
Дистанция редактирования (или расстояние Левенштейна) между двумя строками это минимальное количество операций вставки одного символа, удаления одного символа и замены одного символа на другой, необходимых для превращения одной строки в другую.
Например, дистанция редактирования между словами «kitten» and «sitting» равна 3, поскольку необходимо произвести три операции редактирования (две замены и одну вставку), чтобы преобразовать одну строку в другую. И невозможно найти более быстрый вариант преобразования с меньшим количеством операций:
Алгоритм имеет широкую область применения, например, для проверки орфографии, систем корректировки оптического распознавания, неточный поиск строки и пр.
Математическое определение проблемы
Обратите внимание, первая строка в функции min соответствует операции удаления, вторая строка соответствует операции вставки и третья строка соответствует операции замены (в случае, если буквы не равны).
Давайте попробуем разобраться, о чем нам говорит эта формула. Возьмем простой пример поиска минимальной дистанции редактирования между строками ME и MY. Интуитивно вы уже знаете, что минимальная дистанция редактирования равна одной (1) операции замены (заменить «E» на «Y»). Но давайте формализуем наше решение и превратим его в алгоритмическую форму, для того, чтобы иметь возможность решать более сложные версии этой задачи, такой как трансформация слова Saturday в Sunday.
Для того, чтобы применить формулу к трансформации ME→MY мы сначала должны узнать минимальную дистанцию редактирования между ME→M, M→MY и M→M. Далее мы должны выбрать из трех дистанций минимальную и добавить к ней одну операцию (+1) трансформации E→Y.
Итак, мы уже можем увидеть рекурсивную природу этого решения: минимальная дистанция редактирования ME→MY вычисляется на основании трех предыдущих возможных трансформаций. Таким образом мы уже можем сказать, что это алгоритм «разделяй и властвуй».
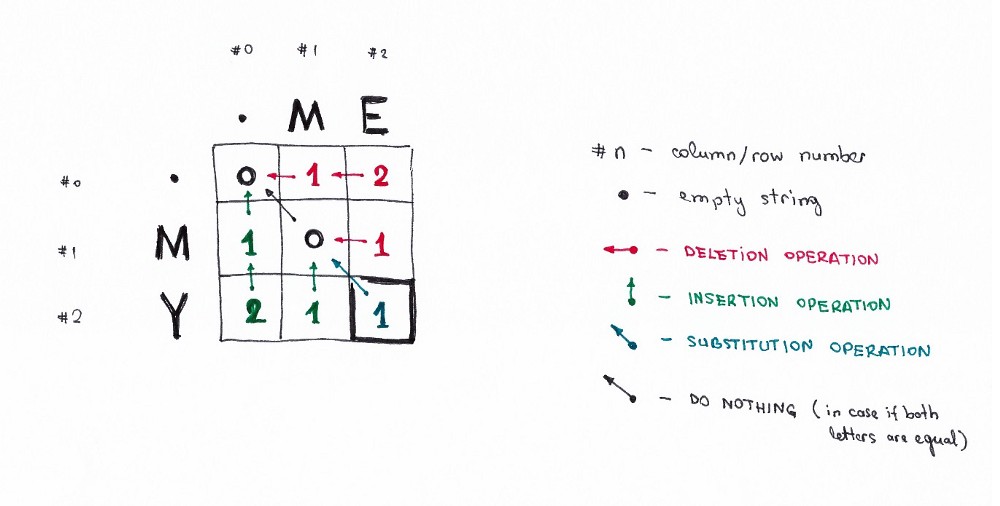
Для дальнейшего объяснения алгоритма давайте поместим две наших строки в матрицу:
Ячейка (0,1) содержит красное число 1. Это означает, то нам необходимо выполнить 1 операцию для того, чтобы преобразовать M в пустую строку — удалить M. Поэтому мы обозначили это число красным цветом.
Ячейка (0,2) содержит красное число 2. Это означает, что нам надо выполнить 2 операции для того, чтобы трансформировать строку ME в пустую строку — удалить E, удалить M.
Ячейка (1,0) содержит зеленое число 1. Это означает, что нам необходима 1 операция, чтобы трансформировать пустую строку в M — вставить M. Операцию вставки мы отметили зеленым цветом.
Ячейка (2,0) содержит зеленое число 2. Это означает, что нам необходимо выполнить 2 операции для того, чтобы преобразовать пустую строку в строку MY — вставить Y, вставить M.
Ячейка (1,1) содержит число 0. Это означает, что нам не надо делать ни одно операции, для того, чтобы преобразовать строку M в M.
Ячейка (1,2) содержит красное число 1. Это означает, что нам необходимо выполнить 1 операцию, чтобы трансформировать строку ME в М — удалить E.
Это выглядит не сложно для маленьких матриц, таких как наша (всего 3х3). Но как мы можем рассчитать значения всех ячеек для больших матриц (как например для матрицы 9х7 при трансформации Saturday→Sunday)?
Итак, повторюсь, вы можете четко увидеть рекурсивную природу данной задачи.
Мы так же увидели, что имеем дело с задачей типа «разделяй и властвуй». Но, можем ли мы применить динамическое программирование для решения этой задачи? Удовлетворяет ли данная задача упомянутым выше условиям «пересекающихся проблем» и «оптимальных подструктур«? Да. Давайте построим дерево принятий решений.
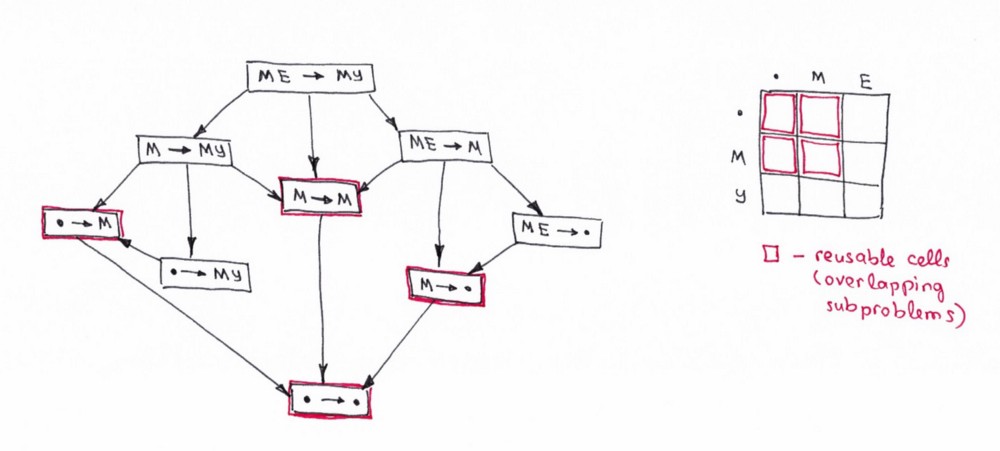
Во-первых вы можете заметить, что наше дерево решений выглядит скорее не как дерево, а как граф решений. Вы так же можете заметить несколько пересекающихся подзадач. Так же видно, что невозможно уменьшить количество операций и сделать его меньшим, чем количество операций с тех трех соседних ячейках (подпроблемах).
Так же вы можете заметить, что значение в каждой ячейке вычисляется на основании предыдущих значений. Таким образом в данном случае применяется техника табуляции (заполнение кеша в направлении снизу-вверх). Вы увидите это в примере кода ниже.
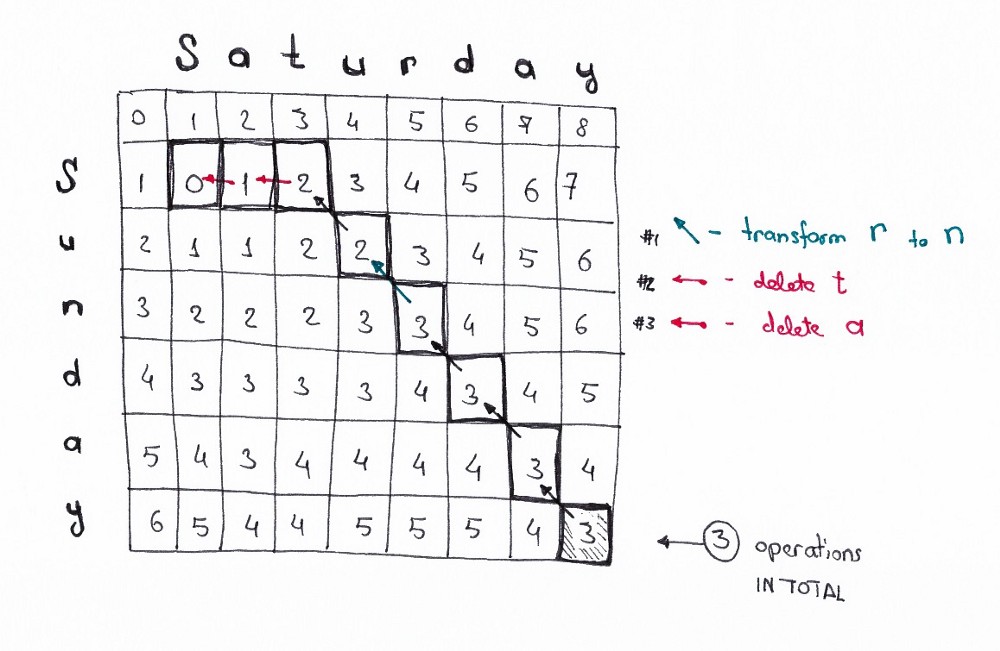
Применяя все эти принципы, мы можем решать более сложные задачи, например задачу трансформации Saturday→Sunday:
Здесь вы можете найти полное решение поиска минимальной дистанции редактирования с тестами и объяснениями:
Выводы
В этой статье мы сравнили два алгоритмических подхода («динамическое программирование» и «разделяй и властвуй») к решению задач. Мы обнаружили, что динамическое программирование использует принцип «разделяй и властвуй» и можем быть применимо к решению задач в случае, если задача содержит пересекающиеся подпроблемы и оптимальную подструктуру (как в случае с расстоянием Левенштейна). Динамическое программирование далее использует техники мемоизации и табуляции для сохранения подрешений для дальнейшего их повторного использования.
Я надеюсь эта статья скорее прояснила, а не усложнила ситуацию для тех из вас, кто пытался разобраться с такими важными концепциями как динамическое программирование и «разделяй и властвуй» 
Вы можете найти больше алгоритмических примеров, использующих динамическое программирование, с тестами и объяснениями в репозитории JavaScript Algorithms and Data Structures.
Динамическое программирование VS «Разделяй и властвуй»
Динамическое программирование или подход «разделяй и властвуй»? В этой статье рассматриваем сходства и различия двух способов.
В качестве примеров будут рассмотрены алгоритмы бинарного поиска и вычисления минимальной дистанции редактирования (расстояние Левенштейна).
В чём вопрос
При изучении алгоритмов многие сталкиваются с трудностями в понимании идеи динамического программирования и отличий динамического подхода (dynamic programming, DP) от подхода «разделяй и властвуй» (divide-and-conquer, DC). Обычно при сравнении этих двух парадигм приводятся в пример соответствующие тому и другому подходу алгоритмы вычисления чисел Фибоначчи. Но пытаясь продемонстрировать обе парадигмы на одном и том же примере, мы можем упустить из виду важную деталь. Она заключается в том, что DP и DC нужны для разных типов задач.
Сходство DP и DC
Обе парадигмы похожи тем, что работают путем рекурсивного разбиения задачи на две или более подзадач того же или похожего типа. Разбиение продолжается, пока подзадачи не станут настолько простыми, чтобы их можно было решить напрямую, а затем их решения объединяются для получения ответа.
Динамическое программирование позволяет оптимизировать задачу «разделяй и властвуй». В то же время важно заметить, что подход динамического программирования не универсален: он может быть использован только в том случае, если задача удовлетворяет определенным ограничениям.
Ограничения на задачу для DP
Существует два ключевых ограничения, которые должны выполняться у задачи «разделяй и властвуй», чтобы для ее решения можно было использовать динамическое программирование:
Если эти два условия выполнены, задача может быть оптимизирована с использованием динамического программирования.
Как работает динамическое программирование
Динамическое программирование дополняет «разделяй и властвуй» с помощью техник, известных как мемоизация и табуляция. Смысл обеих заключаются в кэшировании решений перекрывающихся подзадач для того, чтобы повторно их использовать, не пересчитывая заново. Такой подход может существенно повысить производительность за счет использования большего количества памяти на кэш. Например, простая рекурсивная реализация функции Фибоначчи (функции, вычисляющей n-ное число Фибоначчи) имеет экспоненциальную временную сложность, а решение динамическим программированием справляется с задачей за линейное время.
Мемоизация (memoization, заполнение кэша сверху вниз) заключается в кэшировании и повторном использовании ранее вычисленных результатов. Так, memoized fib будет выглядеть следующим образом:
Табуляция (tabulation, заполнение кэша снизу-вверх) похожа на мемоизацию, но фокусируется на заполнении кэша. Вычисление значений в кэше выполняется итеративно. Так будет выглядеть соответствующая версия функции fib:
Больше о мемоизации и табуляции, а также их сравнительном анализе можно почитать здесь.
Основная идея, которую нужно усвоить, состоит в следующем: если задача «разделяй и властвуй» имеет перекрывающиеся подзадачи, становится возможной оптимизация программы путем кэширования вычисленных решений подзадач с помощью мемоизации или табуляции.
В чем же разница между DC и DP?
Поскольку мы уже разобрались, в чем состоят требования динамического программирования к задаче, и какие существуют методологии кэширования, попробуем объединить изученное в одну общую картину.
Давайте решим пару задач, используя обе парадигмы, чтобы немного прояснить иллюстрацию.
Пример DC-задачи: бинарный поиск
Алгоритм бинарного поиска представляет собой алгоритм, который находит индекс целевого значения в отсортированном массиве. Бинарный поиск сравнивает целевое значение с центральным элементом массива. Если они не равны, то искомый элемент может содержаться только в одной из половин массива. Такой вывод мы можем сделать из предположения о том, что массив отсортирован.
Если искомый элемент больше центрального, то мы продолжаем поиск в большей половине массива, а если меньше – то, соответственно, в меньшей. И так до тех пор, пока нецелевое значение не будет найдено. А если поиск заканчивается тем, что оставшаяся половина пуста, можно утверждать, что массив не содержит искомого элемента.
Пример
Ниже представлена визуализация работы алгоритма бинарного поиска, где целевым значением является 4.
Нарисуем то же самое, но в виде дерева решений.
В логике бинарного поиска ясно прослеживается принцип «разделяй и властвуй». Мы итеративно делим исходный массив, каждый раз уменьшая область поиска и сводя задачу к тривиальной.
Можем ли мы задействовать динамическое программирование? Нет. Подзадачи, возникающие при дроблении массива, совершенно независимы. Они не перекрываются, а это одно из ограничений, которым должна соответствовать задача DP.
Если решая некоторую задачу, вы нарисуете дерево решений, и это действительно дерево, а не граф, значит, перекрывающихся задач нет, и динамическое программирование применить нельзя.
Немного кода
Здесь можно найти исходный код бинарного поиска с пояснениями и тестами.
Пример DP-задачи: дистанция редактирования
Классической иллюстрацией задачи динамического программирования служит алгоритм нахождения числа Фибоначчи. Но мы возьмем немного более сложный алгоритм ради разнообразия. Это поможет лучше понять концепцию.
Минимальное расстояние редактирования (или расстояние Левенштейна) − это метрика для измерения разницы между двумя последовательностями символов.
Неформально расстояние Левенштейна между двумя словами определяется как минимальное количество односимвольных изменений (вставка, удаление или замена символа), необходимое для трансформации одного слова в другое.
Пример
Расстояние Левенштейна между словами «kitten» и «sitting» равно 3. Приведенная ниже последовательность односимвольных изменений меняет одно слово на другое, и, на самом деле, нет никакого способа сделать это за меньшее количество действий.
Приложения
Эта метрика имеет широкий спектр приложений: проверка орфографии, системы коррекции для оптического распознавания символов, поиск нечетких строк и программное обеспечение для перевода естественного языка.
Математическое определение
Математически расстояние Левенштейна между двумя строками a и b (длины |a| и |b| соответственно) задается функцией lev(|a|, |b|), определяемой следующим образом:
Обратите внимание, что первое выражение в min соответствует удалению (от a до b), второе − вставке, а третье − совпадению или несоответствию, в зависимости от того, являются ли соответствующие символы одинаковыми. Далее мы немного подробнее это разберем.
Пояснение
Давайте попробуем разобраться, о чем говорит данная формула. Рассмотрим простой пример: требуется найти минимальное расстояние редактирования между строками ME и MY. Интуитивно понятно, что минимальное расстояние редактирования здесь − 1 операция, и эта операция − «заменить E на Y». Но давайте попробуем формализовать интуитивные рассуждения и привести их к алгоритму, чтобы иметь возможность решать более сложные примеры, например, преобразование «Saturday» в «Sunday».
Чтобы применить формулу к преобразованию ME → MY, нам нужно знать минимальные расстояния редактирования преобразований ME → M, M → MY и M → M в предыдущем. Затем нам нужно будет выбрать минимальный и добавить +1 операцию для преобразования последних букв E → Y.
Заметен рекурсивный характер решения: минимальное расстояние редактирования трансформация вычисляется на основе трех ранее возможных преобразований. Это наталкивает на мысль о том, что алгоритм решения этой задачи следует принципу «разделяй и властвуй».
Давайте нарисуем следующую матрицу:
Что содержится в ячейках
(1,1): содержит число 0. Это означает, для преобразования M в M не требуется никаких операций.
Выглядит просто для такой маленькой матрицы. Но как вычислять все эти числа для больших матриц (скажем, 9×7, для Saturday → Sunday)?
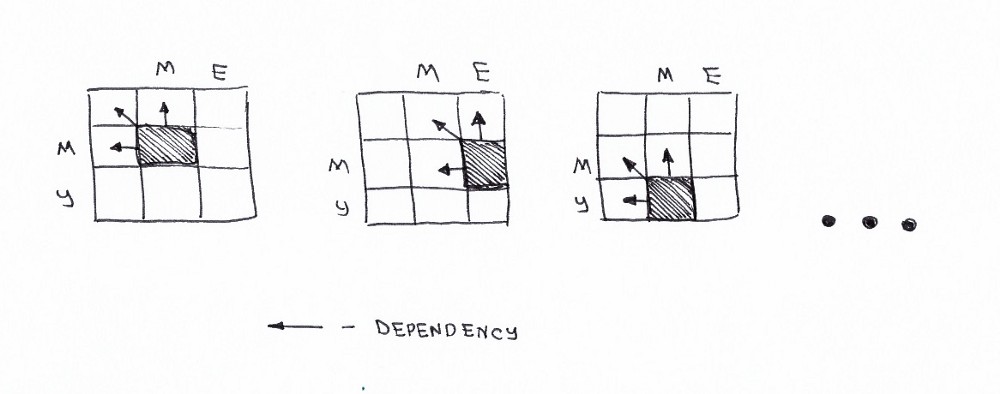
Хорошая новость: согласно формуле, вам нужны только три соседние ячейки (i-1, j), (i-1, j-1) и (i, j-1) для вычисления числа для текущей ячейки (i, j). Все, что нам нужно сделать, − это найти минимум трех ячеек, а затем добавить +1 в случае, если у нас есть разные символы в строке i и столбце j.
Рекурсивный характер проблемы очевиден.
Здорово! Мы только что выяснили, что имеем дело с задачей «разделяй и властвуй». Но можем ли мы применить к ней подход динамического программирования? Удовлетворяет ли эта задача ограничениям, заключающимся в наличии перекрывающихся подзадач и оптимальной подструктуры? Да. Посмотрим на граф решений.
Прежде всего еще раз отметим, что это не дерево решений. Это граф. Заметны несколько перекрывающихся подзадач на изображении, отмеченных красным. Также нет способа уменьшить количество операций.
Отметим, что каждый номер ячейки в матрице вычисляется на основе предыдущих. Таким образом, здесь применяется методика табуляции (заполнение кеша снизу вверх). Вы увидите это в примере кода ниже.
Применяя эти принципы, мы можем решить более сложные случаи. Например, дистанция редактирования Saturday → Sunday.
Исходный код
Заключение
В этой статье мы сравнили два алгоритмических подхода: динамическое программирование и «разделяй и властвуй». Мы выяснили, что динамическое программирование основано на «разделяй и властвуй» и может применяться только в том случае, если проблема имеет перекрывающиеся подзадачи и оптимальную подструктуру (метрика Левенштейна послужила прекрасной тому иллюстрацией). Алгоритм решения задачи динамического программирования использует мемоизацию или табуляцию для хранения решений перекрывающихся подзадач для последующего использования.
Больше примеров задач «разделяй и властвуй» и динамического программирования с пояснениями, комментариями и примерами тестов можно найти в репозитории JavaScript Algorithms и Data Structures.