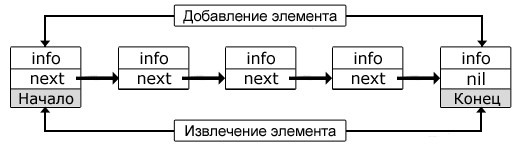
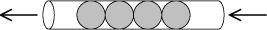Дек (двусторонняя очередь).
Дек (deque — double ended queue, «двусторонняя очередь») – структура данных типа «список», функционирующая одновременно по двум принцам организации данных: FIFO и LIFO. Определить дек можно как очередь с двумя сторонами, так и стек, имеющий два конца. То есть данный подвид списка характерен двухсторонним доступом: выполнение поэлементной операции, определенной над деком, предполагает возможность выбора одной из его сторон в качестве активной.
Число основных операций, выполняемых над стеком и очередью, как помнит читатель, равнялось трем: добавление элемента, удаление элемента, чтение элемента. При этом не указывалось место структуры данных, активное в момент их выполнения, поскольку ранее оно однозначно определялось свойствами (определением) самой структуры. Теперь, ввиду дека как обобщенного случая, для приведенных операций следует указать эту область. Разделив каждую из операций на две: одну применительно к «голове» дека, другую – его «хвосту», получим набор из шести операций:
На практике этот список может быть дополнен проверкой дека на пустоту, получением его размера и некоторыми другими операциями.
В плане реализации двусторонняя очередь очень близка к стеку и обычной очереди: в качестве ее базиса приемлемо использовать как массив, так и список. Далее мы напишем интерфейс обработки дека, представленного обычным индексным массивом. Программа будет состоять из основной части и девяти функций:
Помимо самого массива потребуется указатель на последний элемент, назовем его last. Указатель на первый элемент не потребуется, поскольку дек будет представлять собой смещающуюся структуру, т. е. при добавлении нового элемента в начало, каждый из старых элементов сместиться на одну позицию вправо, уступив тем самым первому элементу ячейку с индексом 0 (в C++), следовательно, адрес первого элемента – константа.
Алгоритмы и структуры данных для начинающих: стеки и очереди
Авторизуйтесь
Алгоритмы и структуры данных для начинающих: стеки и очереди
В предыдущих частях мы рассматривали базовые структуры данных, которые, по сути, являлись надстройками над массивом. В этой статье мы добавим к коллекциям простые операции и посмотрим, как это повлияет на их возможности.
Стек — это коллекция, элементы которой получают по принципу «последний вошел, первый вышел» (Last-In-First-Out или LIFO). Это значит, что мы будем иметь доступ только к последнему добавленному элементу.
25–26 ноября, Москва и онлайн, От 24 000 до 52 000 ₽
Наиболее часто встречающаяся аналогия для объяснения стека — стопка тарелок. Вне зависимости от того, сколько тарелок в стопке, мы всегда можем снять верхнюю. Чистые тарелки точно так же кладутся на верх стопки, и мы всегда будем первой брать ту тарелку, которая была положена последней.
Если мы положим, например, красную тарелку, затем синюю, а затем зеленую, то сначала надо будет снять зеленую, потом синюю, и, наконец, красную. Главное, что надо запомнить — тарелки всегда ставятся и на верх стопки. Когда кто-то берет тарелку, он также снимает ее сверху. Получается, что тарелки разбираются в порядке, обратном тому, в котором ставились.
Теперь, когда мы понимаем, как работает стек, введем несколько терминов. Операция добавления элемента на стек называется «push», удаления — «pop». Последний добавленный элемент называется верхушкой стека, или «top», и его можно посмотреть с помощью операции «peek». Давайте теперь посмотрим на заготовку класса, реализующего стек.
Класс Stack
Метод Push
Поскольку мы используем связный список для хранения элементов, можно просто добавить новый в конец списка.
Метод Pop
Push добавляет элементы в конец списка, поэтому забирать их будет также с конца. В случае, если список пуст, будет выбрасываться исключение.
Метод Peek
Метод Count
Зачем нам знать, сколько элементов находится в стеке, если мы все равно не имеем к ним доступа? С помощью этого поля мы можем проверить, есть ли элементы на стеке или он пуст. Это очень полезно, учитывая, что метод Pop кидает исключение.
Пример: калькулятор в обратной польской записи
Классический пример использования стека — калькулятор в обратной польской, или постфиксной, записи. В ней оператор записывается после своих операндов. То есть, мы пишем:
Другими словами, вместо «4 + 2» мы запишем «4 2 +». Если вам интересно происхождение обратной польской записи и ее названия, вы можете узнать об этом на Википедии или в поисковике.
То, как вычисляется обратная польская запись и почему стек так полезен при ее использовании, хорошо видно из следующего алгоритма:
То есть, для выражения «4 2 +» действия будут следующие:
В конце на стеке окажется одно значение — 6.
Очередь
Очереди очень похожи на стеки. Они также не дают доступа к произвольному элементу, но, в отличие от стека, элементы кладутся (enqueue) и забираются (dequeue) с разных концов. Такой метод называется «первый вошел, первый вышел» (First-In-First-Out или FIFO). То есть забирать элементы из очереди мы будем в том же порядке, что и клали. Как реальная очередь или конвейер.
Очереди часто используются в программах для реализации буфера, в который можно положить элемент для последующей обработки, сохраняя порядок поступления. Например, если база данных поддерживает только одно соединение, можно использовать очередь потоков, которые будут, как ни странно, ждать своей очереди на доступ к БД.
Класс Queue
Метод Enqueue
Новые элементы очереди можно добавлять как в начало списка, так и в конец. Важно только, чтобы элементы доставались с противоположного края. В данной реализации мы будем добавлять новые элементы в начало внутреннего списка.
Метод Dequeue
Поскольку мы вставляем элементы в начало списка, убирать мы их будем с конца. Если список пуст, кидается исключение.
Метод Peek
Метод Count
Двусторонняя очередь
Двусторонняя очередь (Double-ended queue), или дек (Deque), расширяет поведение очереди. В дек можно добавлять или удалять элементы как с начала, так и с конца очереди. Такое поведение полезно во многих задачах, например, планирование выполнения потоков или реализация других структур данных. Позже мы рассмотрим вариант реализации стека с помощью двусторонней очереди.
Класс Deque
Метод EnqueueFirst
Метод EnqueueLast
Метод DequeueFirst
Метод DequeueLast
Метод PeekFirst
Метод PeekLast
Метод Count
Пример: реализация стека
Двусторонняя очередь часто используется для реализации других структур данных. Давайте посмотрим на пример реализации стека с ее помощью.
У вас, возможно, возник вопрос, зачем реализовывать стек на основе очереди вместо связного списка. Причины две: производительность и повторное использование кода. У связного списка есть накладные расходы на создание узлов и нет гарантии локальности данных: элементы могут быть расположены в любом месте памяти, что вызывает большое количество промахов и падение производительности на уровне процессоров. Более производительная реализация двусторонней очереди требует массива для хранения элементов.
Тем не менее, реализация стека или очереди с помощью массива — непростая задача, но такая реализация двусторонней очереди и использование ее в качестве основы для других структур данных даст нам серьезный плюс к производительности и позволит повторно использовать код. Это снижает стоимость поддержки.
Позже мы посмотрим на вариант очереди с использованием массива, но сначала давайте взглянем на класс стека с использованием двусторонней очереди:
Хранение элементов в массиве
Как уже было упомянуто, у реализации очереди с использованием массива есть свои преимущества. Она выглядит простой, но на самом деле есть ряд нюансов, которые надо учесть.
Давайте посмотрим на проблемы, которые могут возникнуть, и на их решение. Кроме того, нам понадобится информация об увеличении внутреннего массива из прошлой статьи о динамических массивах.
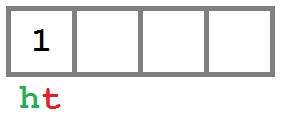
При создании очереди у нее внутри создается массив нулевой длины. Красные буквы «h» и «t» означают указатели _head и _tail соответственно.
Добавляем элемент в начало
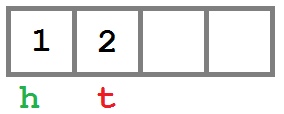
Добавляем элемент в конец
Добавляем еще один элемент в начало
Обратите внимание: индекс «головы» очереди перескочил в начало списка. Теперь первый элемент, который будет возвращен при вызове метода DequeueFirst — 0 (индекс 3).
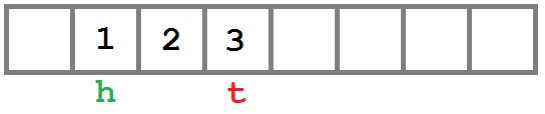
И еще один в конец
Массив заполнен, поэтому при добавлении элемента произойдет следующее:
Добавляем значение в конец расширенного массива
Теперь посмотрим, что происходит при удалении элемента:
Удаляем элемент из начала
Удаляем элемент с конца
Ключевой момент: вне зависимости от вместимости или заполненности внутреннего массива, логически, содержимое очереди — элементы от «головы» до «хвоста» с учетом «закольцованности». Такое поведение также называется «кольцевым буфером».
Теперь давайте посмотрим на реализацию.
Класс Deque (с использованием массива)
Интерфейс очереди на основе массива такой же, как и в случае реализации через связный список. Мы не будем его повторять. Однако, поскольку список был заменен на массив, у нас добавились новые поля — сам массив, его размер и указатели на «хвост» и «голову» очереди.
Алгоритм роста
Когда свободное место во внутреннем массиве заканчивается, его необходимо увеличить, скопировать элементы и обновить указатели на «хвост» и «голову». Эта операция производится при необходимости во время добавления элемента. Параметр startingIndex используется, чтобы показать, сколько полей в начале необходимо оставить пустыми (в случае добавления в начало).
Обратите внимание на то, как извлекаются данные, когда приходится переходить в начало массива при проходе от «головы» к «хвосту».
Метод EnqueueFirst
Метод EnqueueLast
Метод DequeueFirst
Метод DequeueLast
Метод PeekFirst
Метод PeekLast
Метод Count
Продолжение следует
Вот мы и закончили четвертую часть нашего цикла статей. В ней мы рассмотрели стеки и очереди. В следующий раз мы перейдем к бинарным деревьям поиска.
Структуры данных
Теоретический материал: стеки, очереди, деки (С++)
Стек, очередь, дек
(англ. ) называется хранилище данных, в котором можно работать только с одним элементом: тем, который был добавлен в стек последним. Стек должен поддерживать следующие операции:
push Добавить (положить) в конец стека новый элемент
pop Извлечь из стека последний элемент
back Узнать значение последнего элемента (не удаляя его)
size Узнать количество элементов в стеке
clear Очистить стек (удалить из него все элементы)
Реализуйте структуру данных «стек», реализовав все указанные здесь методы. Напишите программу (функцию main ), содержащую описание стека и моделирующую работу стека. Функция main считывает последовательность команд и в зависимости от команды выполняет ту или иную операцию. После выполнения одной команды программа должна вывести одну строчку. Возможные команды для программы:
Гарантируется, что набор входных команд удовлетворяет следующим требованиям: максимальное количество элементов в стеке в любой момент не превосходит 100, все команды pop_back и back корректны, то есть при их исполнении в стеке содержится хотя бы один элемент.
Пример протокола работы программы
Пример протокола работы программы
Реализуйте стек динамического размера, то есть ограниченный только объемом свободной оперативной памяти. Для этого используйте указатели и динамически распределяемую память. Если для полностью заполненного стека вызывается метод push размер динамического массива, отведенного для хранения стека, должен увеличиваться.
Очередь
Очередью (aнгл. )) называется структура данных, в которой элементы кладутся в конец, а извлекаются из начала. Таким образом, первым из очереди будет извлечен тот элемент, который будет добавлен раньше других.
Элементы очереди будем также хранить в массиве. При этом из очереди удаляется первый элемент, и, чтобы не сдвигать все элементы очереди, будем в отдельном поле m_start хранить индекс элемента массива, с которого начинается очередь. При удалении элементов, очередь будет «ползти» дальше от начала массива. Чтобы при этом не происходил выход за границы массива, замкнем массив в кольцо: будем считать, что за последним элементом массива следует первый.
Описание структуры очередь:
Аналогично заданию C, но для очереди. Необходимо реализовать очередь, память для которой динамически выделяется при увеличении количества элементов в ней.
push_front Добавить (положить) в начало дека новый элемент
push_back Добавить (положить) в конец дека новый элемент
pop_front Извлечь из дека первый элемент
pop_back Извлечь из дека последний элемент
front Узнать значение первого элемента (не удаляя его)
back Узнать значение последнего элемента (не удаляя его)
size Узнать количество элементов в деке
clear Очистить дек (удалить из него все элементы)
Как и зачем делать очередь на двух стеках
Данный пост написан для новичков в олимпиадном программировании и начинающих разработчиков, готовящихся к прохождению алгоритмических интервью. В конце бонусная задачка. Если заинтересовал, прошу под кат 
Для начала вспомним основы:
Стек реализует принцип LIFO (англ. last in — first out, «последним пришёл — первым вышел»).
Стек имеет две основные операции:
Очередь
Очередь — это структура данных с доступом к элементам FIFO (англ. First In, First Out – «первым пришёл — первым ушёл»)
Очередь имеет два основных метода в своем интерфейсе:
Обычно рассматривают два базовых подхода к реализации очереди:
Почему стек круче, чем очередь
Представим себе, что наша структура данных должна поддерживать следующий набор операций:
Для стека можно очень просто поддерживать любую из приведенных операций: достаточно хранить на его вершине пару:
, где второй элемент пары — результат операции, примененной ко всем элементам стека.
Ниже пример реализации стека с поддержкой минимума на Python:
А теперь подумайте, как проделать тот же фокус с очередью? Если пробовать с классической очередью, организованной на массиве, вряд ли что-то получится. Это связано с тем, что операция минимум не имеет обратную операцию (как операция сложения имеет операцию вычитания, например). Как вы могли догадаться, далее я расскажу о не совсем классической реализации очереди на двух стеках.
Очередь на двух стеках
Главное условие, которое должно быть выполнено — все операции должны выполняться за амортизированное O(1).
Возьмем два стека: s1 и s2.
Операцию push будем всегда делать в стек s1.
Операция pop будет устроена так: если стек s2 пустой, перекладываем все элементы из s1 в s2 последовательными вызовами pop и push. Теперь в стеке s2 лежат элементы в обратном порядке (самый верхний элемент — это самый первый положенный элемент в нашу очередь).
Если s2 не пуст, тупо достаем элементы из него. Как только s2 окажется снова пустым повторяем ту же операцию.
Время работы
Операция push: Мы тупо кладем элемент в стек s1. Время работы O(1).
Операция pop: Для каждого элемента мы делаем не более одного перекладывания из стека в стек, следовательно амортизированное время работы составит O(1).
Операция get_min: Для стеков s1 и s2 известны минимумы, поэтому мы просто берем минимум из минимумов. Время работы O(1).
Бонусная задачка
Заключение
Спасибо, что дочитали до конца!
Если вас заинтересовала тема, можете почитать как сделать персистентную очередь на двух стеках здесь, либо дождаться выхода следующего моего топика.
Пишите в комментариях какие задачи на двух стеках вам приходилось решать на интервью или контестах.
Структуры данных: общее понятие, реализация. Простейшие структуры данных: очередь, стек. Использование стека и обратная польская запись
Простейшие структуры данных. Стек. Очередь
Очередь
Очередь как структура данных понятна даже людям, не знакомым с программированием. Очередь содержит элементы, как бы выстроенные друг за другом в цепочку. У очереди есть начало и конец. Добавлять новые элементы можно только в конец очереди, забирать элементы можно только из начала. В отличие от обычной очереди, которую всегда можно при желании покинуть, из середины программистской очереди удалять элементы нельзя.
Очередь можно представить в виде трубки. В один конец трубки можно добавлять шарики — элементы очереди, из другого конца они извлекаются. Элементы в середине очереди, т.е. шарики внутри трубки, недоступны. Конец трубки, в который добавляются шарики, соответствует концу очереди, конец, из которого они извлекаются — началу очереди. Таким образом, концы трубки не симметричны, шарики внутри трубки движутся только в одном направлении.
В принципе, можно было бы разрешить добавлять элементы в оба конца очереди и забирать их также из обоих концов. Такая структура данных в программировании тоже существует, ее название — » дек «, от англ. Double Ended Queue, т.е. очередь с двумя концами. Дек применяется значительно реже, чем очередь.
Использование очереди в программировании почти соответствует ее роли в обычной жизни. Очередь практически всегда связана с обслуживанием запросов, в тех случаях, когда они не могут быть выполнены мгновенно. Очередь поддерживает также порядок обслуживания запросов. Рассмотрим, к примеру, что происходит, когда человек нажимает клавишу на клавиатуре компьютера. Тем самым человек просит компьютер выполнить некоторое действие. Например, если он просто печатает текст, то действие должно состоять в добавлении к тексту одного символа и может сопровождаться перерисовкой области экрана, прокруткой окна, переформатированием абзаца и т.п.
Любая, даже самая простая, операционная система всегда в той или иной степени многозадачна. Это значит, что в момент нажатия клавиши операционная система может быть занята какой-либо другой работой. Тем не менее, операционная система ни в какой ситуации не имеет права проигноровать нажатие на клавишу. Поэтому происходит прерывание работы компьютера, он запоминает свое состояние и переключается на обработку нажатия на клавишу. Такая обработка должна быть очень короткой, чтобы не нарушить выполнение других задач. Команда, отдаваемая нажатием на клавишу, просто добавляется в конец очереди запросов, ждущих своего выполнения. После этого прерывание заканчивается, компьютер восстанавливает свое состояние и продолжает работу, которая была прервана нажатием на клавишу. Запрос, поставленный в очередь, будет выполнен не сразу, а только когда наступит его черед.
Реализация очереди на базе массива
Стек — самая популярная и, пожалуй, самая важная структура данных в программировании. Стек представляет собой запоминающее устройство, из которого элементы извлекаются в порядке, обратном их добавлению. Это как бы неправильная очередь, в которой первым обслуживают того, кто встал в нее последним. В программистской литературе общепринятыми являются аббревиатуры, обозначающие дисциплину работы очереди и стека. Дисциплина работы очереди обозначается FIFO, что означает первым пришел — первым уйдешь (First In First Out). Дисциплина работы стека обозначается LIFO, последним пришел — первым уйдешь (Last In First Out).
Стек можно представить в виде трубки с подпружиненым дном, расположеной вертикально. Верхний конец трубки открыт, в него можно добавлять, или, как говорят, заталкивать элементы. Общепринятые английские термины в этом плане очень красочны, операция добавления элемента в стек обозначается push, в переводе «затолкнуть, запихнуть». Новый добавляемый элемент проталкивает элементы, помещеные в стек ранее, на одну позицию вниз. При извлечении элементов из стека они как бы выталкиваются вверх, по-английски pop («выстреливают»).
Примером стека может служить стог сена, стопка бумаг на столе, стопка тарелок и т.п. Отсюда произошло название стека, что по-английски означает стопка. Тарелки снимаются со стопки в порядке, обратном их добавлению. Доступна только верхняя тарелка, т.е. тарелка на вершине стека. Хорошим примером будет также служить железнодорожный тупик, в который можно составлять вагоны.
Использование стека в программировании
Стек применяется довольно часто, причем в самых разных ситуациях. Объединяет их следующая цель: нужно сохранить некоторую работу, которая еще не выполнена до конца, при необходимости переключения на другую задачу. Стек используется для временного сохранения состояния не выполненного до конца задания. После сохранения состояния компьютер переключается на другую задачу. По окончании ее выполнения состояние отложенного задания восстанавливается из стека, и компьютер продолжает прерванную работу.
В Фортране-4, одном из самых старых и самых удачных языков программирования, аргументы передаются через специальную область памяти, которая может располагаться не в стеке, поскольку до конца 70-х годов XX века еще существовали компьютеры вроде IBM 360 или ЕС ЭВМ без аппаратной реализации стека. Адреса возврата также сохранялись не в стеке, а в фиксированных для каждой подпрограммы ячейках памяти. Программисты называют такую память статической в том смысле, что статические переменные занимают всегда одно и то же место в памяти в любой момент работы программы. При использовании только статической памяти рекурсия невозможна, поскольку при новом вызове предыдущие значения локальных переменных разрушаются. В эталонном Фортране-4 использовались только статические переменные, а рекурсия была запрещена. До сих пор язык Фортран широко используется в научных и инженерных расчетах, однако, современный стандарт Фортрана-90 уже вводит стековую память, устраняя недостатки ранних версий языка.
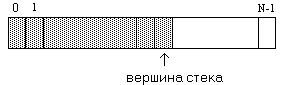
Реализация стека на базе массива
Реализация стека на базе массива является классикой программирования. Иногда даже само понятие стека не вполне корректно отождествляется с этой реализацией.
Когда стек пуст, указатель стека содержит значение минус единица. При добавлении элемента указатель стека сначала увеличивается на единицу, затем в ячейку массива с индексом, содержащимся в указателе стека, записывается добавляемый элемент. При извлечении элемента из стека сперва содержимое ячейки массива с индексом, содержащимся в указателе стека, запоминается во временной переменной в качестве результата операции, затем указатель стека уменьшается на единицу.