Что такое графы в программировании
Степень входа вершины – количество входящих в нее ребер, степень выхода – количество исходящих ребер.

Классификация графов
В связном графе между любой парой вершин существует как минимум один путь.
В несвязном графе существует хотя бы одна вершина, не связанная с другими.
Графы также подразделяются на
В ориентированном графе ребра являются направленными, т.е. существует только одно доступное направление между двумя связными вершинами.
В неориентированном графе по каждому из ребер можно осуществлять переход в обоих направлениях.
Частный случай двух этих видов – смешанный граф. Он характерен наличием как ориентированных, так и неориентированных ребер.
Способы представления графа
Граф может быть представлен (сохранен) несколькими способами:
Использование двух первых методов предполагает хранение графа в виде двумерного массива (матрицы). Размер массива зависит от количества вершин и/или ребер в конкретном графе.
Матрица смежности графа — это квадратная матрица, в которой каждый элемент принимает одно из двух значений: 0 или 1.
Число строк матрицы смежности равно числу столбцов и соответствует количеству вершин графа.

Когда из одной вершины в другую проход свободен (имеется ребро), в ячейку заносится 1, иначе – 0. Все элементы на главной диагонали равны 0 если граф не имеет петель.
Матрица инцидентности (инциденции) графа — это матрица, количество строк в которой соответствует числу вершин, а количество столбцов – числу рёбер. В ней указываются связи между инцидентными элементами графа (ребро(дуга) и вершина).
В неориентированном графе если вершина инцидентна ребру то соответствующий элемент равен 1, в противном случае элемент равен 0.
Матрица инцидентности для своего представления требует нумерации рёбер, что не всегда удобно.
Список смежности (инцидентности)
Если количество ребер графа по сравнению с количеством вершин невелико, то значения большинства элементов матрицы смежности будут равны 0. При этом использование данного метода нецелесообразно. Для подобных графов имеются более оптимальные способы их представления.
По отношению к памяти списки смежности менее требовательны, чем матрицы смежности. Такой список можно представить в виде таблицы, столбцов в которой – 2, а строк — не больше, чем вершин в графе.
В каждой строке в первом столбце указана вершина выхода, а во втором столбце – список вершин, в которые входят ребра из текущей вершины.
Преимущества списка смежности:
Недостатки списка смежности:
Алгоритмы обхода графов
Основными алгоритмами обхода графов являются
Поиск в ширину подразумевает поуровневое исследование графа:
Вершины просматриваются в порядке возрастания их расстояния от корня.
Алгоритм прекращает свою работу после обхода всех вершин графа, либо в случае выполнения требуемого условия (например, найти кратчайший путь из вершины 1 в вершину 6).
Каждая вершина может находиться в одном из 3 состояний:
Фиолетовый – рассматриваемая вершина. 
Применения алгоритма поиска в ширину
Алгоритм поиска в ширину работает как на ориентированных, так и на неориентированных графах.
Для реализации алгоритма удобно использовать очередь.
Реализация на C++ (с использованием очереди STL)
Результат выполнения
Задача поиска кратчайшего пути
Реализация на С++
Поиск в глубину – это алгоритм обхода вершин графа.
Поиск в ширину производится симметрично (вершины графа просматривались по уровням). Поиск в глубину предполагает продвижение вглубь до тех пор, пока это возможно. Невозможность продвижения означает, что следующим шагом будет переход на последний, имеющий несколько вариантов движения (один из которых исследован полностью), ранее посещенный узел (вершина).
Отсутствие последнего свидетельствует об одной из двух возможных ситуаций:
Каждая вершина может находиться в одном из 3 состояний:
Фиолетовый – рассматриваемая вершина. 
Применения алгоритма поиска в глубину
Алгоритм поиска в глубину работает как на ориентированных, так и на неориентированных графах. Применимость алгоритма зависит от конкретной задачи.
Для реализации алгоритма удобно использовать стек или рекурсию.
Реализация на C++ (с использованием стека STL)
Результат выполнения 
Задача поиска лексикографически первого пути на графе.
Реализация на C++
Результат выполнения 
Поиск в глубину также может быть реализован с использованием рекурсивного алгоритма.
Реализация обхода графа в глубину на C++ (с использованием рекурсии)
Графы: основы теории, алгоритмы поиска
Aug 22, 2020 · 6 min read
Возможно, вы уже знакомы с понятием спортивного программирования и знаете, что оно помогает развить навыки решения проблем и прокачать технические знания о структурах данных и алгоритмах.
Одной из важнейших составляющих спортивного программирования является изучение алгоритмов. В этой статье мы охватим большое количество алгоритмов, в том числе все алгоритмы на графах, знание которых понадобится вам для успешного решения задач из теории графов на соревнованиях по программированию. Конечно, одних теоретических знаний алгоритмов недостаточно, и вам придётся набить руку в решении практических задач на таких сайтах, как Codeforces. Настоящая же статья представит вам инструменты, необходимые для освоения важных графовых алгоритмов. Итак, приступим.
Что такое граф?
Г р афы, в понимании программистов, — это не те графики, которые мы изучали в школе. Это не столбиковые диаграммы или гистограммы.
С точки зрения компьютерных наук и дискретной математики, графы — это абстрактный способ представления типов отношений, например дорог, соединяющих города, и других видов сетей. Графы состоят из рёбер и вершин. Вершина — это точка на графе, а ребро — это то, что соединяет две точки на графе.
В условиях задач из теории графов на соревнованиях по программированию обычно говорится о таких вещах, как сети и решётки.
Вот список всех терминов, относящихся к теории графов, которые вам нужно знать:
Представление графов в коде
Для того, чтобы использовать алгоритмы на графах в коде, сначала нам нужно разобраться, как осуществляется представление графов в коде. Весь следующий код будет на C++, так как для спортивного программирования я предпочитаю именно этот язык за его скорость и встроенные функции, позволяющие упростить написание решений задач.
Будут показаны два способа представления графов: матрицы смежности и списки смежности. Больше вам пригодится представление графов в виде списка смежности.
Матрицы смежности
Матрица смежности представляет собой граф в виде двумерной матрицы с размерами V x V, где V — количество вершин графа. Матрицы смежности лучше всего применять, когда V² примерно равно E (числу рёбер), то есть когда граф плотный. Запись a_ij обозначает, сколько рёбер соединяют вершину i и вершину j.
Списки смежности
Другой распространенный способ представления графов в коде — списки смежности. Суть в том, что вы создаёте списки соседей для каждой вершины, а затем помещаете все эти списки в другой список. Их лучше всего применять, когда в графе небольшое количество рёбер, то есть когда граф разрежённый. Если у вас взвешенный граф, т.е. каждое ребро графа имеет какой-то вес, то в списке будут содержаться пары для рёбер (сосед, вес).
Поиск в глубину
Теперь, когда мы научились представлять графы в коде, можем приступить к изучению некоторых алгоритмов на графах! Начнём с поиска в глубину (DFS) и завершим поиском в ширину (BFS). Чтобы не загромождать статью, алгоритмы поиска пути не будут здесь рассматриваться (интересующиеся могут ознакомиться с алгоритмом поиска кратчайшего пути Беллмана-Форда).
Поиск в глубину — это один из базовых алгоритмов на графах. Он применяется для поиска расстояния от одной вершины до других вершин в графе. Это алгоритм обхода.
Поиск в глубину помечает каждую вершину в графе одной из двух меток: посещённая или не посещённая. Алгоритм помечает каждую вершину как посещённую, если удаётся избежать циклов. Он работает следующим образом:
Поиск в ширину
Поиск в ширину — ещё один алгоритм обхода графов. Вместе с алгоритмом поиска вглубь он составит большую часть увлекательных соревнований по программированию, по крайней мере, тех из них, что относятся к графам.
Поиск в ширину тоже помещает каждую вершину в графе в одну из двух категорий: посещённых или непосещённых. И цель у обоих алгоритмов одна и та же: помечать каждую вершину в графе как посещённую, если удаётся избежать циклов. Вот как работает алгоритм поиска в ширину:
Как видите, алгоритм поиска в ширину очень похож на алгоритм поиска в глубину. Однако вместо того, чтобы спускаться вниз по ветви графа или дерева, как это делает алгоритм поиска в глубину, алгоритм поиска в ширину проходит каждый уровень.
Заключение
Освоив теоретическую часть, касающуюся двух самых важных алгоритмов обхода на графах, вам остаётся только практиковаться, чтобы использовать эти алгоритмы в соревнованиях по программированию. Я бы порекомендовал для начала Codeforces: решайте задачи, помеченные тегами bfs и dfs с рейтингом до 1400. Когда почувствуете, что справляетесь с ними, увеличьте сложность.
Отработка навыков решения алгоритмических задач, особенно алгоритмов на графах, поможет вам побеждать на соревнованиях по программированию и успешно проходить технические собеседования. Вперёд — к успехам!
Графы: основы теории, алгоритмы поиска
Возможно, вы уже знакомы с понятием спортивного программирования и знаете, что оно помогает развить навыки решения проблем и прокачать технические знания о структурах данных и алгоритмах.
Одной из важнейших составляющих спортивного программирования является изучение алгоритмов. В этой статье мы охватим большое количество алгоритмов, в том числе все алгоритмы на графах, знание которых понадобится вам для успешного решения задач из теории графов на соревнованиях по программированию. Конечно, одних теоретических знаний алгоритмов недостаточно, и вам придётся набить руку в решении практических задач на таких сайтах, как Codeforces. Настоящая же статья представит вам инструменты, необходимые для освоения важных графовых алгоритмов. Итак, приступим.
Что такое граф?
Графы, в понимании программистов, — это не те графики, которые мы изучали в школе. Это не столбиковые диаграммы или гистограммы.
С точки зрения компьютерных наук и дискретной математики, графы — это абстрактный способ представления типов отношений, например дорог, соединяющих города, и других видов сетей. Графы состоят из рёбер и вершин. Вершина — это точка на графе, а ребро — это то, что соединяет две точки на графе.
В условиях задач из теории графов на соревнованиях по программированию обычно говорится о таких вещах, как сети и решётки.
Вот список всех терминов, относящихся к теории графов, которые вам нужно знать:
Представление графов в коде
Для того, чтобы использовать алгоритмы на графах в коде, сначала нам нужно разобраться, как осуществляется представление графов в коде. Весь следующий код будет на C++, так как для спортивного программирования я предпочитаю именно этот язык за его скорость и встроенные функции, позволяющие упростить написание решений задач.
Будут показаны два способа представления графов: матрицы смежности и списки смежности. Больше вам пригодится представление графов в виде списка смежности.
Матрицы смежности
Матрица смежности представляет собой граф в виде двумерной матрицы с размерами V x V, где V — количество вершин графа. Матрицы смежности лучше всего применять, когда V² примерно равно E (числу рёбер), то есть когда граф плотный. Запись a_ij обозначает, сколько рёбер соединяют вершину i и вершину j.
Списки смежности
Другой распространенный способ представления графов в коде — списки смежности. Суть в том, что вы создаёте списки соседей для каждой вершины, а затем помещаете все эти списки в другой список. Их лучше всего применять, когда в графе небольшое количество рёбер, то есть когда граф разрежённый. Если у вас взвешенный граф, т.е. каждое ребро графа имеет какой-то вес, то в списке будут содержаться пары для рёбер (сосед, вес).
Поиск в глубину
Теперь, когда мы научились представлять графы в коде, можем приступить к изучению некоторых алгоритмов на графах! Начнём с поиска в глубину (DFS) и завершим поиском в ширину (BFS). Чтобы не загромождать статью, алгоритмы поиска пути не будут здесь рассматриваться (интересующиеся могут ознакомиться с алгоритмом поиска кратчайшего пути Беллмана-Форда).
Поиск в глубину — это один из базовых алгоритмов на графах. Он применяется для поиска расстояния от одной вершины до других вершин в графе. Это алгоритм обхода.
Поиск в глубину помечает каждую вершину в графе одной из двух меток: посещённая или не посещённая. Алгоритм помечает каждую вершину как посещённую, если удаётся избежать циклов. Он работает следующим образом:
Поиск в ширину
Поиск в ширину — ещё один алгоритм обхода графов. Вместе с алгоритмом поиска вглубь он составит большую часть увлекательных соревнований по программированию, по крайней мере, тех из них, что относятся к графам.
Поиск в ширину тоже помещает каждую вершину в графе в одну из двух категорий: посещённых или непосещённых. И цель у обоих алгоритмов одна и та же: помечать каждую вершину в графе как посещённую, если удаётся избежать циклов. Вот как работает алгоритм поиска в ширину:
Как видите, алгоритм поиска в ширину очень похож на алгоритм поиска в глубину. Однако вместо того, чтобы спускаться вниз по ветви графа или дерева, как это делает алгоритм поиска в глубину, алгоритм поиска в ширину проходит каждый уровень.
Заключение
Освоив теоретическую часть, касающуюся двух самых важных алгоритмов обхода на графах, вам остаётся только практиковаться, чтобы использовать эти алгоритмы в соревнованиях по программированию. Я бы порекомендовал для начала Codeforces: решайте задачи, помеченные тегами bfs и dfs с рейтингом до 1400. Когда почувствуете, что справляетесь с ними, увеличьте сложность.
Отработка навыков решения алгоритмических задач, особенно алгоритмов на графах, поможет вам побеждать на соревнованиях по программированию и успешно проходить технические собеседования. Вперёд — к успехам!
Распознавание и представление графов. Часть 1
Jun 5, 2018 · 7 min read
Введение
Графы представляют собой фундаментальные структуры данных в программировании. Как правило, имеется множество различных способов решений задач с графами. Например, это могут быть задачи, связаны с поиском пути на двумерном графе (между начальной и конечной точками), или поиском максимального количества жидкости, которое может пройти через трубопровод, если известна максимальная пропускная способность каждого участка трубопровода (эта задача также известна в качестве задачи о максимальном потоке или задачи о минимизации отходов при раскрое, которые мы будет рассматривать позднее). Понимание структур данных при решении задач на графах имеет решающее значение. Подчас решение, казалось бы неразрешимой задачи, при использовании подходящей структуры данных может представлять несколькими строками кода, и к счастью стандартные библиотеки языков программирования могут нам оказать здесь неоценимую помощь!
Идентификация задач на графах
Первым шагом к решению задач, связанных с графами, является идентификация типа задач, решаемых с помощью графов. При знакомстве с проблемой на практике бывает сразу трудно усмотреть такую связь. Поэтому при анализе важно обратить внимание возможные упоминания в условиях каких-либо сетей. Если явные упоминания отсутствуют, следует поискать косвенные ссылки, например, постановка проблема может требовать найти путь или маршрут. В этом случае метод решения задачи непосредственно связан с применением графов. В качестве ориентиров также следует обратить внимание на некоторые ключевые слова, используемые в постановке задач, решаемых с помощью графов — это такие термины как вершины, узлы, ребра, соединения, соединения, пути, циклы, направление. Вот простой пример постановки проблемы:
«Боб потерялся в своем районе и ему нужно вернуться обратно домой. Район Боба — это равномерная двумерная сетка, которая начинается в точке (0, 0) и далее описывается следующими параметрами: ширина клетки сетки равна 1, высота — 1. На сетке располагаются пустые пространства, через которые Боб может пройти без труда, и места, занятые домами, через которые Боб не может пройти. Боб может двигаться только по горизонтали или по вертикали на один квадрат за один шаг (момент времени).
Обозначим начальное положение Боба точкой «B», а расположение дома точкой «H». Пустые квадраты на сетке обозначим точками «.», а дома — крестиком «X». Необходимо найти минимальное количество шагов, которые потребуются Бобу для возвращения домой, а если Боб не сможет вернуться домой, необходимо возвратить значение «-1».
Вот пример окрестности шириной 7 и высотой 5 клеток сети:
Как только вы поняли, что данная задача относится к теории графов, приступайте к созданию представления графа в памяти компьютера.
Представление графа и ключевые понятия
В реальности графы могут представляться множеством различных систем, начиная с двумерной сетки (как в вышеприведенной задаче), заканчивая картой интернета, которая показывает, сколько времени требуется для переноса данных с компьютера А на компьютер B. Сначала нужно определить элементы, из которых состоит граф. В действительности таких элементов всего два — это узлы и ребра. Узел (или вершина) — это фиксированная точка на графе. Ребро (или соединение) — это связующее звено между двумя вершинами, которое может быть направленным (ориентированное ребро) или не направленным (неориентированное ребро), также ребру может быть приписана численная характеристика (например, стоимость). Неориентированное ребро означает отсутствие ограничений на направление, к котором можно проходить через ребро между узлами. Так, например, по неориентированному ребру между узлами A и B можно проходить как в направлении от A к B так и от B к A. Ориентированное ребро допускает перемещение только в одном направлении, поэтому, например, для направленного ребра от A к B можно передвигаться только из вершины A в вершину B, но не наоборот, от B в A. Наиболее простым представлением о ребрах и вершинах является следующее: ребро — это функция двух вершин, возвращающая стоимость. Рассмотрим пример такого подхода.
Если пользоваться математической нотацией для обозначения графа, то можно определить его как G =
Односвязные списки
Примером одного из простейших типов графов является односвязный список! Рассмотрим преимущества графовой структуры данных, с помощью которой можно описывать как очень сложные отношения, так и весьма простые, например, список.
У односвязного списка есть один «корневой» узел, и каждый узел ссылается на следующий узел. Таким образом, структура выглядит так:
Можно привести следующий простой пример:
Графически это можно было бы представить как корень->B->C->null. Здесь null представляет собой конец списка.
Вернемся к концепции функции стоимости. Наша функция стоимости может выглядеть следующим образом:
Такая функция стоимости показывает, что мы можем перейти непосредственно от одного узла к другому через ребро. Вам нужно привыкнуть к использованию функции затрат, поскольку каждый раз, когда вы будете сталкиваться с графами, в той или иной форме вы будете иметь дело с функцией затрат! В данный момент у вас может возникнуть вопрос: «Подождите секундочку, для пути от A до C функция стоимости может не существовать, хотя фактически, я могу добраться до C от A, пройдя через B!» Это действительно так, но дело в том, что функция стоимости просто хранит непосредственно стоимость кратчайшего пути при движении от одного узла к другому. Позже мы рассмотрим, как найти расстояния в на графах общего типа.
Теперь, когда мы рассмотрели пример одного из самых простых типов графов, перейдем к более сложным примерам.
Деревья
Далее для подробного рассмотрения деревьев мы отводим отдельный раздел. Сейчас пока кратко рассмотрим их в качестве примера. Выше мы были несколько ограничены в представляемом типе данных. Например, если вы захотите создать генеалогическое древо (иерархическую организацию родственных связей), вы не сможете сохранить более одного родителя для каждого ребенка. Поэтому, очевидно, нужен новый тип структуры данных. Новая структура узла будет выглядеть примерно так:
С функцией стоимости:
Здесь видно, что у каждого узла имеется и мать и отец. Узел позволяет рекурсивно определить структуру в целом — у каждой матери есть свои мать и отец и у каждого отца, также есть свои мать и отец, и так далее. Здесь может возникнуть такая проблема как образование циклов, если вы захотите описать эту структуру данных на компьютере. Но дерево не может содержать петель. Это очевидно, если задуматься над следующим вопросом: является ли отец одновременно и сыном своего ребенка? У меня уже начала болеть голова :). Поэтому вы должны быть очень осторожны при построении дерева — каждый раз вам следует убедиться, что это действительно древовидная структура, а не граф более общего вида. Более формальное определение дерева таково: дерево — это связный граф без циклов. Это означает, что каждый узел графа соединяется, по меньшей мере, с одним узлом графа.
Еще одно замечание: можно легко представить ситуацию, когда дерево требует более двух ребер между узлами, например, в случае описания организационной иерархии — у вас может иметься менеджер, который управляет несколькими подчиненными, тогда как генеральный директор также управляет несколькими менеджерами. Наш пример ‑ это пример графа, известного как двоичное дерево, поскольку имеется только две связи с узлами. Далее перейдем к построению структуры данных, которая может представлять граф общего вида!
Графы
Дерево допускает для узла только наличие потомков и в дереве отсутствуют циклы, для графа общего вида возможно представление более богатого выбора ситуаций. Весьма распространенным примером является маршрут перелета между городами. Если рассматривается рейс между городом А и городом В, это означает что между этими городами можно провести ребро. Стоимостью ребра может являться время, которое потребуется для выполнения перелета, или, например, расход топлива.
Способ представления для этой задачи заключается в описании ребер между узлами (или вершинами) с другими узлами, а также с помощью приписанных узлам параметров. Таким образом, для примера перелета мы могли бы описать аэропорт как узел, и тогда для каждого вылета из города у нас имеется соседний узел, являющийся пунктом назначения.
Это пример общего способа представления графа. Такое описание допускает наличие нескольких ребер, исходящих из одного узла к другому, что позволяет очень компактно описать графа. Однако недостатком здесь является большая трудность работы с таким представлением, по сравнению, например, с методом массива, обсуждаемым далее.
Представление массива
Метод представления графа в виде списка узлов очень удобен. Но обычно topcoder накладывает на нас определенные ограничения, чтобы облегчить жизнь. Мы рассматриваем небольшие графы, содержащие малое количество узлов и ребер. В такой ситуации мы можем воспользоваться другим типом структуры данных, с которым легче работать.
Для примера, ниже представлена следующая матрица связей:
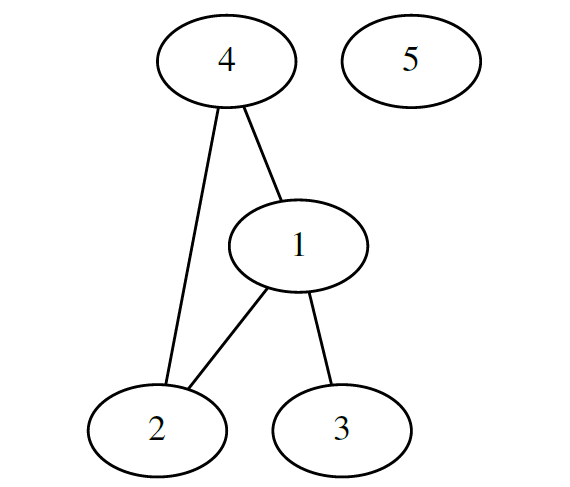
Это означает, что вес связи узла А с самим сбой (цикл) равен нулю, единица — это вес связи с узлом B, а 5 ‑ вес связи с узлом C. Узел B, с другой стороны, не имеет связи с узлом A, а вес его связи с узлом C равен 1. Узел C ни к одному из узлов не подключен. Если вы нарисуете этот граф, он будет выглядеть так:
Такое представление удобно для графов, которые не содержат нескольких ребер между каждым из узлов, что позволяет значительно упростить работу.















