что такое список в программировании

Список

Связный список (англ. List) — структура данных, состоящая из элементов, содержащих помимо собственных данных ссылки на следующий и/или предыдущий элемент списка. С помощью списков можно реализовать такие структуры данных как стек и очередь.

Содержание

Односвязный список [ править ]

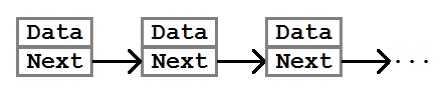
Простейшая реализация списка. В узлах хранятся данные и указатель на следующий элемент в списке.

Двусвязный список [ править ]

Также хранится указатель на предыдущий элемент списка, благодаря чему становится проще удалять и переставлять элементы.

XOR-связный список [ править ]

В некоторых случаях использование двусвязного списка в явном виде является нецелесообразным. В целях экономии памяти можно хранить только результат выполнения операции Xor над адресами предыдущего и следующего элементов списка. Таким образом, зная адрес предыдущего элемента, мы можем вычислить адрес следующего элемента.

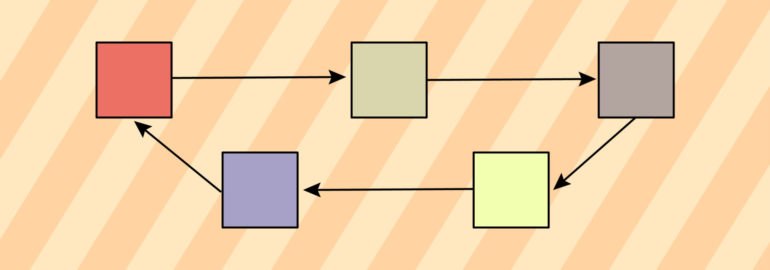
Циклический список [ править ]

Первый элемент является следующим для последнего элемента списка.

Операции на списке [ править ]

Рассмотрим базовые операции на примере односвязного списка.

Вставка [ править ]

Очевиден случай, когда необходимо добавить элемент ( [math]newHead[/math] ) в голову списка. Установим в этом элементе ссылку на старую голову, и обновим указатель на голову.

Поиск [ править ]

Удаление [ править ]

Для того, чтобы удалить голову списка, переназначим указатель на голову на второй элемент списка, а голову удалим.

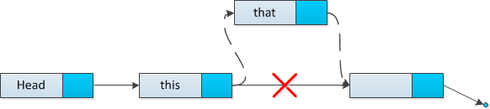
Удаление элемента после заданного ( [math]thisElement[/math] ) происходит следующим образом: изменим ссылку на следующий элемент на следующий за удаляемым, затем удалим нужный объект.

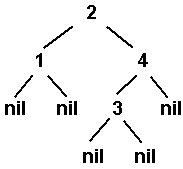
Поиск цикла в списке [ править ]

Для начала необходимо уметь определять — список циклический или нет. Воспользуемся алгоритмом Флойда «Черепаха и заяц». Пусть за одну итерацию первый указатель (черепаха) переходит к следующему элементу списка, а второй указатель (заяц) на два элемента вперед. Тогда, если эти два указателя встретятся, то цикл найден, если дошли до конца списка, то цикла нет.

Поиск длины хвоста в списке с циклом [ править ]

Наивные реализации [ править ]

Реализация за [math]O(n^2)[/math] [ править ]

Будем последовательно идти от начала цикла и проверять, лежит ли этот элемент на цикле. На каждой итерации запустим от [math]pointMeeting[/math] вперёд указатель. Если он окажется в текущем элементе, прежде чем посетит [math]pointMeeting[/math] снова, то точку окончания (начала) хвоста нашли.

Реализация за [math]O(n \log n)[/math] [ править ]

Эффективная реализация [ править ]

Доказательство корректности алгоритма [ править ]

[math]f_1(n) = L + (n-L) \bmod N[/math]

[math]f_2(n) = L + (2n-L) \bmod N[/math]

[math]Q = L + (1-k) N[/math]

Пусть [math]L = p N + M, 0 \leqslant M \lt N[/math]

[math]L \lt k N \leqslant L + N[/math]

[math]pN + M \lt kN \leqslant (p+1)N + M[/math] откуда [math]k = p + 1[/math]

Задача про обращение списка [ править ]

Для того, чтобы обратить список, необходимо пройти по всем элементам этого списка, и все указатели на следующий элемент заменить на предыдущий. Эта рекурсивная функция принимает указатель на голову списка и предыдущий элемент (при запуске указывать [math]NULL[/math] ), а возвращает указатель на новую голову списка.

Алгоритм корректен, поскольку значения элементов в списке не изменяются, а все указатели [math]next[/math] изменят свое направление, не нарушив связности самого списка.

Источник

Алгоритмы и структуры данных для начинающих: связный список

Авторизуйтесь

Алгоритмы и структуры данных для начинающих: связный список

Первая структура данных, которую мы рассмотрим — связный список. На то есть две причины: первое — связный список используется практически везде — от ОС до игр, и второе — на его основе строится множество других структур данных.

Связный список

Основное назначение связного списка — предоставление механизма для хранения и доступа к произвольному количеству данных. Как следует из названия, это достигается связыванием данных вместе в список.

Прежде чем мы перейдем к рассмотрению связного списка, давайте вспомним, как хранятся данные в массиве.

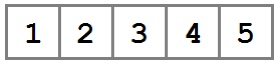
Как показано на рисунке, данные в массиве хранятся в непрерывном участке памяти, разделенном на ячейки определенного размера. Доступ к данным в ячейках осуществляется по ссылке на их расположение — индексу.

Это отличный способ хранить данные. Большинство языков программирования позволяют так или иначе выделить память в виде массива и оперировать его содержимым. Последовательное хранение данных увеличивает производительность (data locality), позволяет легко итерироваться по содержимому и получать доступ к произвольному элементу по индексу.

Тем не менее, иногда массив — не самая подходящая структура.

Предположим, что у нашей программы следующие требования:

Поскольку в требованиях указано, что считанные числа передаются в метод ProcessItems за один раз, очевидным решение будет массив целых чисел:

У этого решения есть ряд проблем, но самая очевидная из них — что случится, если будет необходимо прочесть больше 20 значений? В данной реализации значения с 21 и далее просто проигнорируются. Можно выделить больше памяти — 200 или 2000 элементов. Можно дать пользователю возможность выбрать размер массива. Или выделить память под новый массив большего размера при заполнении старого и скопировать элементы. Но все эти решения усложняют код и бесполезно тратят память.

Нам нужна коллекция, которая позволяет добавить произвольное число элементов и перебрать их в порядке добавления. Размер коллекции должен быть неограничен, а произвольный доступ нам не нужен. Нам нужен связный список.

Прежде чем перейти к его реализации, давайте посмотрим на то, как могло бы выглядеть решение нашей задачи.

Обратите внимание: проблем, присущих первому варианту решения больше нет — мы не можем выделить недостаточно или, наоборот, слишком много памяти под массив.

Кроме того, из этого кода можно увидеть, что наш список будет принимать параметр типа и реализовывать интерфейс IEnumerable

Реализация класса LinkedList

Класс Node

В основе связного списка лежит понятие узла, или элемента (Node). Узел — это контейнер, который позволяет хранить данные и получать следующий узел.

В самом простом случае класс Node можно реализовать так:

Класс LinkedList

Прежде чем реализовывать наш связный список, нужно понять, как мы будем с ним работать.

Ранее мы увидели, что коллекция должна поддерживать любой тип данных, а значит, нам нужно реализовать обобщенный интерфейс.

Учитывая все вышесказанное, давайте набросаем примерный план класса, а затем заполним недостающие методы.

Метод Add

Добавление элемента в связный список производится в три этапа:

Основная сложность заключается в том, чтобы найти последний узел списка. Можно сделать это двумя способами. Первый — сохранять указатель на первый узел списка и перебирать узлы, пока не дойдем до последнего. В этом случае нам не требуется сохранять указатель на последний узел, что позволяет использовать меньше памяти (в зависимости от размера указателя на вашей платформе), но требует прохода по всему списку при каждом добавлении узла. Это значит, что метод Add займет O(n) времени.

Второй метод заключается в сохранении указателя на последний узел списка, и тогда при добавлении нового узла мы поменяем указатель так, чтобы он указывал на новый узел. Этот способ предпочтительней, поскольку выполняется за O(1) времени.

Первое, что нам необходимо сделать — добавить два приватных поля в класс LinkedList : ссылки на первый (head) и последний (tail) узлы.

Теперь мы можем добавить метод, который выполняет три необходимых шага.

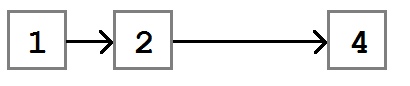
Метод Remove

После удаления узла поле Next узла со значением «2» будет указывать на узел со значением «4».

Основной алгоритм удаления элемента такой:

Как всегда, основная проблема кроется в мелочах. Вот некоторые из случаев, которые необходимо предусмотреть:

Поле Count декрементируется при удалении узла.

Метод Contains

Метод GetEnumerator

Метод Clear

Метод CopyTo

Метод CopyTo проходит по списку и копирует элементы в массив с помощью присваивания. Клиент, вызывающий метод должен убедиться, что массив имеет достаточный размер для того, чтобы вместить все элементы списка.

Метод Count

Метод IsReadOnly

Двусвязный список

Связный список, который мы только что создали, называется также «односвязным». Это значит, что между узлами только одна связь в единственном направлении от первого узла к последнему. Есть также достаточно распространенный вариант списка, который предоставляет доступ к обоим концам — двусвязный список.

Далее мы рассмотрим только отличия в реализации односвязного и двусвязного списка.

Класс Node

Единственное изменение, которое надо внести в класс LinkedListNode — добавить поле со ссылкой на предыдущий узел.

Метод AddFirst

При добавлении элемента в начало списка последовательность действий примерно такая же, как и при добавлении элемента в односвязный список.

Метод AddLast

Метод RemoveFirst

Метод RemoveLast

Метод Remove

Зачем нужен двусвязный список?

Так мы сможем итерироваться по списку вручную, в том числе от последнего элемента к первому.

В этом примере мы используем поля Tail и Previous для того, чтобы обойти список задом наперед.

Кроме того, двусвязный список позволяет легко реализовать двусвязную очередь, которая, в свою очередь, является строительным блоком для других структур данных. Мы вернемся к ней позже, в соответствующей части.

Продолжение следует

На этом мы заканчиваем разбор связных списков. В следующий раз мы подробно разберем массивы.

Источник

Динамические структуры данных: однонаправленные и двунаправленные списки

Цель лекции: изучить понятия, классификацию и объявление списков, особенности доступа к данным и работу с памятью при использовании однонаправленных и двунаправленных списков, научиться решать задачи с использованием списков на языке C++.

Понятие списка хорошо известно из жизненных примеров: список студентов учебной группы, список призёров олимпиады, список (перечень) документов для представления в приёмную комиссию, список почтовой рассылки, список литературы для самостоятельного чтения и т.п.

В основном они отличаются видом взаимосвязи элементов и/или допустимыми операциями.

Однонаправленные (односвязные) списки

Описание простейшего элемента такого списка выглядит следующим образом:

struct имя_типа поле ; адресное поле ; >;

где информационное поле – это поле любого, ранее объявленного или стандартного, типа;

адресное поле – это указатель на объект того же типа, что и определяемая структура, в него записывается адрес следующего элемента списка.

Информационных полей может быть несколько.

Основными операциями, осуществляемыми с однонаправленными списками, являются:

Особое внимание следует обратить на то, что при выполнении любых операций с линейным однонаправленным списком необходимо обеспечивать позиционирование какого-либо указателя на первый элемент. В противном случае часть или весь список будет недоступен.

Рассмотрим подробнее каждую из приведенных операций.

Для описания алгоритмов этих основных операций используется следующее объявление:

Создание однонаправленного списка

Печать (просмотр) однонаправленного списка

Источник

Список (программирование)

В информатике, спи́сок (англ. list ) — это абстрактный тип данных, представляющий собой упорядоченный набор значений, в котором некоторое значение может встречаться более одного раза. Экземпляр списка является компьютерной реализацией математического понятия конечной последовательности. Экземпляры значений, находящихся в списке, называются элементами списка (англ. item, entry либо element ); если значение встречается несколько раз, каждое вхождение считается отдельным элементом.

Термином список также называется несколько конкретных структур данных, применяющихся при реализации абстрактных списков, особенно связных списков.

Содержание

Определение

При помощи нотации метода синтаксически-ориентированного конструирования Ч. Хоара определение списка можно записать следующим образом:

Свойства

У определённой таким образом структуры данных имеются некоторые свойства:

Списки используются для хранения наборов однотипных элементов. Такие элементы могут быть отсортированы для использования в функциях поиска или функциях для быстрой вставки новых элементов в список.

Списки в языках программирования

Функциональные языки

Списки в функциональных языках являются фундаментальной структурой. Большинство функциональных языков имеет встроенные средства для работы со списками вроде получения длины списка, головы (первый элемент списка), хвоста (часть списка, идущая за первым элементом), применения функции к каждому элементу списка (Map), свертки списка и пр.

Источник

Программирование списков

На практике часто встречаются задачи, связанные с перечислением объектов. В некоторых случаях при решении задач важно сохранять ин­фор­ма­цию об уже сделанных шагах решения, чтобы их не повторять. Такую операцию удобно реализовывать помощью списков.

Список — это простая структура данных, широко используется в не­чис­­ловом программировании. Список представляет собой после­до­ва­тель­ность, составленную из произвольного числа элементов.

Например, перечисление объектов: Мери, Джон, Том, Анн можно записать так:

Элементами списка могут быть любые структуры.

Первый элемент называется головой списка, остальная часть — хвостом. Например, для списка

a — это голова, а хвостом является список [b, c, d, e]. Для представления пустого списка используется [].

На практике часто бывает удобным трактовать хвост списка как самостоятельный объект, используется вертикальная черта, отделяющую голову от хвоста:

Можно определить список рекурсивно.

Список — это структура данных, определяемая следующим образом:

Определение списка через его голову и хвост в сочетании с рекурсией ле­жит в основе большого числа программ, оперирующих со списками. Эти про­грам­мы состоят:

Перед использованием списка в программе его необходимо описать.

Для того чтобы использовать предикат к спискам различного типа, необходимо описать один и тот же предикат для всех типов списков.

Предположим, что есть база данных с фактами о разных людях, и каждый факт связывает имя человека и его массу. Если необходимо объединить данные о массе всех людей в единой списковой переменной L, то используется стандартный предикат findall.

Пример 1. Принадлежность элемента списку.

Составление программы для отношения принадлежности может быть основано на следующих соображениях:

а) X есть голова L, либо

б) X принадлежит хвосту L

Применять member можно в двух направлениях

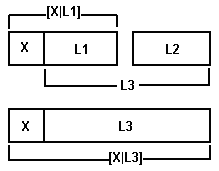
Пример 2. Соединение двух списков.

Для написания программы удобно воспользоваться графическим представлением.

Необходимо рассмотреть два случая:

Пример 3. Удаление элемента из списка.

Отношение delete можно определить аналогично принадлежности:

Отношение delete недетерминированно.

Пример 4. Перестановки.

Иногда бывает полезно построить все перестановки некоторого заданного списка. Для решения удобно воспользоваться графическим представлением:

Источник