Перевод из десятичной системы счисления в двоичную
Перед тем как перейти к алгоритму перевода, вспомним алфавит двоичной и десятичной системы счисления:
| Основание | Название | Алфавит |
|---|---|---|
| 2 | Двоичная | 0, 1 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Для перевода чисел из десятичной системы в двоичную, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.
Алгоритм перевода целых десятичных чисел в двоичную систему счисления
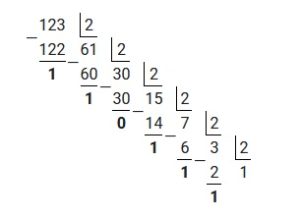
Пример 1 : перевести десятичное число 123 в двоичную систему счисления
Для наглядности произведем деление «столбиком». Решение будет выглядеть следующим образом:
Исходя из вышеприведенного алгоритма, полученные остатки необходимо записать в обратном порядке.
Алгоритм перевода десятичной дроби в двоичную систему
Пример 2: перевести число 0,123 в двоичную систему.
Решение будет выглядеть следующим образом:
0.123 ∙ 2 = 0.246 (0)
0.246 ∙ 2 = 0.492 (0)
0.492 ∙ 2 = 0.984 (0)
0.984 ∙ 2 = 1.968 (1)
0.968 ∙ 2 = 1.936 (1)
0.936 ∙ 2 = 1.872 (1)
0.872 ∙ 2 = 1.744 (1)
0.744 ∙ 2 = 1.488 (1)
0.488 ∙ 2 = 0.976 (0)
0.976 ∙ 2 = 1.952 (1)
0.952 ∙ 2 = 1.904 (1)
В данном примере можно продолжить вычисления, но зачастую, такой точности будет достаточно.
Перевод дробного десятичного числа в двоичную систему
Для того чтобы перевести десятичное число, содержащее дробную часть, необходимо отдельно перевести целую часть и отдельно дробную.
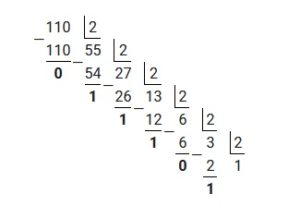
Пример 3: перевести число 110,625 из десятичной системы в двоичную
Для решения примера потребуется отдельно перевести 110 и отдельно 0,625 из десятичной системы в двоичную, используя вышеизложенные алгоритмы. Таким образом переведя 110, получим:
Перевод десятичной дроби 0,625 выглядит так:
0.625 ∙ 2 = 1.25 (1)
0.25 ∙ 2 = 0.5 (0)
0.5 ∙ 2 = 1 (1)
Теперь осталось соединить результаты перевода. Таким образом: 110.62510=1101110.1012
Обратите внимание, что данный пример наглядно демонстрирует ситуацию, при которой дробная часть стала равной 0 и дальнейшее вычисление закончилось.
Перевод чисел из одной системы счисления в другую
Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.
Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.
Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
20010 = 110010002 = 3108 = C816
Кратко об основных системах счисления
Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.
Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.
Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.
Перевод в десятичную систему счисления
Перевод из десятичной системы счисления в другие
Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в восьмеричную систему:
Перевод из двоичной системы в восьмеричную
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
Перевод из двоичной системы в шестнадцатеричную
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Перевод из восьмеричной системы в двоичную
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Используем таблицу триад:
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
Перевод из шестнадцатеричной системы в двоичную
Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.
Десятичный код.
К примеру, десятичное число 31110 в двоичной системе счисления записано будет в двоичном коде так : 1 0011 01112, в двоично-десятичном коде оно будет записано как 0001 0001BCD.
Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн.
В формате BCD из Unsigned Integer простой способ получения данных такой:
Число «A» в формате U16 = 542,
теперь, выполнив преобразование его в BCD (проделать операцию можно на калькуляторе ОС Windows) получаем :
Особенности десятичного кода.
Из преимуществ двоично-десятичного кода можно выделить такие:
— Упрощены операции умножения или деления на 10, а также округление.
Учитывая все эти преимущества, формат двоично-десятичного кода применяется в калькуляторах, ведь в простейших арифметических операциях, калькулятор должен в точности такой же самый выводить результат, какой человек подсчитает на бумаге.
Кроме достоинств, двоично-десятичный код имеет и свои характерные недостатки: требуется больше памяти и усложнены арифметические операции. Так как, вместо 16 в в 8421-BCD используются только 10 возможных комбинаций 4-х битового поля, поэтому при операциях сложения и вычитания чисел в формате 8421-BCD действуют такие правила:
— Каждый раз при сложении двоично-десятичных чисел, когда в старший полубайт происходит перенос бита, необходимо добавить корректирующее значение 0110 (= 610 = 1610 — 1010: разница количеств используемых значений и комбинаций полубайта) к тому полубайту, от которого был произведен перенос.
— Когда встречается комбинация недопустимая для полубайта то необходимо добавить с разрешением переноса в старшие полубайты к каждой недопустимой комбинации корректирующее значение 0110, каждый раз при выполнении сложения двоично-десятичных чисел.
— Для каждого полубайта, который получил заем из старшего полубайта, при вычитании двоично-десятичных чисел, необходимо провести коррекцию, для этого нужно отнять значение 0110.
Операция по сложению двоично-десятичных чисел на примере выглядит так: Задача: Определить число A = D + C, где D = 3927, C = 4856
Решение: Числа D и C представим в виде двоично-десятичного кода:
1000 0111 1000 0011
Двоично-десятичная система счисления
Обозначение смешанной системы счисления
В мире электронно-вычислительных технологий существуют различные системы счислений. Одним из классов систем счисления является класс смешанной системы счисления.
Таких систем существует несколько, одной из них является двоично-десятичная система счисления.
Построение в двоично-десятичной системе
В этой записи используются четверки цифр двоично-десятичной системы, которые последовательно отображают цифры 9, 2 и 5. Эти последовательные четверки цифр называются тетрадами.
В двоичной системе для изображения чисел также используются 0 и 1, но невзирая на это, изображения десятичного числа в двоично-десятичной системе отличается от его записи в двоичной системе счисления. К примеру, та же запись 100100100101 в этих двух системах будет обозначать разное десятичное число. Это выглядит так:
Подобное изображение числа зачастую используется в качестве вспомогательного этапа при трансформации числа из двоичной в десятичную систему счисления и наоборот. В двоично-десятичной системе счисления алгоритмы арифметических вычислений многозначных чисел намного сложнее, чем в простых системах счисления, но тем не менее эта система счисления часто используется для этих операций в микросхемах компьютеров и калькуляторов.
Сложно разобраться самому?
Попробуй обратиться за помощью к преподавателям
При корректировке результатов элементарных арифметических операций с числами, записанными с помощью двоично-десятичных кодов, используют специальные команды для преобразования их в двоично-десятичную систему счисления. В данном случае применяется правило: для получения в результате простой арифметической операции сложения или вычитания число в тетраде, большее чем 9, к ней нужно прибавить число 6. Такое уравновешивание по разрядам производится обычно с помощью двоично-десятичной системы счисления. При этом самым целесообразным является комплексное использование двоичной и двоично-десятичной систем счисления, так как при этом количество тактов уравновешивания намного меньшее, чем при использовании иных систем счисления.
Для чего нужно использование двоично-десятичной системы счисления
Человеческому глазу понятна десятичная система изображения чисел, и мы используем ее практически в любой сфере жизни, где сталкиваемся с числами. Работа электроники построена на использовании двоичной системы вывода чисел. Поэтому вариант применения системы счисления с помощью двоично-десятичных кодов является компромиссным. Двоично-десятичные коды используется в тех микросхемах приборов, где есть потребность частого ввода и вывода десятичных чисел, к примеру, в электронных часах, калькуляторах, таймерах, дисплеях бытовой техники и прочих приборах, в которых нет смысла использовать универсальные микрокоды из-за ограниченного объема памяти.
В арифметических логических устройствах электронно-вычислительных машин есть специальные блоки арифметических вычислений, выполняющих операции на основании двоично-десятичной системы счисления. Во многих случаях это существенно повышает производительность электронно-вычислительных машин. Например, если рассмотреть системы автоматизированной обработки данных, в которых практически не используются арифметические вычисления, то процесс трансформации чисел из одной системы в другую занял бы длительный ресурс времени и памяти. Поэтому в микропроцессорах в таком случае применяются двоичные коды, но при этом они умеют распознавать команды трансформации в двоично-десятичные коды. В итоге результат изображается на дисплее в десятичной форме изображения числа, понятной человеку.
Выгоды применения двоично-десятичной системы
Применение двоично-десятичной системы счисления в комплексе с двоичной системой, которая является одной из основных, позволяет создавать на рынке высокопроизводительные электронно-вычислительные машины. Это становится возможным благодаря применению блока десятичных арифметических операций без необходимости программного трансформирования чисел в двоичную систему.
Не нашли что искали?
Просто напиши и мы поможем
Трансформация чисел в двоично-десятичную систему из десятичной не требует громоздких арифметических вычислений, а является простой операцией с использованием четырехразрядных кодов тетрад, что производится автоматически при помощи элементарных алгоритмических программ.
Так как две двоично-десятичные цифры в сумме занимают всего 1 байт памяти, то с его помощью можно записать любую десятичную цифру от 0 до 99. Таким образом, используя всего лишь 1 байт для изображения двух любых десятичных цифр, возможно записать любое количество двоично-десятичных чисел с необходимым количеством десятичных разрядов.
Не нашли нужную информацию?
Закажите подходящий материал на нашем сервисе. Разместите задание – система его автоматически разошлет в течение 59 секунд. Выберите подходящего эксперта, и он избавит вас от хлопот с учёбой.
Гарантия низких цен
Все работы выполняются без посредников, поэтому цены вас приятно удивят.
Доработки и консультации включены в стоимость
В рамках задания они бесплатны и выполняются в оговоренные сроки.
Вернем деньги за невыполненное задание
Если эксперт не справился – гарантируем 100% возврат средств.
Тех.поддержка 7 дней в неделю
Наши менеджеры работают в выходные и праздники, чтобы оперативно отвечать на ваши вопросы.
Тысячи проверенных экспертов
Мы отбираем только надёжных исполнителей – профессионалов в своей области. Все они имеют высшее образование с оценками в дипломе «хорошо» и «отлично».
Гарантия возврата денег
Эксперт получил деньги, а работу не выполнил?
Только не у нас!
Деньги хранятся на вашем балансе во время работы над заданием и гарантийного срока
Гарантия возврата денег
В случае, если что-то пойдет не так, мы гарантируем возврат полной уплаченой суммы
Отзывы студентов о нашей работе




























«Всё сдал!» — безопасный онлайн-сервис с проверенными экспертами
Используя «Всё сдал!», вы принимаете пользовательское соглашение
и политику обработки персональных данных
Сайт работает по московскому времени:
Принимаем к оплате 


Запись десятичных чисел (двоично-десятичный код)
Иногда бывает удобно хранить числа в памяти процессора в десятичном виде (Например, для вывода на экран дисплея). Для записи таких чисел используются двоично-десятичные коды. Не нужно путать двоично-десятичный код с десятичной системой счисления. Для записи одного десятичного разряда используется четыре двоичных бита. Эти четыре бита называются тетрадой. Иногда встречается название, пришедшее из англоязычной литературы: нибл. При помощи четырех бит можно закодировать шестнадцать цифр. Лишние комбинации в двоично-десятичном коде являются запрещенными. Таблица соответствия двоично-десятичного кода и десятичных цифр приведена ниже:
| Двоично-десятичный код | Десятичный код | |||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 2 |
| 0 | 0 | 1 | 1 | 3 |
| 0 | 1 | 0 | 0 | 4 |
| 0 | 1 | 0 | 1 | 5 |
| 0 | 1 | 1 | 0 | 6 |
| 0 | 1 | 1 | 1 | 7 |
| 1 | 0 | 0 | 0 | 8 |
| 1 | 0 | 0 | 1 | 9 |
Остальные комбинации двоичного кода в тетраде являются запрещенными. Запишем пример двоично-десятичного кода:
В первой тетраде записана цифра 1, во второй — 2, в третьей — 5, а в последней тетраде записана цифра 8. В данном примере для записи числа 1258 потребовалось четыре тетрады. Количество ячеек памяти микропроцессора зависит от его разрядности. При 16-разрядном процессоре все число уместится в одну ячейку памяти.
В данном примере для записи числа достаточно трех тетрад, но ячейка памяти 16-разрядная. Поэтому старшая тетрада заполняется нулями. Они не изменяют значение цифры. Если бы мы заполнили нулями младшую тетраду, то число увеличилось бы в десять раз!
При записи десятичных чисел часто требуется записывать знак числа и десятичную запятую (в англоязычных странах точку). Двоично-десятичный код часто применяется для набора телефонного номера или набора кодов телефонных служб. В этом случае кроме десятичных цифр часто применяются символы ‘*’ или ‘#’. Для записи этих символов в двоично-десятичном коде применяются запрещенные комбинации
| Двоично-десятичный код | Дополнительный символ | |||
|---|---|---|---|---|
| 1 | 0 | 1 | 0 | * (звёздочка) |
| 1 | 0 | 1 | 1 | # (решётка) |
| 1 | 1 | 0 | 0 | + (плюс) |
| 1 | 1 | 0 | 1 | – (минус) |
| 1 | 1 | 1 | 0 | , (десятичная запятая) |
| 1 | 1 | 1 | 1 | Символ гашения |
Достаточно часто в памяти процессора для хранения одной десятичной цифры выделяется одна ячейка памяти (восьми, шестнадцати или тридцатидвухразрядная). Это делается для повышения скорости работы программы. Для того, чтобы отличить такой способ записи двоично-десятичного числа от стандартного, способ записи десятичного числа, как это показано в примере, называется упакованной формой двоично-десятичного числа. Запишем те же числа, что и в предыдущем примере в неупакованном двоично-десятичном коде для восьмиразрядного процессора:
Суммирование двоично-десятичных чисел.
Понравился материал? Поделись с друзьями!
Другие виды двоичных кодов:
Целочисленные двоичные коды Представление двоичных чисел в памяти компьютера или микроконтроллера
https://digteh.ru/proc/IntCod.php
Представление чисел в двоичном коде с плавающей запятой Стандартные форматы чисел с плавающей запятой для компьютеров и микроконтроллеров
https://digteh.ru/proc/float/
Запись текстов двоичным кодом Представление текстов в памяти компьютеров и микроконтроллеров
https://digteh.ru/proc/text/
Системы счисления В настоящее время и в технике и в быту широко используются как позиционные, так и непозиционные системы счисления.
https://digteh.ru/digital/SysSchis.php
Предыдущие версии сайта:
http://neic.nsk.su/
Об авторе:
к.т.н., доц., Александр Владимирович Микушин
Кандидат технических наук, доцент кафедры САПР СибГУТИ. Выпускник факультета радиосвязи и радиовещания (1982) Новосибирского электротехнического института связи (НЭИС).
А.В.Микушин длительное время проработал ведущим инженером в научно исследовательском секторе НЭИС, конструкторско технологическом центре «Сигнал», Научно производственной фирме «Булат». В процессе этой деятельности он внёс вклад в разработку систем радионавигации, радиосвязи и транкинговой связи.
Научные исследования внедрены в аппаратуре радинавигационной системы Loran-C, комплексов мобильной и транкинговой связи «Сигнал-201», авиационной системы передачи данных «Орлан-СТД», отечественном развитии системы SmarTrunkII и радиостанций специального назначения.