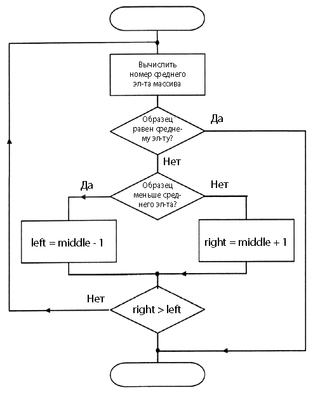
Бинарный поиск
Бинарный поиск производится в упорядоченном массиве.
При бинарном поиске искомый ключ сравнивается с ключом среднего элемента в массиве. Если они равны, то поиск успешен. В противном случае поиск осуществляется аналогично в левой или правой частях массива.
Алгоритм может быть определен в рекурсивной и нерекурсивной формах.
Количество шагов поиска определится как
где n-количество элементов,
↑ — округление в большую сторону до ближайшего целого числа.
На каждом шаге осуществляется поиск середины отрезка по формуле
mid = (left + right)/2
Если искомый элемент равен элементу с индексом mid, поиск завершается.
В случае если искомый элемент меньше элемента с индексом mid, на место mid перемещается правая граница рассматриваемого отрезка, в противном случае — левая граница.
left = 0, right = 19
mid = (19+0)/2=9
Сравниваем значение по этому индексу с искомым:
mid = (9+19)/2=14
Сравниваем значение по этому индексу с искомым:
84 > 82
Сдвигаем правую границу:
right = mid = 14
mid = (9+14)/2=11
Сравниваем значение по этому индексу с искомым:
mid = (11+14)/2=12
Сравниваем значение по этому индексу с искомым:
mid = (12+14)/2=13
Сравниваем значение по этому индексу с искомым:
82 = 82
Решение найдено!
Чтобы уменьшить количество шагов поиска можно сразу смещать границы поиска на элемент, следующий за серединой отрезка:
left = mid + 1
right = mid — 1
Целочисленный двоичный поиск
Целочисленный двоичный поиск (бинарный поиск) (англ. binary search) — алгоритм поиска объекта по заданному признаку в множестве объектов, упорядоченных по тому же самому признаку, работающий за логарифмическое время.
| Задача: |
| Пусть нам дан упорядоченный массив, состоящий только из целочисленных элементов. Требуется найти позицию, на которой находится заданный элемент. |
Содержание
Принцип работы [ править ]
Двоичный поиск заключается в том, что на каждом шаге множество объектов делится на две части и в работе остаётся та часть множества, где находится искомый объект. Или же, в зависимости от постановки задачи, мы можем остановить процесс, когда мы получим первый или же последний индекс вхождения элемента. Последнее условие — это левосторонний/правосторонний двоичный поиск.
Правосторонний/левосторонний целочисленный двоичный поиск [ править ]
Использовав эти два вида двоичного поиска, мы можем найти отрезок позиций [math][l,r][/math] таких, что [math]\forall i \in [l,r] : a[i] = x[/math] и [math] \forall i \notin [l,r] : a[i] \neq x [/math]
Пример: [ править ]
Если искомого элемента в массиве нет, то правосторонний поиск выдаст максимальный элемент, меньший искомого, а левосторонний наоборот, минимальный элемент, больший искомого.
Алгоритм двоичного поиска [ править ]
Код [ править ]
Несколько слов об эвристиках [ править ]
Эвристика с завершением поиска, при досрочном нахождении искомого элемента
Заметим, что если нам необходимо просто проверить наличие элемента в упорядоченном множестве, то можно использовать любой из правостороннего и левостороннего поиска. При этом будем на каждой итерации проверять «не попали ли мы в элемент, равный искомому», и в случае попадания заканчивать поиск.
Эвристика с запоминанием ответа на предыдущий запрос
Применение двоичного поиска на некоторых неотсортированных массивах [ править ]
| Задача: |
| Массив образован путем приписывания в конец массива, отсортированного по возрастанию, массива, отсортированного по убыванию. Требуется максимально быстро найти элемент в таком массиве. |
Время выполнения алгоритма — [math] O(\log n)[/math] (так как и бинарный поиск, и тернарный поиск работают за логарифмическое время с точностью до константы).
| Задача: |
| Два отсортированных по возрастанию массива записаны один в конец другого. Требуется максимально быстро найти элемент в таком массиве. |
Мы имеем массив, образованный из двух отсортированных подмассивов, записанных один в конец другого. Запустить сразу бинарный или тернарный поиски на таком массиве нельзя, так как массив не будет обязательно отсортированным и он не будет иметь [math]1[/math] точку экстремума. Поэтому попробуем найти индекс последнего элемента левого массива, чтобы потом запустить бинарный поиск два раза на отсортированных массивах.
| Задача: |
| Массив образован путем циклического сдвига массива, образованного приписыванием отсортированного по убыванию массива в конец отсортированного по возрастанию. Требуется максимально быстро найти элемент в таком массиве. |
В случае же убывание-возрастание-убывание ( [math] \searrow \nearrow \searrow [/math] ) может быть, что будет неправильно найден минимум. Найдем правильный минимум аналогично поиску максимума в предыдущем абзаце.
Затем, в зависимости от типа нашего массива, запустим бинарный поиск три раза на каждом промежутке.
Переполнение индекса середины [ править ]
Бинарный поиск в C++: подробное руководство
Сегодня мы и изучим его. Также попытаемся ответить на такие вопросы: как бинарный поиск работает в программе, плюсы и минусы его использования у себя в коде и в каких структурах данных можно его применять, а в каких нет. Поехали!
Что такое бинарный поиск
Линейный поиск по сравнению с бинарным — дешевая подделка. Бинарный поиск — очень быстрый алгоритм с не сложной реализацией, который находит элемент с определенным значением в уже отсортированном массиве.
Очень важно помнить! Алгоритм будет работать правильно, только с отсортированным массивом. А если по случайности вы забыли отсортировать массив перед его использованием, то в большинстве случаев тот ответ, который подсчитал алгоритм, будет неверным.
Принцип работы бинарного поиска
Самым легким и самым долгим по времени решением, будет поочередная проверка пассажиров в комнате с прибором (это линейный поиск). Но это слишком долго.
В задаче выше охранники использовали алгоритм двоичного поиска для нахождения диверсанта. В обычной программе принцип работы бинарного поиска такой же, как и в примере, выше.
Как создать бинарный поиск в C++
Давайте посмотрим как работает бинарный поиск на примере.В примере ниже в строке 9 мы создали массив arr на 10 элементов и в строке 12 предложили пользователю с клавиатуры заполнить его ячейки.
В строке 20 мы предлагаем пользователю ввести ключ (который нужно будет найти в массиве), а дальше мы с бинарным поиском проверим массив на наличие введенного ключа пользователем. Если мы найдем ключ в массиве, то выведем индекс ячейки, в которой находится ключ.
Я не могу написать бинарный поиск
Недавно (буквально два года назад) тут пробегала статья Только 10% программистов способны написать двоичный поиск. Двоичный поиск — это классический алгоритм поиска. Мало того, это еще чрезвычайно простой алгоритм, который можно очень легко описать: берем отсортированный массив, смотрим в середину, если не нашли там число, в зависимости от того, что в середине — ищем это число этим же методом либо в левой части, либо в правой, откидывая средний элемент. Для функций также, просто берем не массив, а функцию. Все очень и очень просто, алгоритм описан почти везде, все баги словлены и описаны.
Так вот, я не могу реализовать двоичный поиск. Для меня он ни капельки не тривиален. Наверное, я ненастоящий программист. А ведь так и есть, я всего-лишь студент, но ведь это не оправдание? Если точнее, я не могу реализовать хороший корректный красивый двоичный поиск. Все время у меня вылезает проблема либо с корректностью, либо с красивостью, либо и с тем, и с другим. Так что, да, заголовок немного желтоват.
Прежде чем читать этот топик, напишите свою версию бинарного поиска — для отсортированного массива. Причем, в зависимости от параметра, поиск должен выдавать или первый элемент, или любой из дублирующих. Еще для сравнения, напишите бинарный поиск для функций
Для начала, я буду писать код на C#. Я надеюсь, поклонники других языков с легкостью поймут мой код. Границы поиска я буду представлять в виде полуинтервала [left; right), т.е. точка left включается, а точка right выключается. Для меня полуинтервалы удобнее, к их поведению я уже привык, кроме того, использование полуинтервалов имеет некоторые преимущества при программировании различных алгоритмов (о чем мы поговорим позже). Вообще, использовать полуинтервалы более правильно с точки зрения поддержки «единого стиля программирования», так как я пишу циклы вот так:а не так:
Я буду писать одновременно рекурсивную и итеративную версию, но мне ближе рекурсивная, так что не обессудьте. Для рекурсивной версии мы сделаем вот такую вот красивую обертку:
Первая попытка
Кстати, теперь можно добавить еще одну причину к использованию полуинтервалов: если у нас есть интервал [left, right], то мы должны его разбить на [left, mid — 1] и [mid + 1; right] (что конечно, чуть проще для запоминания, но весьма странно).
У полуинтервалов различие в индексах равно 1 (одному элементу, который мы выбрасываем), а у интервалов — 2 — магической цифре, взятой с потолка.
Особенно это заметно для сортировки слиянием, где для полуинтервалов различия в индексах нету (массив делится на [left, mid) и [mid, right)), а для интервалов появляется различие равное 1 (так как массив делится на [left, mid] и [mid + 1, right], или [left, mid — 1] и [mid, right]).
Теперь, осталось определить, в какой части массива нужно искать элемент, в зависимости от того, меньше ли средний элемент (array[mid]), чем ключ (key). Сделать это весьма просто — нужно просто подставить сначала один знак, проверить, работает ли программа, а если не работает, то другой :-). Почему-то именно такой способ проверки я и использую. Мне постоянно кажется, что перекомпилировать быстрее, чем «подумать».
Рекурсивно:
Итеративно:
Разбор полетов:
Если внимательно вчитаться в итеративную версию программы, то сразу становится понятно, что если элемента нет, то алгоритм никогда не остановится. Пониманию этого факта очень способствует while(true), которого в рекурсивной версии программы, естественно нет. И хотя я написал кучу реализаций рекурсивных алгоритмов, я все еще иногда сталкиваюсь с тем, что забываю остановить рекурсию. Как можно написать итеративную версию с подвохом, я не знаю.
Вторая попытка
Кстати, останавливать рекурсию мы будем в случае left == right, т.е., когда интервал стал таким — [left, right). Ну или в случае, когда right — left key
Т.е. если флаг descendingOrder не установлен, то выбор идет как обычно, если установлен, то выбор идет наоборот. Но это «хак», и возможно, что нужно написать какой-нибудь комментарий. Я не знаю, что именно он должен содержать.
Рекурсивно:
Итеративно:
Разбор полетов:
На всякий случай: один из вариантов проверки направления сортировки не учитывал, что массив может быть пуст. Я решил не выделять этот фейл в отдельную попытку.
Попытка №4
Дабы мы не попали на еще одну попытку, сразу скажу, что теперь рекурсию нужно останавливать еще и в случае, когда самый первый элемент из полуинтервала равен ключу. Ну а в случае, когда мы узнали, что средний элемент равен ключу у нас есть два варианта. Либо средний следует за первым и нужно выдавать именно его, ибо первый не равен ключу, поскольку рекурсия еще не остановилась. Либо нужно укорачивать область поиска (см. картинку выше)
Бинарный поиск в JavaScript. Практический пример
Что такое бинарный поиск?
Когда нужно выполнить поиск в массиве, простейшим способом может быть использование indexOf() или, возможно, цикла for(). Любой из этих способов будет начинать перебирать массив начиная с начала и переходить по каждому элементу массива до тех пор, пока не будет найдено нужное значение.
Теперь сравним это с бинарным поиском.
Бинарный поиск позволяет выполнять поиск в отсортированном массиве путем многократного разбиения массива пополам.
Бинарный поиск выполняется путем проверки того, является ли искомое значение больше, меньше или равно среднему значению в нашем массиве:
При работе с большими объемами данных гораздо эффективнее использовать бинарный поиск, поскольку при каждой итерации удаляется половина ненужных значений массива, а не только одно неподходящее значение.
Проект
Одним из наиболее важных аспектов диаграммы является подсказка, отображающая соответствующие данные при наведении курсора на диаграмму. При перемещении мыши на подсказке обновляются данные из ближайшей точки диаграммы. Пример:
У нас есть массив всех координат и соответствующих им данных. Координаты находятся внутри объекта, и каждый объект имеет svgX ключ. Выглядит это примерно так:
Изначально я использовал простой цикл for, чтобы сравнить текущую координату X курсора мыши со всеми значениями svgX в моем массиве данных.
Вот как выглядит код цикла for. Мы перебираем все значения svgX, и объект со значением, которое ближе к координате X курсора мыши — это тот объект, данные которого мы хотим показать.
Сначала мы получаем ширину нашего svg элемента и создаем пустой объект для хранения нашей ближайшей точки.
Затем мы перебираем массив данных. Каждое svgX значение объекта в нашем массиве сравнивается с координатой X курсора мыши. Если текущая итерация цикла имеет значение ближе к курсору, чем любая другая итерация, то эта точка устанавливается как наша ближайшая точка.
При небольшом количестве данных этот метод является относительно быстрым. Однако, если у нас есть большой объем данных, этот вариант уже не будет таким эффективным.
Бинарный поиск
Ниже приведен пример кода бинарного поиска для поиска ближайшего значения:
Нам нужно пять основных составляющих для нашего бинарного поиска:
Как видно из приведенного выше кода в строке 10, при запуске бинарного поиска мы передаем на вход весь массив данных, объект мыши, начальную позицию 0 и конечную позицию, равную полному размеру массива: 
Когда у нас есть наши данные, середину массива найдем путем деления на два, суммы из начальной и конечной позиций. Чтобы не получить дробь, результирующее число округляется вниз:
Таким образом, середина 0 + (4-0)/2 округленная вниз = 2: 
Мы помним, что для этого примера наше целевое значение равно 3,7. После того как мы нашли среднюю позицию, мы проверяем, равна ли она нашему целевому значению. Если это так, мы возвращаем объект, и все готово!
К сожалению, среднее значение массива = 3. А нашей целью является 3,7.
Далее мы проверим, совпадает ли наша конечная позиция — 1, с нашей начальной позицией:
Это условие сработает, когда наш массив уменьшился до двух финальных значений, и наша цель находится между ними. В этом случае мы возвращаем ближнее значение.
На текущей итерации условие вернет false.
Далее мы проверяем, больше ли наше целевое значение за среднее:
Это наш случай! Целевое значение 3,7 больше чем среднее 3. Мы можем избавиться от первых двух значений в нашем массиве:

Используя рекурсию мы возвращаем новый вызов функции binarySearch(). Передаем в функцию наш массив, целевое значение 3,7, среднее значение в качестве начальной позиции и конечное значение в качестве конечной позиции.
Наш новый вызов binarySearch(), будет искать от позиции 2 до data.length-1:

Функция находит новую среднюю позицию data[3]: 
Поскольку наше целевое значение 3,7 меньше среднего значения 4, мы отбрасываем правую сторону массива и возвращаем новый вызов функции binarySearch(). На этот раз наша начальная позиция остается data[2], а конечная позиция меняется на среднюю data[3]. 
Мы дошли до момента, когда наше условие выполнится:
Поскольку наше конечное значение минус единица равняется нашему начальному значению, мы знаем, что целевое значение находится где-то между ними. Мы должны возвратить элемент массива, значение которого ближе к значению 3,7. Поскольку 4 (конечное значение) ближе, то соответственно мы и возвращаем соответствующий элемент: data[3].
Тест скорости
Если объем данных небольшой, рекурсия может быть медленнее, чем цикл for. При тестировании на jsperf с 10 элементами, рекурсивная функция в среднем на 3% медленнее, чем цикл for. Однако при количестве элементов в 10 000, цикл for на 72% медленнее, чем рекурсивная функция. Это означает, что рекурсия практически в два раза быстрее, чем цикл for, и это огромная экономия времени!
Надеюсь, теперь вам понятны основы бинарного поиска в JavaScript!